Algèbre géométrique - Définition

Équation du second degré

Introduction par l'exemple

Calcul de la section d'or à l'aide d'un gnomon

À l'époque de Pythagore, il est probable que les grecs savaient construire rigoureusement un pentagone régulier. A priori, cette construction semble ne concerner que la géométrie, et c'est ainsi que les grecs le concevaient. Une lecture moderne indique que cette question est intimement liée à la résolution d'une question algébrique, à savoir la résolution d'un problème du second degré.

Le théorème de Pythagore permet la construction de φ

Construire cette figure suppose la connaissance des proportions du triangle isocèle formé par deux cotés adjacents du pentagone. Si l'on choisit l'unité égale à la longueur d'un coté et si φ désigne la base du triangle, qui correspond à une diagonale du pentagone, la proportion s'exprime de la manière suivante :

Du point de vue grec sous la forme (1), la question posée est géométrique, c'est celle de la détermination d'une proportion, qu'Euclide appelle d'extrême et de moyenne raison. Du point de vue moderne et sous la forme (2), la question posée est algébrique, c'est celle de la résolution d'une équation du second degré ayant pour unique solution positive le nombre d'or. Il est possible qu'Hippase de Métaponte, l'auteur probable de la construction, ait utilisé une méthode importée de Babylone, une fois encore à base d'un gnomon.

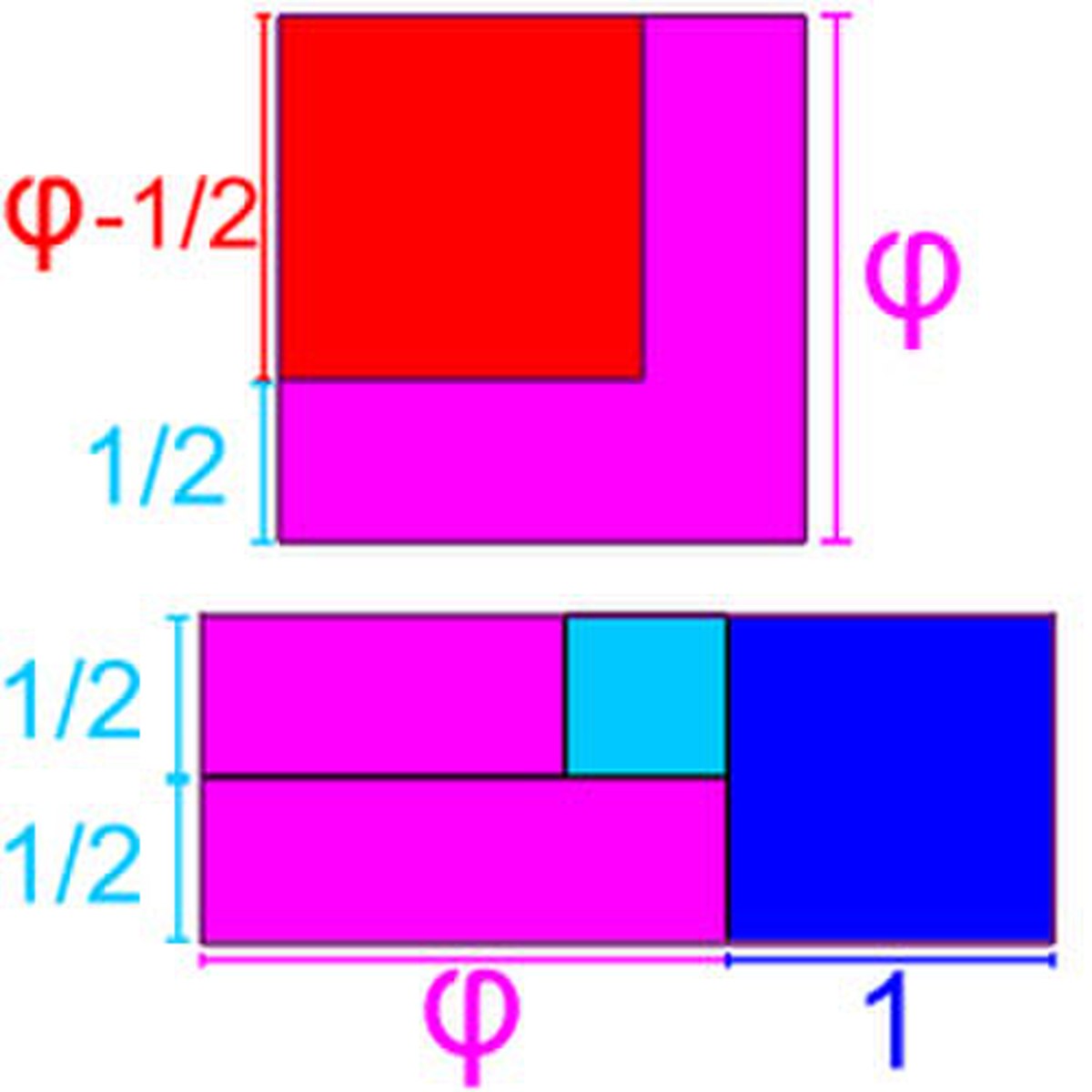
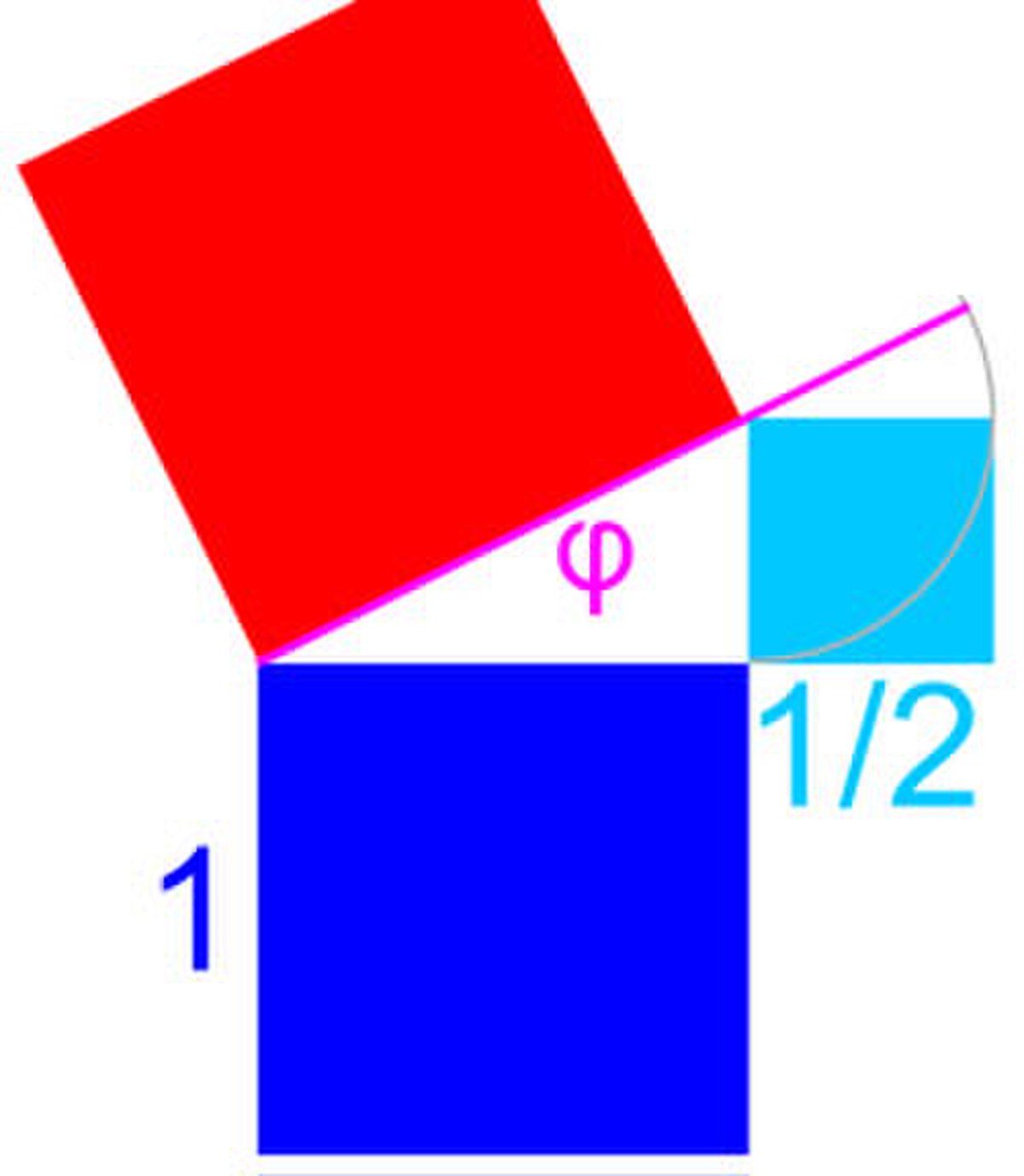
L'égalité φ² = φ + 1 directement issue de l'égalité (1) se lit de la manière suivante : un carré de côté φ possède la même aire qu'un rectangle de base φ + 1 et de hauteur 1, résultat représenté sur la figure de gauche. En retranchant au carré et au rectangle, l'aire d'un gnomon du hauteur φ et de largeur 1/2, on remarque qu'un carré de coté φ - 1/2 possède une aire égale à la somme de celle d'un carré de coté 1 et de celle d'un carré de coté 1/2. Obtenir la longueur φ devient aisé avec le théorème de Pythagore, elle est construite sur la figure de droite.

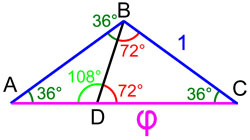
Soit ABC trois sommets consécutifs d'un pentagone régulier de cotés de longueur 1. Un polygone convexe de n cotés a, pour valeur de la somme de ses angles, (n - 2) x 180°, soit pour un pentagone 540°. Comme celui étudié ici est régulier, l'angle ABC est de mesure 540° / 5 = 108°. Les deux autres angles BCA et CAB sont égaux car le triangle est isocèle. Comme la somme des mesures des angles d'un triangle est égale à 180°, les deux autres angles ont pour mesure 36°. On obtient le triangle de la figure de droite.

Si l'on trace la droite passant par B et divisant l'angle ABC de 108° en deux angles comme sur la figure de droite, l'un de 36° et l'autre de 72°, on divise le triangle initial en deux triangles isocèles ABD et DBC. Une analyse des angles montre que le triangle ABC est semblable au triangle ABD. Il est alors possible d'appliquer le théorème de Thales en remarquant que AB = 1, AC = AD + DC = φ et BC = CD = 1 car le triangle DBC est isocèle. Finalement : AD = φ - 1, et l'on obtient :

 

Identité remarquable

Certaines identités remarquables se démontrent à l'aide de la géométrie plane.

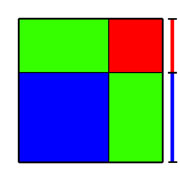
La résolution d'une équation du second degré, dans le cas général, se résout à l'aide de trois identités remarquables, développant les expressions (a + b)², (a - b)² et (a + b)(a - b). Elles se démontrent à l'aide des propriétés algébriques de l'addition et de la multiplication. Pour les grecs, ces résultats sont des vérités géométriques, qui se démontrent à l'aide d'un carré, en bleu sur la figure de droite et d'un gnomon, en vert et rouge.

Pour établir la formule suivante, on considère la figure de droite :

La longueur bleue représente a et la rouge b. L'expression (a + b)² est égale à l'aire du grand carré de côté a + b. Il est possible de le décomposer en trois partie : la zone bleu, correspondant à un carré de côté a et d'aire a²; la zone rouge, correspondant à un carré de côté b et d'aire b² et la zone verte, correspondant à deux rectangle de longueur a et de largeur b. Chaque rectangle de la zone verte est d'aire égale à a.b, la zone verte est d'aire 2ab. On retrouve bien l'identité remarquable (1).

On établit de même l'identité :

Cette fois ci, la longueur bleue désigne a - b et la rouge b. L'expression (a - b) correspond maintenant à l'aire du carré bleu. L'aire du carré bleu peut être vue comme la différence entre le grand carré, maintenant de côté a et les deux zones vertes et la zone rouge. Le rectangle composé d'une zone verte et du carré rouge a pour aire a.b. Si l'on retranche à l'aire du carré de côté a deux aires d'un rectangle de longueur a et de largeur b, on trouve l'aire du carré bleu ôtée de celle du carré rouge, ce qui donne l'identité suivante, dont on déduit une égalité équivalente à (2) :

L'identité (3) se démontre à l'aide de la même figure :

On utilise les mêmes conventions que celles établissant l'identité (2). L'aire de la surface a² - b² correspond à l'aire du grand carré ôtée de l'aire du carré rouge, c'est-à-dire à l'aire du carré bleu additionnée à l'aire des deux rectangles verts. Le rectangle composée de la zone bleue et d'une zone verte correspond à un rectangle d'aire a(a - b). Si l'on déplace un des deux rectangles verts pour le positionner de long du deuxième rectangle vert de manière à former un nouveau rectangle, on trouve un rectangle de longueur (a + b)(a - b). Ce rectangle est d'aire égale à celle du grand carré ôtée de l'aire du carré rouge, ce qui démontre l'identité (3).

Ainsi, toutes les identités remarquables utilisées pour résoudre des équations du second degré s'interprètent et se démontrent de manière géométrique. En conséquence, toutes les équations du second degré peuvent se résoudre de manière géométrique. Cette lecture, démontrant l'équivalence du contenu mathématique des identités remarquables avec un savoir géométrique présent dans le Livre II des Éléments d'Euclide est l'oeuvre de Zeuthen.

Résolution d'une équation du second degré

On recherche à résoudre l'équation suivante :

La méthode s'inspire directement de calculs analogues à ceux permettant d'établir les identités remarquables. Elle est illustrée sur la figure ci-dessous.

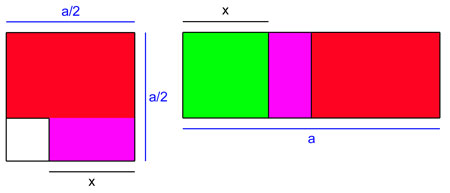
Dans un premier temps, on construit un carré de côté a/2. par hypothèse, ce carré est d'aire plus grande que c. On retranche au carré, en bas à gauche un petit carré de telle manière que la surface rouge et violette soit d'aire exactement égale à c.

Dans un deuxième temps, on remarque que la longueur x obtenue est aussi la hauteur du rectangle rouge de gauche. Il est donc possible de déplacer la zone violette sur la figure de droite et d'ajouter à gauche de cette figure un carré de côté x. L'aire rouge et violette est, d'après la construction de la figure de gauche, égale à c. Par construction, la figure de droite est d'aire égale à c + x². Cette aire est aussi égale à a.x, car la figure est un rectangle de base a et de hauteur x, ce qui donne la solution de l'équation. Ce mode de résolution provient directement du livre II des éléments d'Euclide.