Algèbre de Lie - Définition
La liste des auteurs de cet article est disponible ici.
Classification
Si
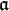
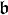
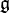
![[\mathfrak{a},\mathfrak{b}]](https://static.techno-science.net/illustration/Definitions/autres/c/c528d5c197e3f72db0a9bbc760333ee4_ecd7c90e0526368033da0c30c4758e97.png)
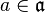
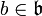
Algèbres de Lie nilpotentes
Une algèbre de Lie est dite nilpotente lorsque toute suite de commutateurs
![[[[g_1,g_2],g_3],\dots,g_n]](https://static.techno-science.net/illustration/Definitions/autres/4/48ab7757f1f2f8ed370a0f9d8acecd13_4ebd422ca442552a86478bd80e5fbe38.png)
Plus précisément, définissons Ci par
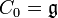
![C_{i+1}=[C_i,\mathfrak{g}]](https://static.techno-science.net/illustration/Definitions/autres/3/3b21f80fad4a73cdcc2c55569abfd0d0_9f579f9698b245a72ffd4b75292c77e4.png)
S'il existe un i tel que Ci=0, on dit que
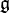
L'algèbre
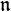

Le théorème d'Engel affirme que toute sous-algèbre nilpotente de
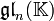
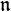
Algèbres de Lie résolubles
Définissons par récurrence Di par
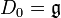
S'il existe un i tel que Di=0, on dit que
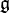
Un exemple d'algèbre de Lie résoluble est donné par l'algèbre
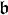
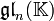
Le théorème de Lie montre que, si
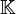
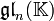
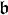
Algèbres de Lie semi-simples et réductives
On dit qu'une algèbre de Lie
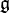
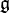
Lorsque
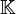
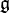
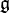
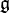
![[\mathfrak{g},\mathfrak{g}]](https://static.techno-science.net/illustration/Definitions/autres/3/3f1683bcf0fa96e29329efca70a1d284_7e7f2fc8ad66a04c3474bbea1cb1de08.png)
On peut montrer que, sous les mêmes hypothèses, toute algèbre de Lie semi-simple est en fait une somme directe d'algèbres de Lie simples.
Les algèbres de Lie simples de dimension finie sur le corps
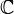
- À un diagramme de Dynkin de type
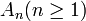
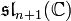
- À un diagramme de Dynkin de type
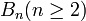
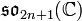
- À un diagramme de Dynkin de type
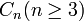
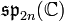
- À un diagramme de Dynkin de type
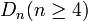
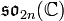
- Les algèbres de Lie exceptionnelles, correspondant aux diagrammes de Dynkin restants (de type E6, E7, E8, F4 et G2) n'ont pas d'interprétation aussi simple.
L'algèbre de Lie
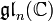
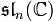
Les algèbres de Lie semi-simples de dimension finie sur le corps

- Les algèbres de Lie compactes. Ce sont les algèbres de Lie de groupes compacts. Il y en a exactement une qui correspond à chaque algèbre de Lie complexe.
- Les algèbres de Lie complexes vues comme algèbres de Lie réelles.
- Les autres peuvent être classées en familles AI, AII, AIII, BI, CI, CII, DI, DIII et en algèbres exeptionelles
EI, EII, EIII, EIV (de type E6) EV, EVI, EVII (de type E7) EVIII, EIX (de type E8) FI, FII (de type F4) et GI (de type G2) suivant la notation d'Helgason)
Dimension infinie
Il n'y a pas de classification générale des algèbres de Lie de dimension infinie mais plusieurs classes de telles algèbres ont été étudiées.
- Une algèbre de Kac-Moody est une algèbre de Lie définie abstraitement en termes de générateurs et relations codés par une matrice de Cartan généralisée non nécessairement définie positive. Elles peuvent donc être de dimension infinie. Leur classification générale est encore hors de portée mais plusieurs sous-types sont connus
- Une algèbre de Kac-Moody affine possède la propriété que tous les sous-diagrammes de Dynkin de son diagramme de Dynkin correspondent à des sous-algèbres de Lie de dimension finie. Sa matrice de Cartan généralisée est alors de corang 1. Les algèbres de Kac-Moody affines ont été classifiées par Victor G. Kac. Elles sont très utilisées en physique théorique dans l'étude des théories conformes des champs et en particulier dans l'étude des modèles WZW.
- Une algèbre de Kac-Moody hyperbolique possède un diagramme de Dynkin connexe avec la propriété que si on lui retire une racine, on obtient une algèbre de Lie semi-simple de dimension finie ou bien une algèbre de Kac-Moody affine. Elles ont été également classifiées et sont de rang 10 au maximum. Leur matrice de Cartan généralisée est non dégénérée et de signature Lorentzienne (c’est-à-dire avec exactement une direction négative).
- algèbre de Kac-Moody généralisée ou algèbre de Borcherds: c'est un type d'algèbre de Lie généralisant le concept d'algèbre de Kac-Moody dont la matrice de Cartan généralisée peut posséder des racines simples nommées imaginaires pour lesquelles l'élément diagonal de la matrice de Cartan généralisée est négatif. Elles ont été introduite par Richard Ewen Borcherds dans le cadre de l'étude de la conjecture moonshine.

















































