Algèbre de Clifford - Définition
La liste des auteurs de cet article est disponible ici.
Structure des algèbres de Clifford
Dans cette partie, nous supposons que l'espace vectoriel V est de dimension finie et que la forme bilinéaire de Q est non-dégénérée. Une algèbre centrale simple sur K est une algèbre de matrices sur une algèbre de division (de dimension finie) avec un centre K. Par exemple, les algèbres centrales simples sur les réels sont les algèbres de matrices sur soit les réels, soit les quaternions.
- Si V possède une dimension paire, alors
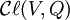est une algèbre centrale simple sur K. - Si V possède une dimension paire, alors
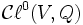est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes. - Si V possède une dimension impaire, alors 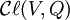est une algèbre centrale simple sur une extension quadratique de K ou sur une somme de deux algèbres centrales simples sur K isomorphes.
- Si V possède une dimension impaire, alors 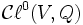est une algèbre centrale simple sur K.
La structure des algèbres de Clifford peut être établie explicitement en utilisant le résultat suivant. Supposons que U possède une dimension paire et une forme bilinéaire non-singulière avec un discriminant d, et supposons que V est un autre espace vectoriel avec une forme quadratique. L'algèbre de Clifford de U+V est isomorphe au produit tensoriel des algèbres de Clifford de U et 
, qui est l'espace V avec sa forme quadratique multiplié par 
. Sur les réels, cela implique en particulier que
Ces formules peuvent être utilisées pour trouver la structure de toutes les algèbres de Clifford réelles;
Spineurs
Supposons que p+q=2n est pair. Alors l'algèbre de Clifford 
est une algèbre de matrices, et donc possède une représentation complexe de dimension 
. En restreignat au groupe Pinp,q(R) nous obtenons une représentation complexe du groupe Pin de même dimension, appelé la représentation de spin. Si nous restreignons ceci au groupe de spin Spinp,q(R) alors il se sépare en une somme de deux représentations de demi-spin (ou représentations de Weyl ) de dimension 
.
Si p+q=2n+1 est impair alors l'algèbre de Clifford est une somme de deux algèbres de matrices, chacune d'elles possède une représentation de dimension , et celles-ci sont aussi toutes deux des représentations du groupe de Pin Pinp,q(R). Sur la restriction au groupe de spin Spinp,q(R), celles-ci deviennent isomorphes, donc le groupe de spin possède une représentation de spin complexe de dimension .
Plus généralement, les groupes de spin et les groupes de pin sur tout corps ont des représentations similaires dont la structure exacte dépend de la structure des algèbres de Clifford correspondantes : toutes les fois qu'une algèbre de Clifford possède un facteur qui est une algèbre de matrice sur certaines algèbre de division, nous obtenons une représentation correspondante des groupes de spin et de pin sur cette algèbre de division. Pour des exemples sur les réels :
Spin et groupes de Pin
Dans cette partie, nous supposons que V est de dimension finie et sa forme bilinéaire non-singulière. (Si K est de caractéristique 2, ceci implique que la dimension de V est pair).
Le groupe de Pin PinV(K) est le sous-groupe du groupe de Clifford 
d'éléments de norme de spin 1, et de manière similaire le groupe de Spin SpinV(K) est le sous-groupe d'éléments d'invariant Dickson 0 dans PinV(K). Lorsque la caractéristique n'est pas 2, ceux-ci sont les éléments de déterminant 1. Le groupe de Spin possède généralement un index 2 dans le groupe de Pin.
Rapellons, à partir de la partie précédente, qu'il existe un homomorphisme à partir du groupe de Clifford sur le groupe orthogonal. Nous définissons le groupe spécial orthogonal comme étant l'image de 
. Si K n'est pas de caractéristique 2, ceci est simplement le groupe d'éléments du groupe orthogonal de déterminant 1. Si K est de caractéristique 2, alors tous les éléments du groupe orthogonal sont de déterminant 1, et le groupe spécial orthogonal est l'ensemble d'éléments d'invariant de Dickson 0.
Il existe un homomorphisme à partir du groupe de Pin vers le groupe orthogonal. L'image est constituée des éléments de norme de spin 1 ∈ K*/K*2. Le noyau est constitué des éléments +1 et -1, et est d'ordre 2 à moins que K soit de caractéristique 2. De manière similaire, il existe un homomorphisme à partir du groupe de Spin vers le groupe spécial orthogonal de V.
Dans le cas courant, lorsque V est un espace défini positif ou négatif sur les réels, le groupe de spin s'applique sur le groupe spécial orthogonal, et est simplement connexe lorsque V est de dimension au moins égale à 3. Attention : Ceci n'est pas vrai en général : si V est 
pour p et q tous deux au moins égal à 2, alors le groupe de spin n'est pas simplement connexe et ne s'applique pas sur le groupe spécial orthogonal. Dans ce cas, le groupe algébrique Spinp,q est simplement connexe comme un groupe algébrique, quoique sont groupe de points à valeurs réelles Spinp,q(R) n'est pas simplement connexe. Ceci est plutôt un point subtil, qui a complètement embrouillé les auteurs d'au moins un livre sur les groupes de spin.
Voir groupe spineur, spineur.