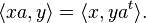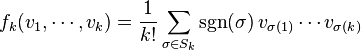Algèbre de Clifford - Définition

Construction et propriété universelle

Soit V un espace vectoriel sur un corps K, et une forme quadratique sur V. Une algèbre de Clifford est une algèbre associative unitaire sur K munie d'une application linéaire définie par la propriété universelle suivante :

Pour toute algèbre associative A sur K munie d'une application linéaire vérifiant j(v)² = Q(v)1 pour chaque vecteur v de V (où 1 désigne le neutre multiplicatif de A), il existe un unique homomorphisme d'algèbres faisant commuter le diagramme suivant :

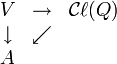
c'est-à-dire que .

En travaillant avec la forme bilinéaire symétrique associée à Q (de caractéristique différente de 2), la condition sur j est

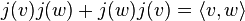pour tout v w ∈ V.

Une algèbre de Clifford comme décrite ci-dessus existe toujours et peut être construite comme suit : Démarrer avec l'algèbre la plus générale qui contient V, concrètement l'algèbre tensorielle T(V), puis imposer l'identité fondamentale en prenant un quotient convenable. Dans notre cas, nous voulons prendre l'idéal bilatère dans engendré par tous les éléments de la forme

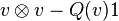pour tout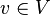

et définissons comme le quotient

.

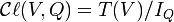Il est alors plus direct de montrer que contient V et satisfait la propriété universelle ci-dessus, donc que est unique à un isomorphisme près; ainsi on parle de l'algèbre de Clifford . Il suit aussi de cette construction que i est injective. Habituellement, on laisse tomber le i et on considère V comme un sous-espace vectoriel de .

Une conséquence de la définition est que pour tous vecteurs u,v de V, l'identité est vraie dans C(Q). Si le corps n'est pas de caractéristique 2, cette propriété peut être utilisée en tant que définition alternative.

La caractérisation universelle des algèbres de Clifford montre que la construction de est de nature fonctorielle. Concrètement, peut être considéré comme un foncteur issu de la catégorie des espaces vectoriels avec formes quadratiques (dont les morphismes sont des applications linéaires préservant la forme quadratique) vers la catégorie des algèbres associatives. La propriété universelle garantit que les applications linéaires entre les espaces vectoriels (préservant la forme quadratique) s'étendent de façon unique vers les homomorphismes d'algèbre entre les algèbres de Clifford associées.

Propriétés

Relation avec l'algèbre extérieure

Etant donné un espace vectoriel V, on peut construire l'algèbre extérieure , dont la définition est indépendante de toute forme quadratique sur V. Il s'avère que si F n'est pas de caractéristique 2 alors il existe un isomorphisme naturel entre et considéré comme des espaces vectoriels. C'est un isomorphisme d'algèbre si et seulement si Q = 0. On peut ainsi considérer l'algèbre de Clifford comme un enrichissement de l'algèbre extérieure sur V avec une multiplication qui dépend de Q.

La manière la plus facile d'établir l'isomorphisme est de choisir une base orthogonale {e_i} pour V et de l'étendre en une base orthogonale pour comme décrit ci-dessus. L'application est déterminée par

.

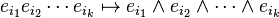Note : Ceci fonctionne seulement si la base {e_i} est orthogonale. On peut montrer que cette application est indépendante du choix de la base orthogonale et donc donne un isomorphisme naturel.

Si la caractéristique de K est 0, on peut aussi établir l'isomorphisme par antisymétrie. Définissons les fonctions par

où la somme est prise sur le groupe symétrique sur k éléments, et où sgn(σ) est la signature de la permutation σ. f_k est alternée, et induit une application linéaire unique . La somme directe de ces applications donne une application linéaire entre et . On peut montrer que cette application est un isomorphisme linéaire.

Une autre manière de voir la relation est la construction d'un filtre sur . Rappelons que l'algèbre tensorielle T(V) possède un filtre naturel : où F^k contient les sommes de tenseurs de rang ≤ k. Projeter ceci vers l'algèbre de Clifford donne un filtre sur . L'algèbre graduée associée

est naturellement isomorphe à l'algèbre extérieure .

Une manière plus simple est de voir qu'en choisissant une base de V, on peut toujours exprimer, grâce à la relation d'anticommutativité, un élément de l'algèbre de Clifford comme combinaison linéaire de monômes du type :

,

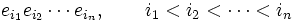ce qui donne un isomorphisme explicite avec l'algèbre extérieure. Notons que ce n'est qu'un isomorphisme d'espaces vectoriels.

Si V est de dimension finie paire, que le corps est algébriquement clos et que la forme quadratique est non dégénérée, l'algèbre de Clifford est centrale simple. Ainsi, par le théorème d'Artin-Wedderburn, elle est (non canoniquement) isomorphe à une algèbre de matrices. Il s'ensuit que dans ce cas, C(q) possède une représentation irréductible de dimension , qui est unique à un isomorphisme (non unique) près. C'est la (sulfureusement) célèbre représentation spinorielle, dont les vecteurs sont appelés spineurs.

Graduation

L'application linéaire sur V définie par conserve la forme quadratique Q et donc, par la propriété universelle des algèbres de Clifford s'étend à un automorphisme d'algèbre

.

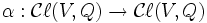Puisque est une involution (i.e. son carré est l'identité), on peut décomposer en deux espaces propres positifs et négatifs

où . Puisque est un automorphisme, il vient

où les indices supérieurs sont lus modulo 2. Ceci signifie que est une -algèbre graduée (aussi connue comme une superalgèbre).

Note : forme une sous-algèbre de , appelée la sous-algèbre paire. La partie est appelée la partie impaire de (ce n'est pas une sous-algèbre). Cette -graduation joue un rôle important dans l'analyse et l'application des algèbres de Clifford. L'automorphisme est appelé l'involution principale ou l'involution de grade.

Remarque. En caractéristique différente de 2, l'algèbre hérite d'une -graduation de l'isomorphisme canonique avec l'algèbre extérieure . Néanmoins, ceci est un espace vectoriel seulement gradué, c’est-à-dire que la multiplication de Clifford ne respecte pas la -graduation, seulement la -graduation. Heureusement, les graduations sont reliées d'une manière naturelle : . Le degré d'un nombre de Clifford fait référence généralement au degré dans la -graduation. Les éléments qui sont homogènes dans la -graduation sont simplement dits pairs ou impairs.

Si la caractéristique de K n'est pas 2, alors la sous-algèbre paire d'une algèbre de Clifford est elle-même une algèbre de Clifford. Si V est la somme directe orthogonale d'un vecteur a de norme Q(a) et un sous-espace U, alors est isomorphe à , où -Q(a)Q est la forme Q restreinte à U et multipliée par -Q(a). En particulier sur les réels, ceci implique que

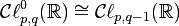pour q > 0 et

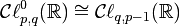pour p > 0.

Dans le cas défini négatif, cela donne une inclusion qui étend la suite

De même, dans le cas complexe, on peut montrer que la sous-algèbre paire de est isomorphe à .

L'algèbre de Clifford est filtrée par les sous-espaces constitués d'éléments pouvant être écrits comme monômes en 0, 1, 2 ... vecteurs de V. L'algèbre graduée associée est canoniquement isomorphe à l'algèbre extérieure de l'espace vectoriel. Cela montre en particulier que .

Anti-automorphismes

En plus de l'automorphisme , il existe deux anti-automorphismes qui jouent un rôle important dans l'analyse des algèbres de Clifford. Rappelons que l'algèbre tensorielle T(V) possède un anti-automorphisme qui renverse l'ordre de tous les produits :

.

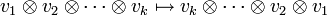Puisque l'idéal est invariant sous ce renversement, cette opération descend vers un anti-automorphisme de appelé l'opération de transposition ou de renversement, notée par . La transposition est un anti-automorphisme : . L'opération de transposition ne fait pas usage de la -graduation donc nous définissons un deuxième anti-automorphisme par composition d'α et la transposition. Nous appelons cette opération la conjugaison de Clifford notée

.

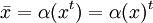De ces deux anti-automorphismes, la transposition est la plus fondamentale.

Note : Toutes ces opérations sont des involutions. On peut montrer qu'ils agissent comme ±1 sur les éléments qui sont homogènes dans la -graduation. En fait, toutes les trois opérations dépendent seulement sur le degré modulo 4. C’est-à-dire, si x est homogène avec un degré k, alors

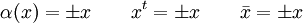où les signes sont donnés par la table suivante :

k mod 4	0	1	2	3
	+	-	+	-
	+	+	-	-
	+	-	-	+

Le produit scalaire de Clifford

Lorsque la caractéristique n'est pas 2, la forme quadratique Q sur V peut être étendue à une forme quadratique sur toutes les comme expliqué plus haut (et que nous avons aussi notée par Q). Une définition de base indépendante est

où <a> désigne la partie scalaire de a (la partie de graduation 0 dans la -graduation). On peut montrer que

où les v_i sont les éléments de V — cette identité n'est pas vraie pour des éléments arbitraires de .

La forme bilinéaire symétrique associée sur est donnée par

On peut vérifier que ceci se réduit à la forme bilinéaire originale lorsqu'elle est restreinte à V. La forme bilinéaire de toutes les est non dégénérée si et seulement si elle n'est pas dégénérée sur V.

Il n'est pas difficile de vérifier que la transposition est l'adjoint de la multiplication de Clifford gauche/droite avec le respect de ce produit intérieur. C’est-à-dire,

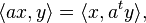et