Addition - Définition
La liste des auteurs de cet article est disponible ici.
Autres additions
Addition vectorielle
Vecteurs d'un espace affine
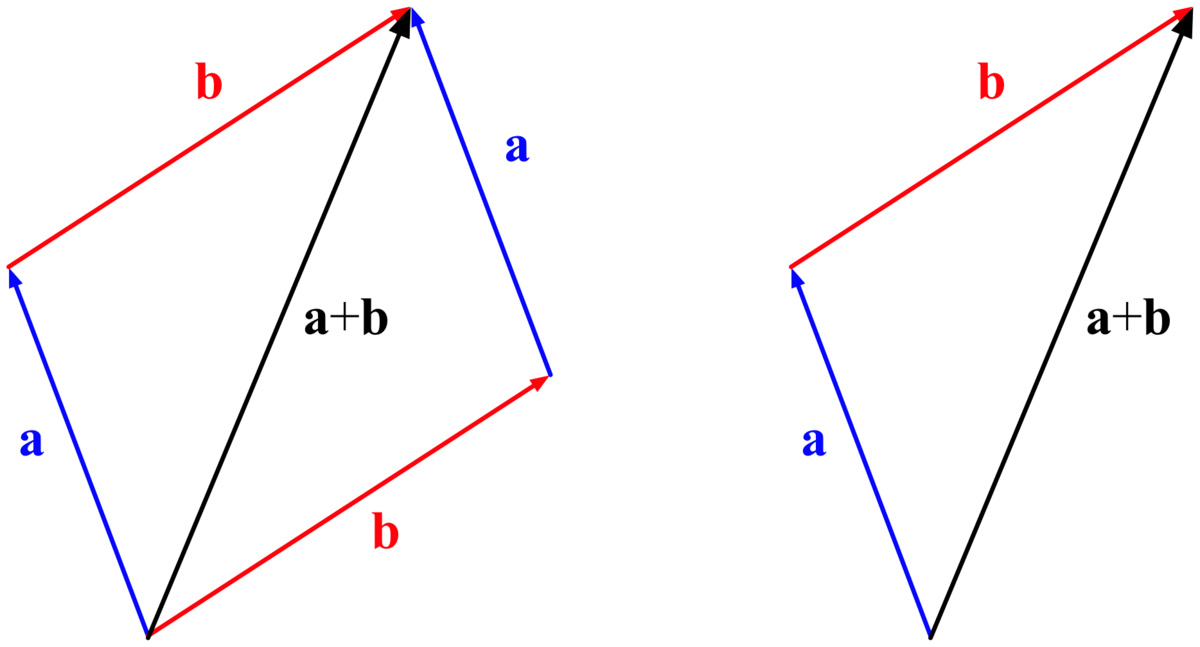
Étant donnés quatre points A, B, C, D d'un espace affine tel que le plan ou l'espace euclidien, l'addition des deux vecteurs
Le vecteur somme
L'addition de vecteurs satisfait toutes les propriétés de l'addition numérique. Son neutre est le vecteur nul et l'opposé d'un vecteur est un vecteur de même direction et même norme mais de sens opposé.
Lorsque les vecteurs sont définis sur une même droite munie d'un repère, l'addition des vecteurs s'identifie à celle des mesures algébriques.
Coordonnées et composantes
Les coordonnées des vecteurs dans un repère cartésien permettent de traduire l'addition vectorielle en une succession d'additions de nombres. En effet, si deux vecteurs du plan ont pour coordonnées respectives (x;y) et (x';y'), le vecteur somme aura pour coordonnées (x + x';y + y').
Dans l'espace usuel, l'addition est représentée par l'opération sur les triplets de coordonnées (x;y;z) + (x';y';z') = (x + x';y + y';z + z').
Le principe de l'addition terme à terme est repris pour d'autres structures mathématiques telles que l'ensemble des n-uplets de nombres et les suites :
Les matrices de même taille et les applications à valeur numérique s'additionnent également de cette manière.
Addition avec modulo
| + | 0 | 1 | 2 | 3 | 4 |
| 0 | 0 | 1 | 2 | 3 | 4 |
| 1 | 1 | 2 | 3 | 4 | 0 |
| 2 | 2 | 3 | 4 | 0 | 1 |
| 3 | 3 | 4 | 0 | 1 | 2 |
| 4 | 4 | 0 | 1 | 2 | 3 |
Puisque la parité d'une somme ne dépend que de la parité des opérandes, il peut être défini une addition sur les parités.
| + | pair | impair |
| pair | pair | impair |
| impair | impair | pair |
Cette opération se généralise pour tout entier strictement positif m en une addition modulo m sur les chiffres de 0 à m − 1, dans laquelle chaque nombre est remplacé par le reste de sa division euclidienne par m.
L'addition sur les parités est alors représentée par l'addition modulo 2, où les nombres pairs sont remplacés par 0 et les nombres impairs par 1.
Addition booléenne
L'addition booléenne est l'écriture du connecteur logique « OU » avec les chiffres 0 pour FAUX et 1 pour VRAI. Elle est donc donnée par la table d'addition suivante :
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
L'opération est associative et commutative, l'élément 0 est neutre mais l'élément 1 n'a pas d'opposé.
Addition géométrique sur une courbe cubique
Sur certaines courbes, on peut définir une addition géométriquement. C'est possible en particulier sur des courbes cubiques, c'est-à-dire des courbes planes définies par une équation du 3e degré. Plus précisément, en appelant x et y les coordonnées dans le plan réel, les points de la courbe sont les points P dont les coordonnées x,y vérifient une équation F(x,y) = 0, pour un polynôme F du troisième degré à coefficients réels donné. On suppose aussi que la courbe n'a pas de points singuliers, c'est-à-dire ici de points de rebroussement ou de points doubles ; la tangente est donc bien définie en chaque point. Pour uniformiser les constructions, on rajoute aussi un point à l'infini.
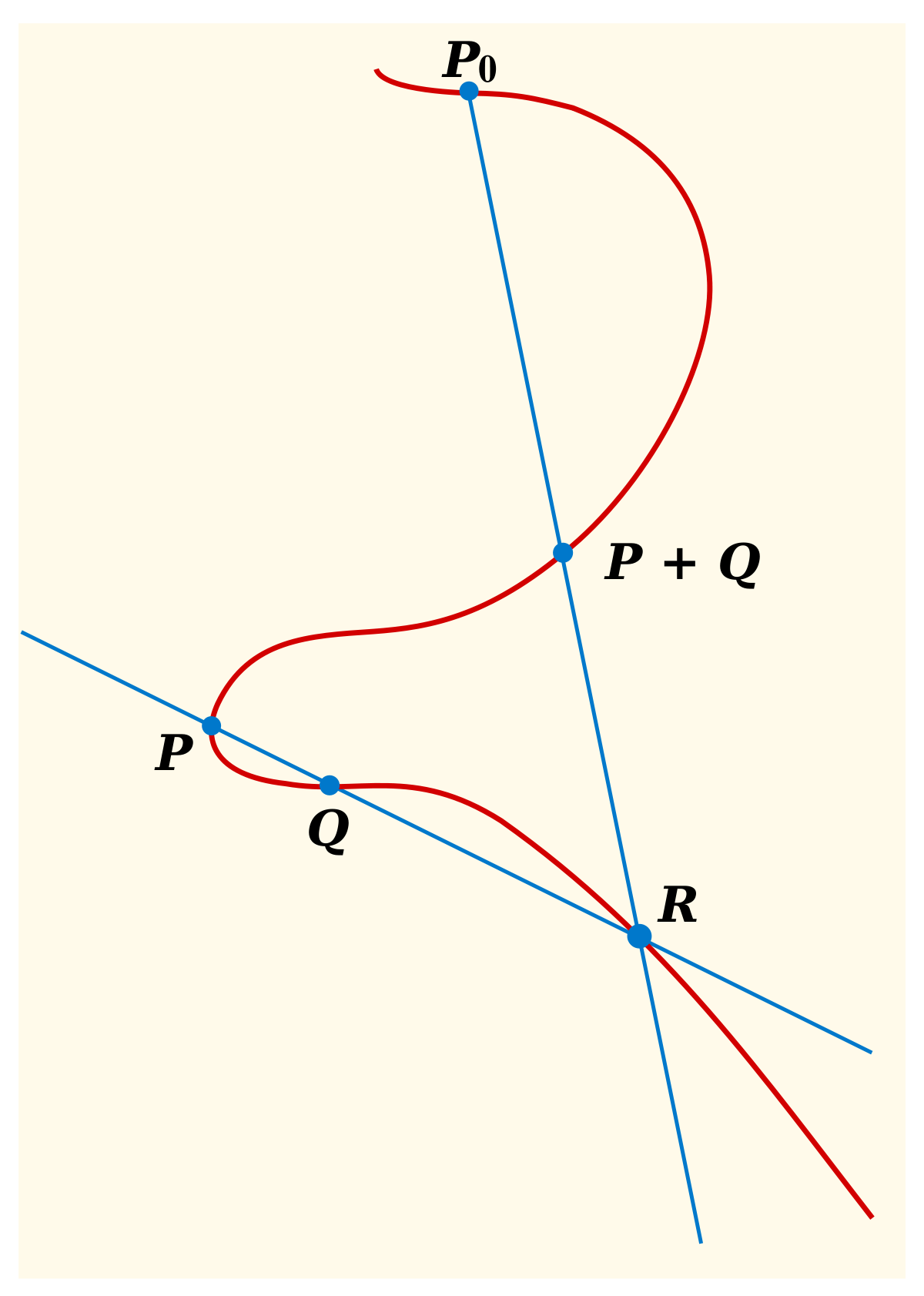
Soit maintenant deux points quelconques de la courbe, P et Q. La droite qui les joint recoupe la courbe en un troisième point R (si P = Q, on prend comme droite les joignant la tangente en P). Ce procédé définit bien une opération binaire sur la courbe. Elle n'a pas encore les propriétés attendues d'une addition : par exemple, il n'y a pas d'élément neutre. Pour y remédier, on fixe un point au choix sur la courbe, qu'on note P0, et on considère la droite passant par P0 et R : elle coupe encore la cubique en un troisième point. C'est ce point qu'on appelle 'somme de P et Q' (et on le note P + Q).
Le point choisi P0 est l'élément neutre (le 'zéro') pour cette opération. Quant à l' 'opposé' d'un point P, c' est le troisième point d'intersection avec la courbe de la droite passant par P et P'0, où P'0 est le troisième point d'intersection avec la courbe de la tangente à la courbe en P0.
