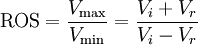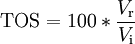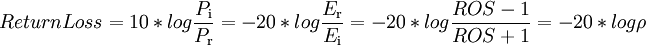Adaptation d'impédances - Définition

Adaptation des lignes de transmission en transmission du signal

Le problème général consiste à transmettre un signal depuis une source jusqu'à une charge (ou récepteur) distante de cette source. Le problème est résolu par l'utilisation d'une ligne de transmission entre cette charge et cette source. La source et la charge présentent en général une résistance interne R ( généralement R = 50 ohms pour les signaux RF, et R = 600 ohms pour les signaux audio...).

Le principe fondamental est le suivant : En connectant sur la charge de résistance R , une ligne de transmission d'impédance caractéristique R, on retrouvera à l'autre extrémité de la ligne la même résistance R. Autrement dit, la source et la charge de résistance R seront « adaptées » si la ligne qui les relie possède une impédance caractéristique de même valeur. L'adaptation sera conservée quelle que soit la longueur de la ligne.

Par contre, si la charge présente une résistance différente de l'impédance caractéristique de la ligne, on aura des phénomènes d'ondes stationnaires. On observera alors les phénomènes suivants :

- Les tensions et courants ne sont plus constants le long de la ligne : on a des « ondes stationnaires », ce qui induit plus de pertes dans la ligne.

- Une partie de l'énergie n'est plus absorbée par la charge : on a une perte de la puissance transmise à la charge.

- Si la longueur de la ligne n'est pas très petite par rapport à la longueur d'onde, la source ne verra plus une résistance fixe R , mais une impédance dépendant de la fréquence et de la longueur de la ligne. La courbe de réponse en fréquence de la ligne sera alors perturbée, ce qui peut être grave en téléphonie ou en transmission de données.

On peut quantifier ces perturbations par le rapport d'onde stationnaire (ROS, ou SWR/VSWR pour Voltage Standing Wave Ratio) :

avec V_i l'amplitude de l'onde incidente
V_r l'amplitude de l'onde réfléchie

On trouve aussi d'autres indicateurs : le Taux d'Onde Stationnaire

le Return Loss

avec

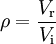
La mesure du ROS indique la désadaptation entre charge et ligne , et la perte de puissance associée.

À titre de données pratiques : Si une ligne d'impédance caractéristique 50 ohms est chargée par 100 ohms ou par 25 ohms, le ROS sera égal à 2, et le taux d'énergie réfléchie par la charge sera de 11 %.

Si la même ligne est chargée par 150 ohms ou par 16,6 ohms, le ROS sera de 3 et le taux d'énergie réfléchie par la charge sera de 25 %.

L'abaque de Smith permet de trouver l'impédance à l'extrémité d'une ligne de longueur donnée, chargée à l'autre extrémité par une impédance quelconque donnée.

Il est toutefois à remarquer que si la ligne qui alimente la charge dispose d'un dispositif d'adaptation d'impédance entre la source et l'entrée de la ligne, l'énergie réfléchie par la charge désadaptée est renvoyée en phase avec l'énergie incidente et n'est donc pas perdue, aux pertes en ligne près. Il finit par s'installer un régime d'ondes stationnaires tel que la ligne transporte une énergie incidente supérieure à l'énergie débitée par la source mais compensée par l'énergie réfléchie par la charge. Au total la charge utilise bien toute l'énergie de la source mais pas plus. Ceci implique que le dispositif de couplage au début de la ligne ne modifie pas le ROS en ligne ni à la charge. En cas de pertes en ligne, en parcourant celle-ci de la charge vers la source, le ROS s'améliore et si la ligne est très longue il peut même arriver à 1:1. Dans l'abaque de Smith, le parcours se visualise par une spirale qui tend vers le centre. En absence de pertes la spirale devient un cercle centré.