La física cuántica descubre "por accidente" una nueva representación de π (Pi)

Pi posee un número infinito de decimales no repetitivos.
Imagen de ilustración Pixabay
Bajo ciertas condiciones, esta nueva fórmula para π se acerca a la de Madhava, un matemático indio del siglo XV, quien fue el primero en proponer una serie para π. Los investigadores Arnab Saha y Aninda Sinha, del Centro de Física de Altas Energías (CHEP), han publicado sus trabajos en Physical Review Letters.
Inicialmente, Saha y Sinha no tenían el objetivo de encontrar una nueva representación de π. Su investigación se centraba en el estudio de las interacciones de partículas a alta energía, como las observadas en el Gran Colisionador de Hadrones, en el marco de la teoría de cuerdas. Esta teoría supone que los procesos cuánticos resultan de las vibraciones de cuerdas.
El equipo combinó dos herramientas matemáticas: la función Beta de Euler y el diagrama de Feynman. La función Beta de Euler interviene en varios campos de la física y la ingeniería, mientras que el diagrama de Feynman describe los intercambios de energía durante la interacción de partículas.
Esta aproximación no solo permitió modelar eficazmente las interacciones de partículas, sino que también llevó al descubrimiento de una nueva serie para representar π. En matemáticas, una serie permite descomponer un parámetro como π en sus componentes. La nueva serie permite aproximar rápidamente el valor de π, esencial para los cálculos de difusión de partículas a alta energía.
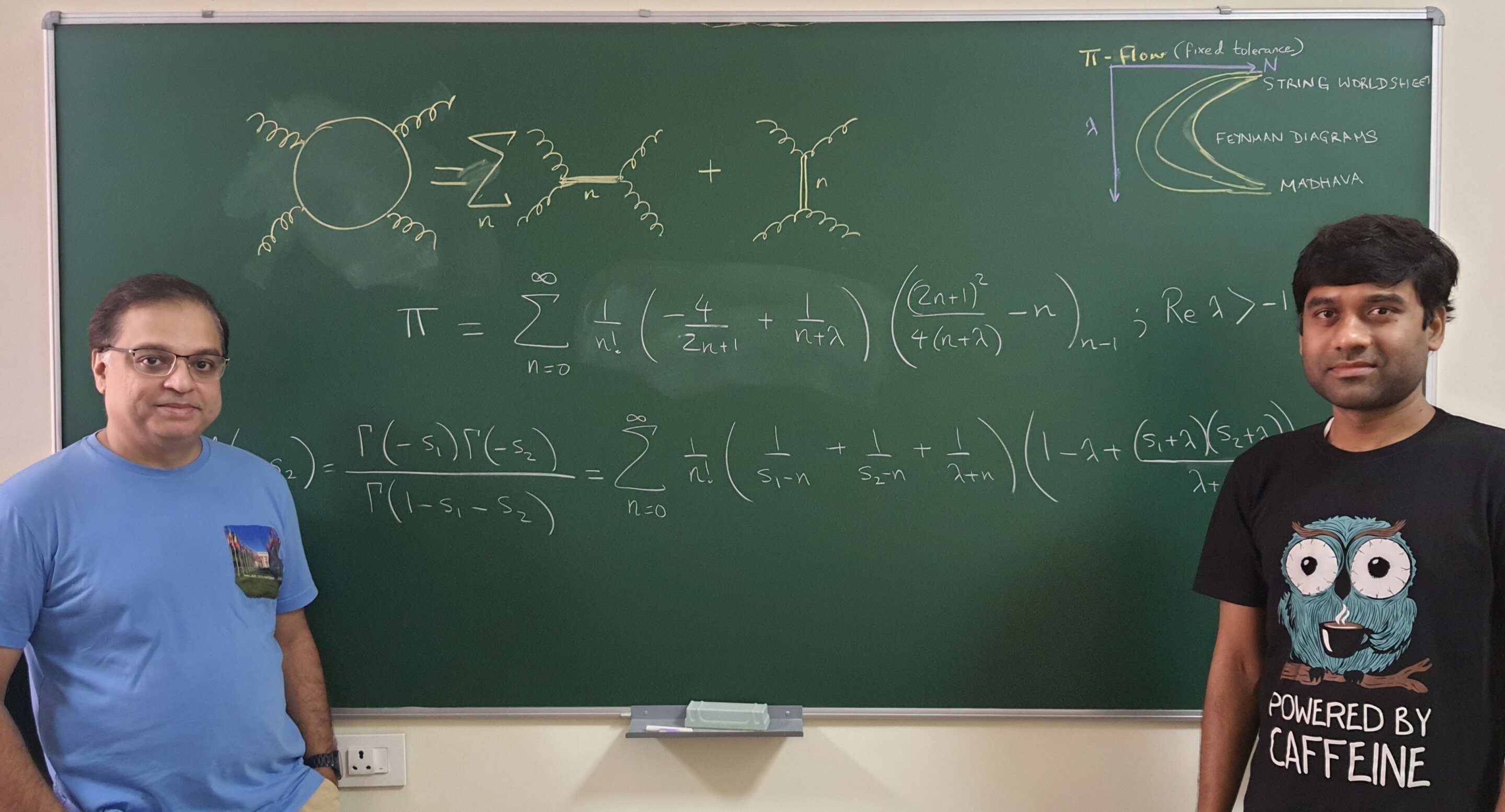
Aninda Sinha (izquierda) y Arnab Saha (derecha).
Crédito: Manu Y
Los investigadores explican que este resultado fue posible gracias a herramientas matemáticas modernas, ausentes en los primeros intentos de modelización en los años 70. Aunque estos trabajos siguen siendo teóricos, podrían, con el tiempo, tener aplicaciones prácticas, como los descubrimientos de Paul Dirac sobre los electrones que condujeron a tecnologías médicas avanzadas.
Sinha concluye subrayando que esta investigación, aunque pueda parecer alejada de las preocupaciones cotidianas, ofrece el puro placer de la teoría por la teoría.