Combinatoire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la combinatoire, appelée aussi analyse combinatoire, étudie les configurations de collections finies d'objets ou les combinaisons d'ensembles finis, et les dénombrements.
Généralités et historique
La combinatoire remonte à l'Antiquité : Plutarque rapporte ainsi un débat entre Chrysippe et Hipparque sur le nombre de façons de combiner dix propositions, le résultat n'ayant été compris qu'au XXe siècle. Parmi, les autres précurseurs, on peut citer Bhāskara II au XIIe siècle (nombre de choix de p éléments parmi n), Raymond Lulle au XIIIe siècle, Gersonide au début du XIVe siècle (rapport entre le nombre d'arrangements et le nombre de combinaison), Michael Stifel au XVIe siècle (première approche du triangle de Pascal). Elle se développe de façon significative à partir du XVIIe siècle, en même temps que le calcul des probabilités avec Blaise Pascal et Pierre de Fermat. Initialement, elle avait pour objet la résolution des problèmes de dénombrement, provenant de l'étude des jeux de hasard. Plus tard, elle se lia à la théorie des nombres et à la théorie des graphes.
En particulier, la combinatoire s'intéresse aux méthodes permettant de compter les éléments dans des ensembles finis (combinatoire énumérative) et à la recherche des optima dans les configurations ainsi qu'à leur existence (combinatoire extrémale).
Voici quelques exemples de situations donnant lieu à des questions d'analyse combinatoire :
- les rangements de livres sur une étagère ;
- les dispositions de personnes autour d'une table ronde ;
- les tirages avec remise d'un certain nombre de boules numérotées dans une urne ;
- les placements de jetons sur un damier.
Quel est le nombre d'ordonnancements possibles des cartes d'un jeu de 52 cartes ?
Ce nombre est égal à 52! (le « ! » dénotant la factorielle). Il peut sembler étonnant que ce nombre, environ 8,065817517094 ×1067, soit si grand. C'est environ 8 suivi de 67 zéros. Il est, par exemple, plus grand que le nombre d'Avogadro, égal à 6,022 ×1023.
Permutations (dispositions, ordonnancements)
Permutations sans répétition d'objets discernables
Les permutations sans répétition d'un ensemble fini E sont les bijections de E sur lui-même.
Comme exemple d'introduction, considérons le nombre de dispositions de six objets discernables dans six cases consécutives numérotées avec un et un seul objet par case. Chacun des objets peut être placé dans la première case, ce qui donne six possibilités d'occuper la première place. Une fois la première place occupée par l'un des objets, il reste encore cinq candidats pour la deuxième place, la deuxième place étant attribuée, il reste seulement quatre candidats pour la troisième place, et ainsi de suite. Pour l'avant-dernière place, il ne reste plus que deux objets, et une fois l'un des deux placé, la dernière place doit être occupée par le dernier objet.
Il y a ainsi 6 × 5 × 4 × 3 × 2 × 1 ou 6! = 720 possibilités de disposer six objets discernables.
- Généralisation
Nous allons voir que le nombre de dispositions de n éléments discernables est égal à n !
Une disposition des objets d'un ensemble E de cardinal n, dans n cases avec un et un seul objet par case, ou un ordonnancement des éléments de E se représente par une bijection de {1, 2, …, n} dans E ou une permutation de E. Il est commode de représenter une telle bijection par un n-uplet (ou n-liste) d'éléments de E, (x1, x2, …, xn).
- Théorème
Il y a n! permutations (sans répétition) de n éléments.
En effet, pour former un n-uplet d'éléments de E, nous devons choisir un élément de E pour la première place du n-uplet et il y a n possibilités, il y a n - 1 choix possibles d'un élément de E pour la deuxième place, n - 2 pour la troisième etc. Il n'y a plus qu'un seul choix d'élément pour la dernière place. Donc au total n × (n-1) × (n-2) × … × 2 × 1 permutations.
Cette propriété se démontre par récurrence sur n.
Permutations avec répétition d'objets discernables
Pour déterminer le nombre des dispositions possibles d'objets de plusieurs classes et mutuellement indiscernables dans chaque classe, il est utile de considérer le nombre de dispositions possibles de ces objets en les supposant tous discernables, et ensuite de trouver combien de ces dispositions sont indiscernables. Le nombre des dispositions possibles de ces objets est égal au nombre de dispositions possibles des objets considérés comme discernables divisé par le nombre des dispositions indiscernables.
Par exemple, si nous devons déterminer le nombre total de dispositions d'objets dont deux sont d'une première classe, trois d'une deuxième classe et cinq d'une troisième classe, alors nous calculons le nombre total de dispositions de ces objets considérés comme discernables, ce qui donne (2 + 3 + 5)!, soit 3 628 800 dispositions possibles. Mais certaines dispositions restent inchangées lorsque les objets indiscernables d'une même classe sont échangés mutuellement, et il y a 2! × 3! × 5! soit 1 440 façons de permuter les objets de chacune de ces classes.
Nous obtenons au total 3 628 800 ÷ 1 440 = 2 520 dispositions différentes. Il s'agit aussi du nombre de permutations avec répétition de 10 éléments avec 2, 3 et 5 répétitions.
- Généralisation
Le nombre de permutations de n éléments, répartis dans k classes dont n1 sont de classe 1, n2 sont de classe 2, …, nk sont de classe k, indiscernables dans chaque classe, ou le nombre de permutations de n éléments avec n1, n2, …, nk répétitions, avec 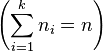 , est égal à :
, est égal à : ![]() .
.