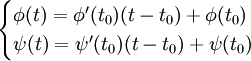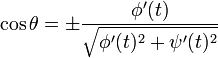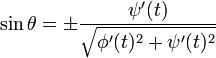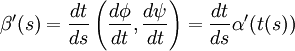Courbe plane - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

En géométrie, une courbe plane est une courbe qui est entièrement contenue dans un (unique) plan, et qui est identifiable à une fonction continue :

$\alpha: I \longrightarrow \R^2~$

où $I$ est un intervalle de l'ensemble $\R$ des nombres réels.

L'image d'une courbe est aussi appelée support de la courbe. Parfois, on utilise aussi l'expression courbe pour indiquer le support d'une courbe. Une courbe sur un espace euclidien de dimension supérieure à 2 est dite plane si son support est contenu dans un plan lui-même contenu dans l'espace euclidien dans lequel elle est définie.

Une courbe plane est dite simple si elle ne se recoupe pas, autrement dit, si

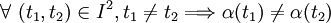$\forall \ (t_1,t_2) \in I^2, t_1 \ne t_2 \Longrightarrow \alpha(t_1) \ne \alpha(t_2)$ .

Représentations

Représentation par une forme cartésienne explicite

Une manière de représenter une courbe plane est l'équation :

$y = f(x)\,$

telle qu'à chaque point x corresponde un point y, et de façon à ce que chaque point du plan xy : (x,y) représente le support de la courbe. Une courbe de ce type est également nommée graphique en référence au graphique d'une fonction réelle ; en effet, la représentation peut aussi s'écrire :

$\alpha (t) = (t,f(t))\,$

c'est-à-dire comme fonction d'une variable indépendante. Cette représentation a de nombreuses limites géométriques, du fait que très souvent, une courbe a une description très complexe sous cette forme, qui n'est donc pas adaptée à l'étude des propriétés géométriques.

Représentation par une forme cartésienne implicite

Une courbe peut également être représentée sous la forme :

$F(x,y)=0\,$

c'est-à-dire comme fonction de deux variables indépendantes. Cette représentation est, selon certains points de vue, meilleure que la représentation explicite ; cependant, on peut rencontrer des problèmes quand il faut expliciter l'une des deux variables en fonction de l'autre : souvent, c'est très compliqué, quand ce n'est pas impossible.

Représentation paramétrée

La meilleure représentation est sans aucun doute la représentation paramétrée, du type :

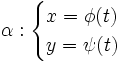$\alpha : \begin{cases} x = \phi(t) \\ y = \psi(t) \end{cases}$ ou bien

α(t) = (φ(t),ψ(t))

où $t \in I$ s'appelle le paramètre.

La condition de continuité ne suffit pas pour représenter et étudier les courbes vues comme objets filiformes à une dimension avec les caractéristiques de régularité voulues. La condition supplémentaire est que la courbe plane soit différentiable sur $I$ .

Une courbe plane paramétrée $α(t) = (φ(t),ψ(t))$ est dite différentiable en tout point si les fonctions $φ(t)$ et $ψ(t)$ ont des dérivées continues en tout point.

On dit qu'une courbe plane paramétrée est régulière en un point $t 0$ (ou que $t 0$ est un point régulier pour cette courbe) si $\alpha'(t_0) = (\phi'(t_0), \psi'(t_0)) \ne (0,0)$ ; elle est dite régulière sur I si $\forall t \in I , \alpha'(t) \ne (0,0)$ en tout point $t$ de $I$ .

Un point $t 0$ tel que $α'(t 0) = (0,0)$ est appelé point singulier pour la courbe.

Tangente

La régularité de la courbe permet de définir la droite tangente à la courbe. Soient $α(t)$ une courbe différentiable et $P 0 = α(t 0)$ un point régulier. On peut définir la tangente à la courbe en ce point comme étant la droite passant par $P 0$ et parallèle au vecteur $α'(t 0) = (φ'(t 0),ψ'(t 0))$ .

La tangente a une équation cartésienne au point $t 0$ :

$\psi'(t_0) \cdot (\phi(t_0) - \phi(t)) - \phi'(t_0) \cdot (\psi(t_0) - \psi(t)) = 0$

et pour équations paramétrées :

$\begin{cases} \phi(t) = \phi'(t_0) (t-t_0) + \phi(t_0) \\ \psi(t) = \psi'(t_0) (t-t_0) + \psi(t_0) \end{cases}$

Dans le cas d'une courbe représentée explicitement par une équation $y = f (x)$ , la tangente au point $(x 0, y 0)$ est donnée par la relation :

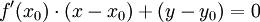$f'(x_0) \cdot (x-x_0) + (y-y_0) = 0$ .

Dans le cas d'une courbe représentée par une équation implicite $F (x, y) = 0$ , la tangente au point $(x 0, y 0)$ est donnée par la relation :

$F_{x_0}\cdot(x-x_0) + F_{y_0}\cdot(y-y_0) = 0$

où $F_{x_0}$ (respectivement $F_{y_0}$ ) désigne la dérivée partielle par rapport à $x$ (respectivement $y$ ) de $F$ , évaluée au point $x 0$ (respectivement $y 0$ ).

Normale

La régularité de la courbe permet de définir la droite normale à la courbe au point $t 0$ , d'équation cartésienne :

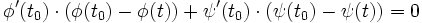$\phi'(t_0) \cdot (\phi(t_0) - \phi(t)) + \psi'(t_0) \cdot (\psi(t_0) - \psi(t)) = 0$ .

Cette équation devient, avec les mêmes notations que dans le paragraphe précédent :

Pour une représentation explicite :

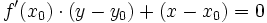$f'(x_0) \cdot (y-y_0) + (x-x_0) = 0$ .

Pour une représentation implicite :

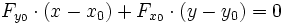$F_{y_0}\cdot(x-x_0) + F_{x_0}\cdot(y-y_0) = 0$ .

Cosinus directeurs

D'après la définition même de la dérivée, on obtient :

$\frac {\phi(t)}{\psi(t)} = \tan \theta$

ce qui, d'un point de vue géométrique, représente la pente de la droite tangente à la courbe, autrement dit la tangente (au sens trigonométrique du terme) de l'angle que cette tangente forme avec l'axe horizontal (l'axe des 'x'). De cette relation, on peut extraire les cosinus directeurs de la tangente à la courbe :

$\cos \theta = \pm \frac {\phi'(t)}{\sqrt{\phi'(t)^2 + \psi'(t)^2}}$

$\sin \theta = \pm \frac {\psi'(t)}{\sqrt{\phi'(t)^2 + \psi'(t)^2}}$

Reparamétrage

Soient $\alpha : I \longrightarrow \R^2$ une courbe plane différentiable, et $t = t (s)$ une fonction définie sur l'intervalle $S$ et à valeurs dans $I$ . Alors la courbe :

$\beta = \alpha \circ t : S \longrightarrow \R^2,$

telle que pour tout $s \in S, \beta(s) = \alpha(t(s))$ , est un reparamétrage de la courbe $α$ . Le reparamétrage est dit régulier si $t (S) = I$ et si $\forall s \in S, t'(s) \ne 0$ .

On vérifie alors le théorème suivant : si $\beta = \alpha \circ t$ est un reparamétrage de la courbe $α$ par $t = t (s)$ alors

$\beta' (s) = \frac {dt}{ds} \alpha' (t(s))$

Démonstration

α(t) = (φ(t),ψ(t))

alors

β(s) = (φ(t (s)),ψ(t (s)))

et d'après les théorèmes de dérivation des fonctions composées, on a :

$\frac {d\phi(t(s))}{ds} = \frac {d\phi}{dt} \cdot \frac {dt}{ds}$

$\frac {d\psi(t(s))}{ds} = \frac {d\psi}{dt} \cdot \frac {dt}{ds}$

et ainsi on obtient :

$\beta'(s) = \frac {dt}{ds} \left(\frac {d\phi}{dt} , \frac {d\psi}{dt} \right) = \frac {dt}{ds} \alpha'(t(s))$

Longueur d'une courbe

Longueur d'un arc paramétré

Soient $α(t) = (φ(t),ψ(t))$ une courbe différentiable sur I, et $[a,b]\subseteq I$ . Alors la longueur de l'arc de courbe compris entre $α(a)$ et $α(b)$ vaut :

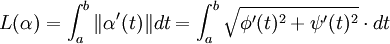$L(\alpha) = \int_{a}^{b} \| \alpha'(t) \| dt = \int_{a}^{b} \sqrt{\phi'(t)^2 + \psi'(t)^2} \cdot dt$ .

Si de plus $β(s)$ est un reparamétrage de la courbe, alors :

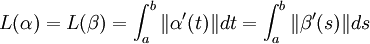$L(\alpha) = L(\beta) = \int_{a}^{b} \| \alpha'(t) \| dt = \int_{a}^{b} \| \beta'(s) \| ds$ .

Longueur et forme cartésienne explicite

Si la courbe est représentée sous forme cartésienne explicite $y = f (x)$ alors, comme $\frac{dx}{dx} = 1$ et $\frac {df(x)}{dx} = \frac {dy}{dx}$ , la longueur de la courbe est donnée par :

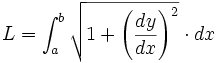$L = \int_{a}^{b}{\sqrt{1+\left(\frac{dy}{dx}\right)^2}\cdot dx}$ .

Paramétrage avec les coordonnées polaires planes

Une forme de paramétrage qui revêt une importance notable dans l'étude des mathématiques, de la géométrie et dans de nombreux domaines d'application des mathématiques, est celle des coordonnées polaires planes. Étant donnée une courbe paramétrée en coordonnées polaires par la forme cartésienne $r = r (θ)$ , avec c ≤ θ ≤ d, et par la forme paramétrée :

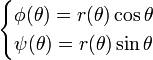$\begin{cases} \phi(\theta) = r(\theta) \cos \theta \\ \psi(\theta) = r(\theta) \sin \theta \end{cases}$ , de paramètre θ.

Alors ses dérivées sont : 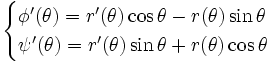$\begin{cases}\phi'(\theta) = r'(\theta) \cos \theta - r(\theta) \sin \theta \\ \psi'(\theta) = r'(\theta) \sin \theta + r(\theta) \cos \theta \end{cases}$

et donc la longueur de l'arc est :

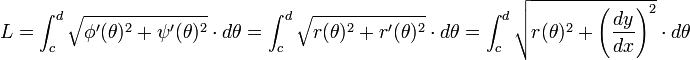$L = \int_{c}^{d}{\sqrt {\phi'(\theta)^2 + \psi'(\theta)^2} \cdot d\theta} = \int_{c}^{d}{\sqrt {r(\theta)^2 + r'(\theta)^2} \cdot d\theta} = \int_{c}^{d}{\sqrt {r(\theta)^2 + \left(\frac {dy}{dx} \right)^2} \cdot d\theta}$ .

Abscisse curviligne

On définit l'abscisse curviligne ou paramètre longueur d'arc comme étant le reparamétrage particulier obtenu en fixant la borne inférieure d'intégration a, de façon à ce que l'intégrale $s(t) = \int_{a}^{t}{\| \alpha'(u) \| du}$ ne dépende que de la borne supérieure t, vue comme variable. Cette fonction est, géométriquement, la longueur de l'arc de courbe à partir d'un point fixe a, affectée éventuellement d'un signe. Il est toujours possible de paramétrer de nouveau la courbe selon l'abscisse curviligne. Dans ce cas, pour déterminer la tangente en un point, on sait qu'elle est parallèle à un vecteur tangent unitaire. On démontre que l'on peut toujours paramétrer de nouveau une courbe au moyen de l'abscisse curviligne de la façon suivante :

étant donné que $s'(t) = \|\alpha'(t)\| width=$ 0" />, on peut inverser $s (t)$ , et son inverse est $t = t (s)$ . Alors on obtient le reparamétrage par l'abscisse curviligne donné par : $β(s) = α(t (s))$ .

On démontre ensuite que le vecteur tangent est unitaire :

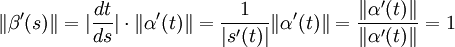$\| \beta'(s) \| = | \frac {dt}{ds} | \cdot \| \alpha'(t) \| = \frac {1}{|s'(t)|} \| \alpha'(t) \| = \frac {\| \alpha'(t) \|}{\| \alpha'(t) \|} = 1$ .

Courbure

Soit $β(s)$ une courbe paramétrée selon l'abscisse curviligne et $β'(s)$ son vecteur tangent unitaire. Considérons la fonction $k : S\longrightarrow \R , s\longmapsto k(s) = \| \beta'(s)\|$ . Alors la fonction $k(s) \ge 0$ est dite courbure de la courbe.

Si la courbe est représentée explicitement, sa courbure est :

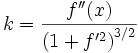$k = \frac{f''(x)}{ \left(1 + f'^{2} \right)^{3/2}}$ .

En revanche, pour une courbe représentée par une équation implicite, la courbure est évaluée par :

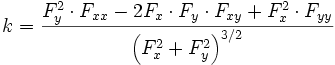$k = \frac{F_{y}^{2} \cdot F_{xx} - 2 F_{x} \cdot F_{y} \cdot F_{xy} + F_{x}^{2} \cdot F_{yy}}{\left(F_{x}^{2} + F_{y}^{2} \right)^{3/2}}$ .

Formules de Frenet

Une courbe (suffisamment régulière) de l'espace possède, en tous ses points, un système de référence, dit trièdre de Frenet, donné par un triplet de vecteurs tangent, normal e binormal. Une telle courbe est plane si et seulement si le vecteur binormal est toujours nul.

Soit $β(s) = (φ(s),ψ(s))$ une courbe paramétrée selon l'abscisse curviligne. Le vecteur unitaire tangent est déterminé par :

T (s) = β'(s) = (φ'(s),ψ'(s)).

Le vecteur unitaire normal est déterminé par :

$N(s) = i \cdot T(s) = (- \psi'(s), \phi'(s)),$

où i est le nombre complexe tel que $i 2 = - 1$ . Grâce à la définition de la courbure, on peut donner une autre forme au vecteur unitaire normal :

$N(s) = \frac {T'(s)}{\| T'(s) \|} = \frac {T'(s)}{k(s)}.$

On démontre que le vecteur $T'$ est orthogonal à T et donc parallèle à N.

Finalement, les formules di Frenet et la courbure pour une courbe plane, quel que soit son paramétrage $α(t) = (φ(t),ψ(t))$ , sont :

$T(t) = \frac {\alpha'(t)}{\| \alpha'(t) \|}$

$N(t) = \frac {i \cdot \alpha'(t)}{\| \alpha'(t) \|}$

$k(t) = \frac {\alpha''(t) \cdot (i \alpha'(t))}{\| \alpha'(t) \|^3}$

Exemples de courbes planes

Courbes planes classiques

La droite

Le cercle
- Le cercle unité

les cissoïdes :
- La cissoïde de Dioclès
- La cissoïde de Sluze

Les coniques :
- l'ellipse
- la parabole
- l'hyperbole

les courbes cycloïdales :
- la cycloïde
- l'épicycloïde
- l'hypocycloïde
- la cardioïde
- la néphroïde
- l'astroïde
- la deltoïde

Les courbes isochrones :
- L'isochrone de Huygens
- L'isochrone de Leibniz
- L'isochrone paracentrique
- L'isochrone de Varignon

les lemniscates :
- Le lemniscate de Bernoulli
- Le lemniscate de Gerono
- Le lemniscate de Booth

Les spirales :
- La spirale d'Archimède
- La spirale hyperbolique
- La spirale logarithmique
- La spirale de Fermat
- La spirale de Nielsen
- La spirale de Cotes
- La spirale de Galilée

la sinusoïde
l'exponentielle
l' atriphtaloïde
la chaînette
Le folium de Descartes
l' hélice
les conchoïdes
le limaçon de Pascal
La lituus
Les pétales de rose
La strophoïde
La superellipse
la tractrice
La trisectrice de Maclaurin
la courbe du chien

les courbes enveloppes
les courbes développantes

Constructions

La courbe du dragon
Le flocon de Koch
Les courbes de Bézier
Les splines

Courbes analytiques

Courbe fermée
Courbe rectifiable
Courbe de Jordan
Courbe de Peano
Courbe de Sierpinski

Courbes algébriques

Une courbe algébrique est une variété algébrique de dimension 1, généralement exprimée sous la forme d'un polynôme de degré divers. Des exemples incluent :

Les droites projectives
Les courbes quadriques, autre nom des coniques, de degré 2
Les courbes cubiques, de degré 3
- La cubique d'Agnesi
Les courbes quartiques, de degré 4
- La courbe de Klein
Les courbes quintiques, de degré 5
- La quintique de l'Hospital
Les courbes sextiques, de degré 6
Les courbes elliptiques
Les courbes hyperelliptiques
Les courbes modulaires
Les courbes de Fermat

Observer directement le Big Bang avec un télescope plus puissant que le James Webb ?

Il y a 2 heures

Découverte de 17 variants génétiques liés à la maladie d'Alzheimer

Il y a 2 heures

Un immense glacier du Groenland est littéralement en train de fondre sous nos yeux

Il y a 4 heures

Découverte: des bactéries anticholestérol dans notre intestin

Il y a 4 heures

Des dinosaures aux oiseaux: cette anomalie de l'ADN a trompé les scientifiques

Il y a 21 heures

De la vie cachée 800 mètres sous terre: comment est-ce possible ?

Il y a 21 heures

Analyse d'un signal radio inhabituel, en provenance de cet objet spatial extrême

Il y a 1 jour

Ce liquide est programmable, pouvant changer de consistance et de couleur

Il y a 1 jour

Un trou noir trop léger, ou une étoile à neutrons trop lourde ? L'objet qui intrigue les scientifiques

Il y a 1 jour

Un lien démontré entre vapotage, petit-déjeuner et maux de tête

Il y a 1 jour

Un immense "arc-en-ciel" détecté sur une exoplanète

Il y a 2 jours

Des scientifiques étudient 40 ans de vie marine dans... des conserves de saumon

Il y a 2 jours

Cette innovation va améliorer significativement la sensibilité des détecteurs d'ondes gravitationnelles

Il y a 2 jours

Découverte d'une ingénierie humaine vieille de... 300 000 ans

Il y a 2 jours

Psyche: une mission à la découverte de ce très mystérieux objet spatial

Il y a 3 jours

Peur généralisée: des scientifiques découvrent comment ne pas être tétanisé par la peur

Il y a 3 jours

Découverte accidentelle d'une mémoire quantique au potentiel énorme

Il y a 3 jours

Des chercheurs ont créé artificiellement des "minifoies"

Il y a 3 jours

Surprise: la surface lunaire a "coulé" sous la croûte

Il y a 3 jours

Un curieux "point de bascule" découvert dans l'évolution des champignons

Il y a 3 jours

Des humains préhistoriques ont gravé ces traces de dinosaures

Il y a 4 jours

Ralentissement significatif d'importants courants océaniques: des répercussions graves ?

Il y a 4 jours

Les étoiles à neutrons, des aspirateurs de matière noire ?

Il y a 4 jours

Greffer de la peau de porc pour soigner les plaies

Il y a 4 jours

Le secret d'une jeunesse éternelle à proximité du trou noir de notre Voie Lactée

Il y a 4 jours

Une quantité phénoménale de volcans cachés sous l'Antarctique: des risques d'éruption ?

Il y a 4 jours

Une mission spatiale dans l'espace interstellaire, à 1000 unités astronomiques ?

Il y a 5 jours

Ce régime montre une efficacité contre la maladie d'Alzheimer

Il y a 5 jours

Les dinosaures contredisent ce principe scientifique

Il y a 5 jours

Sentons-nous le goût des aliments uniquement avec notre langue ?

Il y a 5 jours

Nova: une rare et impressionnante explosion stellaire bientôt visible dans le ciel

Il y a 5 jours

Découverte d'une importante vertu anti-vieillissement à cette vitamine

Il y a 5 jours

Quand le cerveau ne perçoit que des visages distordus: la prosopométamorphopsie

Il y a 6 jours

La future station lunaire Gateway sous le feu des radiations spatiales

Il y a 6 jours

Cette découverte pourrait améliorer considérablement l'efficacité des traitements contre le cancer

Il y a 6 jours

Les orages violents en France sont déjà intensifiés par le changement climatique

Il y a 6 jours

La gravité quantique étudiée au Pôle Sud

Il y a 6 jours

Moins d'arbres, plus de mercure dans l'air: l'inquiétante étude du MIT

Il y a 6 jours

James Webb découvre les premières lumières de l'Univers

Il y a 7 jours

Une IA révèle un nouvel antibiotique, capable de détruire le staphylocoque doré multirésistant

Il y a 7 jours

Le cerveau dévoilé comme jamais grâce à l'IRM le plus puissant au monde

Il y a 7 jours

Existe-t-il des solutions au mal des transports ?

Il y a 7 jours

Efficacité des panneaux solaires: le pérovskite dépasse le silicium

Il y a 7 jours

Vie artificielle: une étape cruciale franchie

Il y a 7 jours

L'énergie sombre ne serait pas constante: vers un bouleversement de la cosmologie ?

Il y a 8 jours

Ce béton innovant fait fondre naturellement glace et neige: comment ?

Il y a 8 jours

Saveur, texture, préparation... la science du chocolat décortiquée

Il y a 8 jours

Cancers: une nouvelle piste pour améliorer l'efficacité des immunothérapies

Il y a 8 jours

La NASA réfléchit à un fuseau horaire lunaire, la cause à la relativité d'Einstein

Il y a 9 jours

Un nouveau mécanisme pour former des magnétars: la simulation

Il y a 9 jours

Populaires

De la vie cachée 800 mètres sous terre: comment est-ce possible ?

Observer directement le Big Bang avec un télescope plus puissant que le James Webb ?

Analyse d'un signal radio inhabituel, en provenance de cet objet spatial extrême

Des dinosaures aux oiseaux: cette anomalie de l'ADN a trompé les scientifiques

Découverte de 17 variants génétiques liés à la maladie d'Alzheimer

Un immense glacier du Groenland est littéralement en train de fondre sous nos yeux

Toutes les ventes flash et Codes Promos Amazon

Cdiscount: les meilleures réductions actuelles

Page générée en 2.310 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise