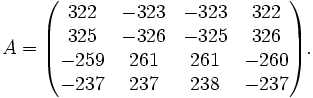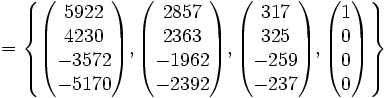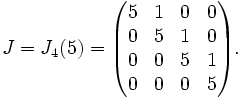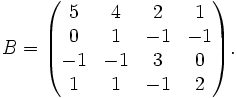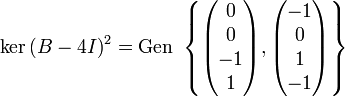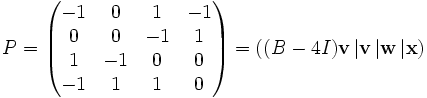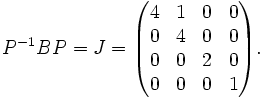Réduction de Jordan - Définition
La réduction de Jordan est la traduction matricielle de la réduction des endomorphismes introduite par Jordan. Cette réduction est tellement employée, en particulier en analyse pour la résolution d'équations différentielles ou pour déterminer le terme général de suites récurrentes, qu'on la nomme parfois " jordanisation des endomorphismes ".
Elle consiste à exprimer la matrice d'un endomorphisme dans une base réduite dite base de Jordan. La réduction consiste à déterminer une décomposition de Dunford c'est-à-dire trouver un endomorphisme diagonalisable et un endomorphisme nilpotent tel que les deux commutent et que leur somme soit égale à l'endomorphisme initial, puis sur chaque espace caractéristique une réduction de Jordan sur le facteur l'endomorphisme nilpotent.
Construction de la base de Jordan
Soit u un endomorphisme sur un espace vectoriel E tel que son polynôme minimal soit scindé. Il possède alors les propriétés suivantes:
-
- E est la somme directe des espaces caractéristiques de u. Ils sont notés ici Ei et les valeurs propres associés λi.
-
- La restriction de u à Ei est la somme d'une homothétie de rapport λi et d'un endomorphisme nilpotent noté ni.
Ces résultats sont démontrés dans l'article décomposition de Dunford.
-
- Il existe une base Eij de Ei
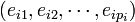 tel que
tel que 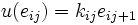 où
où 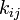 est égal soit à 0 soit à 1 et
est égal soit à 0 soit à 1 et 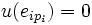 .
.
- Il existe une base Eij de Ei
Ce résultat est démontré dans l'article Endomorphisme nilpotent.
Blocs de Jordan
On appelle bloc de Jordan une matrice de la forme 
On appelle bloc de Jordan nilpotent une telle matrice où les coefficients diagonaux sont tous nuls, c'est-à-dire de la forme 
Jordanisation d'un endomorphisme dans un corps algébriquement clos
On considère un endomorphisme dans un espace vectoriel de dimension finie, de polynôme caractéristique scindé. Le théorème de Jordan nous informe qu'il admet une représentation matricielle de la forme suivante
où les scalaires λi sont les valeurs propres de l'endomorphisme considéré.
Ainsi sur un corps algébriquement clos, et par exemple dans ![]() , tout endomorphisme admet une décomposition de ce type.
, tout endomorphisme admet une décomposition de ce type.
Attention : il n'y a pas a priori un bloc de Jordan pour chaque valeur propre, plusieurs λi peuvent avoir la même valeur.
Propriétés des blocs
Prenons un endomorphisme u admettant une telle représentation. On étudie une valeur propre particulière λ de l'endomorphisme u. On regroupe ensemble les vecteurs associés aux blocs ![]() . Ils forment l'espace caractéristique associé à la valeur propre λ. C'est un espace stable sur lequel u − λId induit un endomorphisme nilpotent nλ.
. Ils forment l'espace caractéristique associé à la valeur propre λ. C'est un espace stable sur lequel u − λId induit un endomorphisme nilpotent nλ.
- La multiplicité de λ (multiplicité dans le polynôme caractéristique) est égale à la dimension de l'espace caractéristique.
- La multiplicité de λ dans le polynôme minimal est égal à l'indice de nilpotence de l'endomorphisme nλ.
Application aux classes de similitude des matrices
On se place sur un corps algébriquement clos. Deux matrices sont semblables si et seulement si elles ont la même écriture en blocs de Jordan, à l'ordre près des blocs.
Exemples de réduction de Jordan
Examinons les méthodes de détermination des matrices de passage par deux exemples.
Exemple 1
Déterminons la matrice de passage pour l'exemple suivant:
Recherchons les espaces caractéristiques, c’est-à-dire vecteurs x solutions de
Qui nous permettront de déterminer la suite de vecteurs dont les éléments forment les colonnes de la matrice de passage.
Remarquons alors que 5 est valeur propre et que le premier vecteur de la base de définition de la matrice possède pour polynôme minimal associé (X-5)4. Son espace caractéristique est donc l'espace entier. Si nous notons v ce vecteur alors, la famille composée des éléments (A − 5I)3(v), (A − 5I)2(v), (A − 5I)(v) et v forme une base de Jordan.
Nous avons déterminé la matrice de passage:
Et la matrice de Jordan est la suivante:
Exemple 2
Considérons l'exemple suivant
Les valeurs propres de B sont 4, 4, 2 et 1. De plus, on remarque que:
Nous en déduisons que l'espace vectoriel se décompose en somme directe suivante:
Nous remarquons que le vecteur colonne (0,0,−1,1)T a pour image par la matrice (-1,0,1,-1)T. Ces deux vecteurs colonnes engendrent l'espace caractéristique de valeur propre 4.
On en déduit
Nous en déduisons la matrice de passage et la forme de Jordan:
et
Réduction de Jordan et systèmes différentiels
Un système d'équations différentielles linéaires en y peut se réduire à une équation différentielle matricielle d'ordre 1 : u'(t) = Au(t) et la condition initiale u(0) = u0, où u(t) est un vecteur colonne contenant les dériviées successives de y. La résolution est alors explicite : u(t) = exp(tA)u0. L'avantage de la forme normale de Jordan réside dans la facilité de calculs des matrices des blocs de Jordan. En effet, l'exponentielle d'un bloc de Jordan nilpotent de taille p est 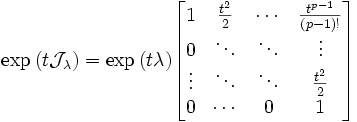
On voit de cette manière l'intérêt calculatoire de cette méthode.
| Articles de mathématiques en rapport avec l'algèbre linéaire |
| Espace vectoriel | Base | Dimension | Matrice | Application linéaire | Déterminant | Trace | Rang | Théorème des facteurs invariants | Réduction d'endomorphisme | Réduction de Jordan | Décomposition de Dunford | Valeur propre | Polynôme caractéristique | Forme linéaire | Espace dual | Orthogonalité | Produit scalaire | Produit vectoriel | Polynôme d'endomorphisme | Polynôme minimal | Tenseur | Pseudovecteur | Covecteur | Algèbre multilinéaire |