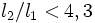Pendule double - Définition
Présentation
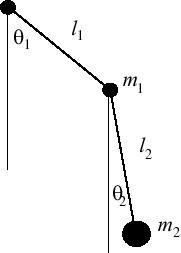
Exercice classique de mécanique, il s'agit d'un pendule à l'extrémité duquel on accroche un autre pendule. On a donc deux tiges de longueur
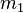
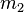
Mise en équation utilisant l'approche lagrangienne
L'énergie cinétique vaut :
![T=\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2=\frac{1}{2}m_1l_1^2\dot{\theta}_1^2 + \frac{1}{2}m_2[l_1^2\dot{\theta}_1^2+l_2^2\dot{\theta}_2^2 + 2l_1l_2\dot{\theta}_1\dot{\theta}_2\cos(\theta_1-\theta_2)]](https://static.techno-science.net/illustration/Definitions/autres/4/43b0e769893f994cb613be44d65e0412_25ec3455e4832deb57a7d5e46c2f48ec.png)
où
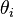
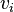
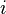
L'énergie potentielle vaut :
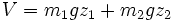
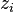
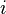
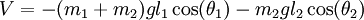
Le lagrangien vaut donc :
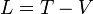
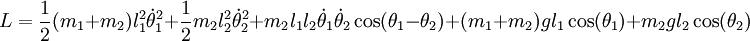
En appliquant les équations de Lagrange, on obtient les équations du mouvement :
(1)
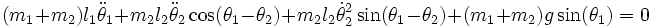
(2)
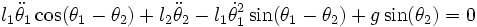
Ce système possède des solutions périodiques décomposables en deux modes, mais il est chaotique, c’est-à-dire qu'il possède aussi des solutions ni périodiques ni pseudo-périodiques, mais présentant en permanence un mouvement original, et qu'il est alors sensible aux conditions initiales.
Voir sur cette page une superbe simulation du pendule double.
Mise en équation utilisant l'approche newtonnienne
L'affixe de l'extrémité du premier pendule est
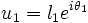
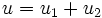
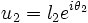
L'accélération de cette dernière vaut donc
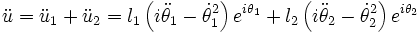
La relation fondamentale de la dynamique en
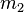
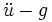
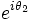
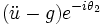
La relation fondamentale de la dynamique en
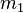
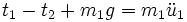
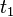
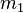
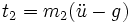
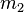
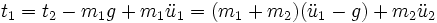
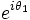
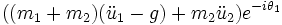
Pendule à entraînement circulaire uniforme
Une autre exercice classique concerne le cas où la première tige se meut d'un mouvement uniforme autour de son axe. On a alors
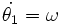
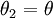
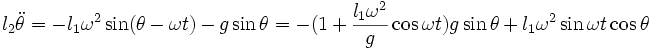
Pour de petites oscillations et
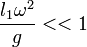
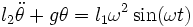
Mais si dans ce cas on choisit
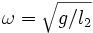
|
|
On constate que le pendule fait le tour si
|