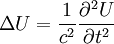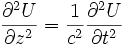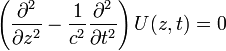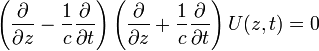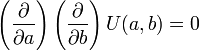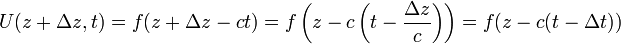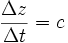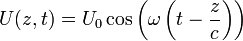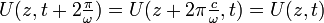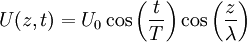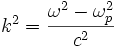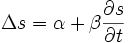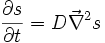🔎 Propagation des ondes : définition et explications

Propagation des ondes

champ électromagnétique diffusivité thermique onde stationnaire

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

La propagation des ondes est un domaine de la physique s'intéressant aux déplacements des ondes électromagnétiques dans les milieux. On distingue généralement deux catégories de propagation :

La propagation dans l'espace libre (vide, air (L'air est le mélange de gaz constituant l'atmosphère de la Terre. Il est inodore et incolore. Du fait de la diminution de la pression de l'air avec l'altitude, il est nécessaire de pressuriser les...), milieu massif (Le mot massif peut être employé comme :) comme le verre (Le verre, dans le langage courant, désigne un matériau ou un alliage dur, fragile (cassant) et transparent au rayonnement visible. Le plus souvent, le verre est constitué...), etc.)
La propagation guidée (fibre optique (L'optique est la branche de la physique qui traite de la lumière, du rayonnement électromagnétique et de ses relations avec la vision.), guide d'onde (Une onde est la propagation d'une perturbation produisant sur son passage une variation réversible de propriétés physiques locales. Elle transporte de l'énergie sans transporter...), etc.)

Équation (En mathématiques, une équation est une égalité qui lie différentes quantités, généralement pour poser le problème de leur identité. Résoudre l'équation consiste à déterminer toutes les façons de donner à certaines des...) d'onde (Une onde est la propagation d'une perturbation produisant sur son passage une variation réversible des propriétés physiques locales. Elle transporte de l'énergie sans transporter de matière. Une onde...)

L'équation générale qui décrit la propagation d'une onde $\vec E$ dans l'espace libre, dans un milieu homogène, linéaire et isotrope est :

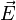
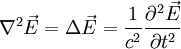
$\nabla^2 \vec E=\Delta\vec E=\frac {1}{c^2}\frac {\partial ^2\vec E}{\partial t^2}$ (établissement de l'équation de propagation à partir des équations de Maxwell)

$\vec E$ décrit à la fois l'amplitude (Dans cette simple équation d’onde :) de l'onde, et sa polarisation ( la polarisation des ondes électromagnétiques ; la polarisation dûe aux moments dipolaires dans les matériaux diélectriques ; En...) (par son caractère vectoriel). C'est assimilable à la vitesse (On distingue :) de propagation de l'onde, comme nous le verrons plus bas.

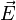
Si l'on s'intéresse à ce qui se passe pour chacune des composantes de $\vec E$ (en projetant la relation dans chacune des directions de l'espace), nous obtenons une équation portant sur un scalaire (Un vrai scalaire est un nombre qui est indépendant du choix de la base choisie pour exprimer les vecteurs, par opposition à un pseudoscalaire, qui est un...), appelée équation de d'Alembert :

$\Delta U=\frac {1}{c^2}\frac {\partial ^2 U}{\partial t^2}$

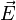
Intéressons nous à la propagation selon la seule direction $z$ :

$\frac {\partial ^2 U}{\partial z^2}=\frac {1}{c^2}\frac {\partial ^2 U}{\partial t^2}$

Pour une onde plane (L'onde plane est un concept issu de la physique de la propagation des ondes. C'est une onde dont les fronts d'onde sont des plans infinis, tous...), la solution générale de cette équation est la somme de deux fonctions :

U (z, t) = f (z - c t) + g (z + c t)

En effet, on peut écrire :

$\left(\frac {\partial ^2}{\partial z^2}-\frac {1}{c^2}\frac {\partial ^2}{\partial t^2}\right) U(z,t) = 0$

soit :

$\left(\frac {\partial}{\partial z}-\frac {1}{c}\frac {\partial}{\partial t}\right)\left(\frac {\partial}{\partial z}+\frac {1}{c}\frac {\partial}{\partial t}\right) U(z,t) = 0$

Et si l'on pose a=z-ct et b=z+ct, on obtient :

$\left(\frac {\partial}{\partial a}\right)\left(\frac {\partial}{\partial b}\right) U(a,b) = 0$

Qui se résout en : $U (a, b) = f (a) + g (b)$ soit $U (z, t) = f (z - c t) + g (z + c t)$

Le premier terme est une onde se propageant dans le sens (SENS (Strategies for Engineered Negligible Senescence) est un projet scientifique qui a pour but l'extension radicale de l'espérance de vie humaine. Par une évolution progressive allant du ralentissement du vieillissement,...) des z croissants (appelée onde progressive), et le deuxième terme dans le sens des z décroissants (appelée onde régressive).

Vitesse de propagation

Il est intéressant de voir qu'en réalité, l'onde $U (z, t)$ ne dépend pas simplement de $z$ et de $t$ , mais des quantités $z - c t$ et $z + c t$ . Pour comprendre ce que cela signifie, considérons le cas d'une onde plane (La plane est un outil pour le travail du bois. Elle est composée d'une lame semblable à celle d'un couteau, munie de deux poignées, à chaque extrémité de la lame. Elle permet le...) progressive vers les z croissants :

U (z, t) = f (z - c t)

Regardons la structure de l'onde au point (Graphie) $z + Δ z$ :

$U(z+\Delta z,t)=f(z+\Delta z-ct)=f\left(z-c\left(t-\frac {\Delta z}{c}\right)\right)=f(z-c(t-\Delta t))$

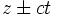
L'expression ci-dessus nous montre que la structure de l'onde au point $z + Δ z$ est la même qu'au point $z$ à l'instant (L'instant désigne le plus petit élément constitutif du temps. L'instant n'est pas intervalle de temps. Il ne peut donc être considéré comme une durée.) $t - Δ t$ , avec $Δ t = Δ z / c$ . Ce raisonnement nous permet de comprendre pourquoi une dépendance en $z \pm ct$ de l'onde signifie que celle-ci se déplace sans déformation, i.e qu'il s'agit d'une onde progressive.

Nous pouvons alors définir la vitesse de propagation de l'onde par :

$\frac {\Delta z}{\Delta t}=c$

Onde harmonique (Dans plusieurs domaines, une harmonique est un élément constitutif d'un phénomène périodique ou vibratoire (par exemple en électricité : les « courants harmoniques », qui sont des perturbations du...) - période et fréquence (En physique, la fréquence désigne en général la mesure du nombre de fois qu'un phénomène périodique se reproduit par unité de temps. Ainsi lorsqu'on...)

Une onde harmonique est une onde monochromatique (On qualifie de monochromatique (du grec mono-, un seul et chromos, couleur) une lumière dont la couleur n'est formée que d'une fréquence ou, par extension de sens, d'une bande très étroite de...) dont l'expression est donnée (Dans les technologies de l'information, une donnée est une description élémentaire, souvent codée, d'une chose, d'une transaction, d'un événement, etc.) dans notre cas par :

$U(z,t) = U_0\cos\left(\omega\left(t-\frac{z}{c}\right)\right)$

La propriété essentielle de cette onde est sa double périodicité, spatiale et temporelle :

$U(z, t+2\tfrac\pi\omega) = U(z+2\pi \tfrac c\omega,t)=U(z,t)$

On définit alors les quantités suivantes :

La fréquence de l'onde $ν = ω / 2π$ ( $ω$ est appelé pulsation)
La longueur (La longueur d’un objet est la distance entre ses deux extrémités les plus éloignées. Lorsque l’objet est filiforme ou en forme de lacet, sa longueur est celle de...) d'onde $λ = c / ν$
Le nombre (La notion de nombre en linguistique est traitée à l’article « Nombre grammatical ».) d'onde $k = 2π / λ$

À trois dimensions, le nombre d'onde est remplacé par le vecteur (En mathématiques, un vecteur est un élément d'un espace vectoriel, ce qui permet d'effectuer des opérations d'addition et de multiplication par un scalaire. Un n-uplet peut constituer un exemple de...) d'onde, dont le sens est celui de la propagation de l'onde.

Ondes progressives et ondes stationnaires

Onde progressive

Il est d'usage (L’usage est l'action de se servir de quelque chose.) dans la communauté scientifique (Un scientifique est une personne qui se consacre à l'étude d'une science ou des sciences et qui se consacre à l'étude d'un domaine avec la rigueur et les méthodes scientifiques.) de distinguer les ondes progressives des ondes stationnaires. Les ondes progressives, décrites précédemment, avancent dans l'espace.

Les ondes stationnaires, au contraire, oscillent sans se déplacer. Ainsi, elles ne dépendent plus du seul paramètre (Un paramètre est au sens large un élément d'information à prendre en compte pour prendre une décision ou pour effectuer un calcul.) $z - c t$ , mais des paramètres d'espace $z$ et de temps (Le temps est un concept développé par l'être humain pour appréhender le changement dans le monde.) $t$ de façon indépendante. Une expression simple d'une onde stationnaire (Une onde stationnaire est le phénomène résultant de la propagation simultanée dans des directions différentes de plusieurs ondes de même fréquence, dans le même milieu...) harmonique à une dimension (Dans le sens commun, la notion de dimension renvoie à la taille ; les dimensions d'une pièce sont sa longueur, sa largeur et sa profondeur/son épaisseur, ou bien son diamètre si c'est une...) est la suivante :

$U(z,t)=U_0\cos\left(\frac {t}{T}\right)\cos\left(\frac {z}{\lambda}\right)$

Onde stationnaire

À un temps $t$ fixé, une onde stationnaire ressemble à une onde progressive. En revanche, son évolution temporelle est totalement différente (En mathématiques, la différente est définie en théorie algébrique des nombres pour mesurer l'éventuel défaut de dualité d'une application définie à l'aide de la trace, dans...). Une onde stationnaire possède des minima (nœuds) et des maxima (ventres) d'amplitude fixes dans l'espace. Ainsi, si on se place aux nœuds de cette onde, l'amplitude est nulle quel que soit le temps. Avec une onde progressive, nous aurions vu l'amplitude évoluer, de façon sinusoïdale avec la temps dans le cas d'une onde harmonique.

Une façon simple de construire une onde stationnaire est de superposer deux ondes progressives se propageant en sens inverse (En mathématiques, l'inverse d'un élément x d'un ensemble muni d'une loi de composition interne · notée multiplicativement, est un élément y tel que x·y = y·x =...). C'est d'ailleurs ce qui se passe lorsque une onde se réfléchit sur un miroir (Un miroir est un objet possédant une surface suffisamment polie pour qu'une image s'y forme par réflexion et conçu à cet effet. C'est souvent une couche métallique fine, qui, pour être protégée, est...) parfait.

Les ondes stationnaires sont des objets physiques très courants et se rencontrent notamment dans les cavités laser (Un laser est un appareil émettant de la lumière (rayonnement électromagnétique) amplifiée par émission stimulée. Le terme laser provient de l'acronyme...) ou les lignes hyperfréquence.

Phénomènes affectant la propagation des ondes (La propagation des ondes est un domaine de la physique s'intéressant aux déplacements des ondes électromagnétiques dans les milieux. On distingue généralement deux catégories...)

Réflexion
Réfraction (En physique des ondes — notamment en optique, acoustique et sismologie — le phénomène de réfraction est la déviation d'une onde...)
Diffusion (Dans le langage courant, le terme diffusion fait référence à une notion de « distribution », de « mise à disposition » (diffusion d'un produit, d'une...)
Interférences
Diffraction (La diffraction est le comportement des ondes lorsqu'elles rencontrent un obstacle qui ne leur est pas complètement transparent ; le phénomène peut être...)

Plusieurs équations d'onde

Equation d'onde classique

L'équation d'onde classique correspond à une propagation non perturbée. Par exemple, corde vibrante sans frottement (Les frottements sont des interactions qui s'opposent à la persistance d'un mouvement relatif entre deux systèmes en contact.), onde électromagnétique dans le vide (Le vide est ordinairement défini comme l'absence de matière dans une zone spatiale.). Elle s'écrit $Δ s = 0$

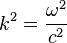
La relation de dispersion (La dispersion, en mécanique ondulatoire, est le phénomène affectant une onde dans un milieu dispersif, c'est-à-dire dans lequel les différentes fréquences...) associée est $k^2 = \frac{\omega^2}{c^2}$

Équation de Klein-Gordon

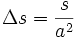
C'est une équation du type $\Delta s = \frac{s}{a^2}$ .

On la rencontre en particulier pour la propagation d'une onde électromagnétique dans un plasma ( En physique, le plasma décrit un état de la matière constitué de particules chargées (d'ions et d'électrons). Le plasma quark-gluon est un plasma qui constituerait...).

Soit $n$ la densité (La densité ou densité relative d'un corps est le rapport de sa masse volumique à la masse volumique d'un corps pris comme référence. Le corps de référence est...) particulaire du plasma et $m$ la masse (Le terme masse est utilisé pour désigner deux grandeurs attachées à un corps : l'une quantifie l'inertie du corps (la masse inerte) et l'autre la contribution du corps à la...) de l'électron (L'électron est une particule élémentaire de la famille des leptons, et possèdant une charge électrique élémentaire de signe négatif. C'est un des composants de l'atome.). On introduit la pulsation plasma

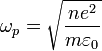
$\omega_p = \sqrt{\frac{ne^2}{m \varepsilon_0}}$ ,

grandeur caractéristique du plasma.

L'équation de propagation du champ (Un champ correspond à une notion d'espace défini:) $\vec E$ dans ce plasma est

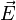
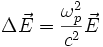
$\Delta \vec E = \frac{\omega_p^2}{c^2} \vec E$ .

La relation de dispersion associée est

$k^2 = \frac{\omega^2 - \omega_p^2}{c^2}$

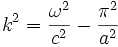
Remarque : on peut également rencontrer cette équation de dispersion dans le cadre de la propagation guidée. Par exemple, une onde guidée entre deux plans infinis et parfaitement conducteurs distants de $a$ vérifie l'équation d'onde classique entre les deux conducteurs, mais la relation de dispersion s'écrit $k^2 = \frac{\omega^2}{c^2} - \frac{\pi^2}{a^2}$

On rencontre également cette équation pour la propagation d'une onde mécanique : par exemple pour une série de pendules régulièrement espacés et reliés entre eux par des ressorts.

Equation des télégraphistes

Equation du type

$\Delta s = \alpha + \beta \frac{\partial s}{\partial t}$

On la rencontre dans le cas d'une onde dans une ligne électrique. Pour une ligne électrique de résistance linéique $r$ , d'inductance (L'inductance d’un circuit électrique est un coefficient qui traduit le fait qu’un courant le traversant crée un champ magnétique à travers la section entourée par ce circuit. Il en résulte un flux du champ magnétique...) linéique $c$ , de conductance de fuite linéique $g$ et de capacité linéique $c$ , on a :

$\frac{\partial^2 u}{\partial x^2} - lc \frac{\partial^2 u}{\partial t^2} = (rc+lg) \frac{\partial u}{\partial t} + rg \cdot u$

Cela traduit une propagation avec atténuation (Perte d'intensité et amplitude d'un signal...).

Relation de dispersion associée : $k 2 = l c ω 2 + i ω(r c + l g) - r g$

Equation de diffusion

Equation du type

$\frac{\partial s}{\partial t} = D \vec \nabla^2 s$

Le coefficient (En mathématiques un coefficient est un facteur multiplicatif qui dépend d'un certain objet, comme une variable (par exemple, les coefficients d'un polynôme), un espace...) $D$ est appelé coefficient de diffusivité.

On le rencontre typiquement dans deux cas :

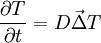
L'équation de la chaleur (Dans le langage courant, les mots chaleur et température ont souvent un sens équivalent : Quelle chaleur !) $\frac{\partial T}{\partial t} = D \vec \Delta T$ , où le coefficient de diffusivité thermique (La diffusivité thermique est la vitesse de pénétration et atténuation d'une onde thermique dans un milieu. 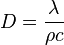La diffusivité thermique est souvent désignée par la...) $D$ est défini par $D = \frac{\lambda}{\rho c}$
Propagation d'un champ électromagnétique (Le champ électromagnétique est le concept central de l'électromagnétisme. On le conçoit souvent comme composition des deux champs vectoriels que...) dans un métal (Un métal est un élément chimique qui peut perdre des électrons pour former des cations et former des liaisons métalliques ainsi que des liaisons ioniques...) de conductivité $γ$ . Equation d'onde :
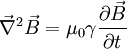
$\vec \nabla^2 \vec B = \mu_0 \gamma \frac{\partial \vec B}{\partial t}$ .
Relation de dispersion : $k 2 = - i ωμ 0 γ$ . Il s'agit d'une propagation avec atténuation.

Voir aussi

LHC: plus d'énergie pour les aimants du Synchrotron à protons

Un nouveau tamis moléculaire en oxyde de tungstène à coloration ajustable

Record de performance pour un capteur inertiel à atomes froids

Faire entrer la production de masse du graphène dans une nouvelle ère

Page générée en 0.126 seconde(s) - site hébergé chez Amen
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
Ce site est édité par Techno-Science.net - A propos - Informations légales
Partenaire: HD-Numérique