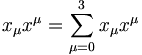Tenseur de Ricci - Définition
| Articles scientifiques sur les tenseurs |
| Mathématiques |
|
Produit tensoriel |
| Physique |
|
Convention d'Einstein |
| Articles connexes |
|
Modules |
| Portail des Mathématiques |
| Portail de la Physique |
Dans le cadre de la théorie de la Relativité générale, le champ de gravitation est interprété comme une déformation de l'espace-temps. Cette déformation est exprimée à l'aide du tenseur de Ricci, dont le nom a été attribué d'après son inventeur, Gregorio Ricci-Curbastro.
Le tenseur de Ricci est un tenseur d'ordre 2, obtenu comme la trace du tenseur de courbure complet. On peut le considérer comme le Laplacien du tenseur métrique riemannien dans le cas des variétés riemaniennes.
Le tenseur de Ricci occupe une place importante notamment dans l'équation d'Einstein, équation principale de la relativité générale. C'est aussi un objet fondamental en géométrie différentielle, le domaine de la géométrie qui essaye de décrire les propriétés géométriques des objets de dimension n.
Construction mathématique
Le tenseur de Ricci s'obtient à partir du tenseur de courbure de Riemann R, qui exprime la courbure de la variété (dans le cas de la Relativité générale, de l'espace-temps), à l'aide d'une réduction d'indices du tenseur.
Il peut s'exprimer notamment à partir des coefficients de Christoffel, qui représentent l'évolution des vecteurs de base d'un point à l'autre de l'espace-temps, due à la courbure de ce dernier. Ces coefficients dépendent alors directement de la métrique de l'espace (de la variété), qui est un outil mathématique permettant de définir les distances au sein de l'espace.
D'un point de vue mathématique, on parvient aux résultats suivant, en utilisant la convention de sommation d'Einstein[1].
Les coefficients de Christoffel s'expriment par :
Ces coefficients sont notamment utilisés pour écrire l'équation d'une géodésique, c'est-à-dire le chemin le plus court entre deux points de l'espace courbe - qui n'est pas toujours une ligne droite :
Le tenseur de courbure s'exprime à partir de ces mêmes coefficients de Christoffel :
Nous obtenons enfin le tenseur de Ricci par réduction :
Par la suite, la courbure scalaire se déduit à l'aide d'une nouvelle réduction :
La divergence du tenseur d'Einstein
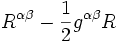
Cette équation fondamentale se démontre en mettant en jeu la nullité de la dérivée covariante du tenseur métrique.
C'est en identifiant le tenseur d'Einstein et le tenseur d'énergie-impulsion que l'on obtient l'équation d'Einstein qui fonde la relativité générale.
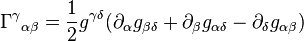
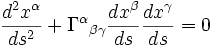
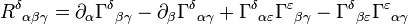
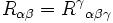
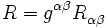
![\left[R^{\alpha\beta} - \frac{1}{2} g^{\alpha\beta} R\right]_{\alpha\beta} = 0](https://static.techno-science.net/illustration/Definitions/autres/4/4fb75eb84d5075195820bef8162ed4b5_bec7a6dfd5e59edd0e6682bbc6d4f812.png)