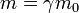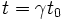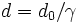Facteur de Lorentz - Définition

|
| Cet article de physique fait partie de la série relativité |
| Bases |
| histoire - théorie |
| Lorentz - Einstein - Mach |
| transformation de Lorentz |
| Feynman - Poincaré - Michelson |
| espace-temps-c - E=mc² - t |
| EQR |
| exp:Michelson et Morley |
| exp:pensée?-éther |
| jumeaux-train |
| relativité restreinte-générale |
| théorie de la relativité |
| controverse historique |
| Techniques |
| cyclotron |
| accélérateur de particules |
| Méta |
| article |
| Liens physique |
| Formulaire |
Le facteur de Lorentz est une grandeur physique intervenant dans de nombreuses formules de la relativité restreinte d'Einstein.
Il vaut
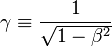
Quelques valeurs
La table suivante donne quelques valeurs du facteur de Lorentz correspondant à différentes valeurs de la vitesse, données en pourcentage de c.
| %c | γ | 1/γ |
|---|---|---|
| 0 | 1.000 | 1.000 |
| 10 | 1.005 | 0.995 |
| 50 | 1.155 | 0.867 |
| 90 | 2.294 | 0.436 |
| 99 | 7.089 | 0.141 |
| 99.9 | 22.366 | 0.045 |
Lorsque γ devient très grand devant 1 :
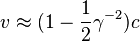
Principale utilisation
Le facteur de Lorentz s'applique à la dilatation temporelle, la contraction spatiale et à la masse relativiste dans la relativité restreinte.
En effet, considérons un corps de masse m0, un temps t0 et une distance d0 au repos. Plaçons-nous dans un référentiel se déplaçant à la vitesse v par rapport au référentiel d'origine. La masse, le temps et la distance apparents seront :
Démonstration
Tout d'abord, il faut rappeler que pour tout observateur, la lumière se déplace à une vitesse constante, très exactement :
- c = 299 792 458 m.s-1.
Imaginez deux observateurs :
Le premier observateur, A, voyage à la vitesse v avec un laser par rapport au second observateur B.
A pointe son laser vers le haut, perpendiculairement à la direction de son trajet. Du point de vue de B, le trajet de la lumière forme un angle. Après une période de temps t, A a parcouru, du point de vue de B, une distance d = vt; la lumière a parcouru une distance d = ct en formant un angle (cf. figure).
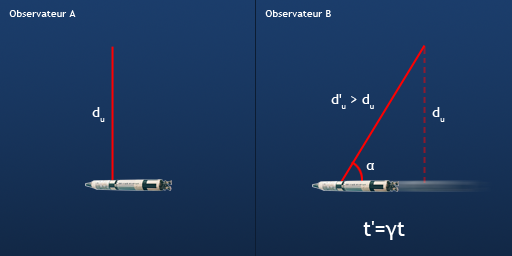
La composante verticale du trajet dt de la lumière peut être résolue par le théorème de Pythagore :
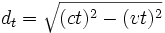
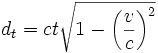
Cette distance est identique à celle que voit A. Puisque la lumière doit voyager à c, le temps de A, t', devra être égal à du/c. Donc :
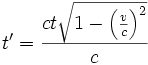
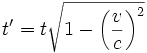
Autres propriétés
- En posant tanh(r) = β, alors γ = cosh(r). Ici, r est appelé rapidité. La rapidité possède la propriété d'être additive, ce que n'est pas la vélocité.
- Parfois, γ est écrit Γ plutôt que γ, quand on considère des vitesses hypothétiquement plus rapides que c.
- De nombreuses formules de la mécanique classique sont aisément transposables en mécanique relativiste grâce au facteur de Lorentz. En effet, il suffit de remplacer la masse du corps m par γm.