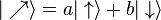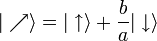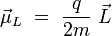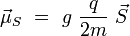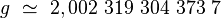Spin - Définition
Le spin est une propriété quantique intrinsèque associée à chaque particule, qui est caractéristique de la nature de la particule, au même titre que sa masse et sa charge électrique. Elle permet de caractériser le comportement de la particule sous l'effet de la symétrie de rotation de l'espace.
Définition simplifiée
La notion de spin permet de classer mathématiquement la façon dont se transforment les objets sous l'effet des rotations de l'espace à trois dimensions. De façon générale, un objet possède un spin

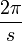
- Un objet sans symétrie particulière, par exemple une carte à jouer représentant un trois de trèfle, possède un spin 1 car il est nécessaire d'effectuer une rotation de
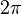
- Un objet possédant un peu plus de symétrie, comme une dame de pique par exemple, possède un spin 2 car pour qu'elle revienne à sa position de départ, on peut se contenter de lui faire effectuer une rotation de
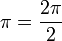
- Une étoile à cinq branches possède un spin 5 car il est suffisant de lui faire faire une rotation de
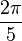
- Un objet complètement symétrique, comme une sphère par exemple, est invariante par rotation de n'importe quel angle. La définition simplifiée qu'on a donnée est difficile à appliquer dans ce cas mais mathématiquement il est naturel de dire qu'un tel objet possède un spin infini.
Remarquons que d'ordinaire, puisqu'une rotation d'angle
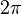
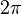
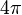

De façon plus rigoureuse, comme on va le voir plus bas, l'analyse du comportement des objets sous l'effet des rotations nécessite de prendre en compte la structure mathématique de groupe formé par celles-ci. À un objet se transformant sous les rotations est alors associée une représentation de groupe. Deux objets ayant des propriétés de symétrie similaires seront donc associés à des représentations équivalentes du groupe des rotations. De ce point de vue, le spin n'est rien d'autre qu'un nombre qui permet de classifier les différentes représentations inéquivalentes du groupe des rotations (on appelle cela les représentations irréductibles). C'est ainsi que l'on peut dire qu'une particule de spin 2 telle que le graviton (voir ci-dessous) possède la même symétrie du point de vue des rotations qu'une dame de pique car tous deux se transforment dans des représentations équivalentes.
Spin des particules usuelles
Le spin d'une particule est un nombre entier ou demi-entier positif, noté

Bien que lié aux phénomènes de quantification du moment angulaire, le spin est bel et bien une propriété intrinsèque des particules. En particulier, il ne correspond à aucun mouvement de rotation hypothétique de ces particules.
Les particules possédant un spin demi-entier s'appellent fermions, celles possédant un spin entier s'appellent bosons. Plus spécifiquement :
- Spin 0 : le boson de Higgs, particule hypothétique, non encore découverte expérimentalement.
- Spin 1/2 : l'électron, le positron, le proton, le neutron, les neutrinos, les quarks, etc.
- Spin 1 : le photon, les bosons W± et Z0 vecteurs de l'interaction faible.
- Spin 2 : le graviton, particule hypothétique vecteur de la gravitation.
Le spin de particules composées, comme le proton, le neutron, le noyau atomique ou l'atome, est constitué des spins des particules qui les composent auxquels s'ajoute le moment angulaire des particules élémentaires l'une par rapport à l'autre.
Historique
La notion de spin a été introduite par Pauli en décembre 1924 [PA25] pour l'électron afin d'expliquer un résultat expérimental qui restait incompréhensible dans le cadre naissant de la mécanique quantique non relativiste : l'effet Zeeman anormal. L'approche développée par Pauli consistait à introduire de façon ad-hoc le spin en ajoutant un postulat supplémentaire aux autres postulats de la mécanique quantique non relativiste (équation de Schrödinger, etc.).
L'introduction du spin permet de comprendre également d'autres effets expérimentaux, comme les doublets des spectres des métaux alcalins, ou le résultat de l'expérience de Stern et Gerlach.
En 1928, Paul Dirac construisit une version quantique et relativiste de l'équation de Schrödinger, appelée aujourd'hui équation de Dirac, qui permet de décrire les fermions de spin 1/2. Le spin y apparaît comme une propriété dérivée de son équation, et non comme un postulat supplémentaire à rajouter de façon ad-hoc.
Enfin, c'est en théorie quantique des champs que le spin montre son caractère le plus fondamental. L'analyse du groupe de Poincaré effectuée par Wigner en 1939 montra en effet qu'une particule est associée à un champ quantique, opérateur qui se transforme comme une représentation irréductible du groupe de Poincaré. Ces représentations irréductibles se classent par deux nombres réels positifs : la masse et le spin.
" Rotation propre "
Historiquement, le spin a d'abord été interprété par Uhlenbeck et Goudsmit en septembre 1925[1] [UG25] comme étant un moment cinétique intrinsèque, c'est-à-dire comme si la particule " tournait sur elle-même ". Cette vision classique d'une " rotation propre " de la particule est en fait trop naïve ; en effet :
- si la particule est ponctuelle, la notion de rotation propre autour de son axe est tout simplement dénuée de sens physique.[2]
- si la particule n'est pas ponctuelle, alors la notion possède un sens, mais on se heurte dans ce cas à une autre difficulté.[3] Supposons par exemple que la particule soit un électron, modélisé comme étant un corps sphérique de rayon a. On obtient une estimation du rayon a en écrivant que l'énergie de masse de l'électron est de l'ordre de grandeur de son énergie potentielle électrostatique, soit :
|
|
- La valeur numérique de ce " rayon classique " de l'électron est :
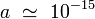
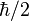
|
|
- La valeur numérique vaudrait :
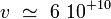
Interprétation physique du spin
Opérateur spin
En mécanique quantique, le spin est un opérateur vectoriel hermitien comportant trois composantes, notées usuellement
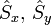
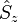
où εijk est le symbole de Levi-Civita. Ces relations de commutations sont analogues à celles découvertes en novembre 1925 par Born, Heisenberg et Jordan pour les composantes du moment cinétique orbital :
![\left[ \, \hat{L}_i \, , \ \hat{L}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{L}_k](https://static.techno-science.net/illustration/Definitions/autres/5/50b2055de1bf66ce973994caf003e045_e524276fd2acaeceb4bef62a2b48319c.png)
Par analogie avec les résultats obtenus pour le moment cinétique orbital (ou plus généralement pour un moment cinétique quantique), il existe pour l'opérateur spin une base de vecteurs propres notés | s,ms > , où s est entier ou demi-entier, et ms est un entier ou demi-entier prenant l'une des 2s + 1 valeurs
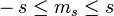
Spin 1/2 - matrices de Pauli
Pour une particule de spin 1/2 comme l'électron, on a s = 1 / 2, donc 2s + 1 = 2 : il existe seulement deux états de spin distincts, caractérisés par
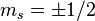
On note souvent les deux états propres correspondant :
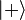
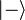
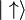
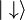
Pauli a introduit trois matrices 2 x 2, notées
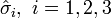
Ces trois matrices de Pauli s'écrivent explicitement :
Elles satisfont les relations de commutation :
Représentation géométrique du spin par une sphère de Riemann
Un état quantique quelconque d'une particule de spin 1/2 peut s'exprimer sous la forme générale :
(a et b étant deux nombres complexes). Cette formule exprime une superposition des deux états propres.
Selon les règles de la mécanique quantique, l'état quantique représenté par

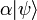
L'état de spin 1/2 est donc entièrement caractérisé par un nombre complexe
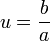
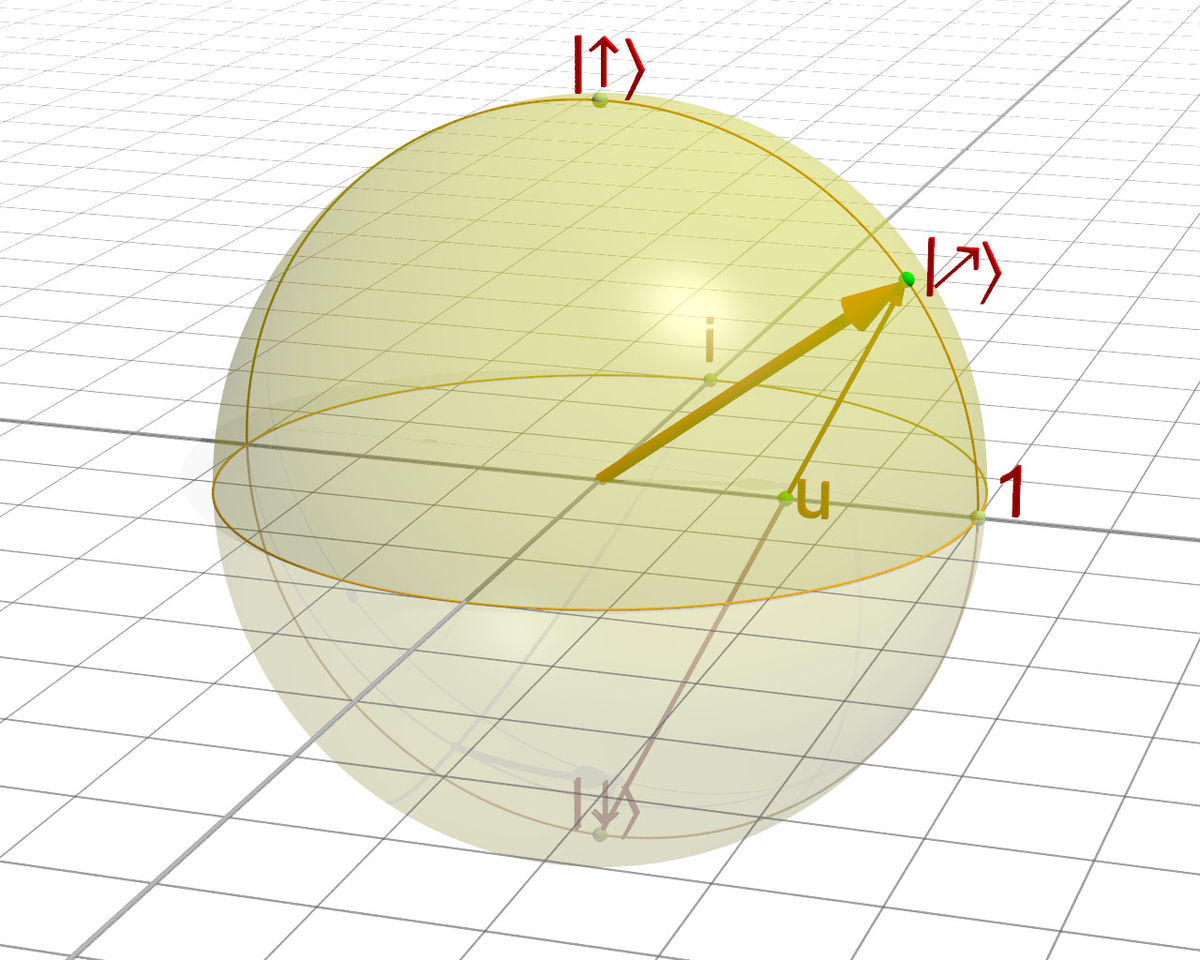
Selon cette représentation, tout état de spin 1/2 trouve une représentation géométrique (voir figure ci-contre). Le vecteur passant par l'origine et pointant sur la projection du complexe u sur la sphère de Riemann donne une visualisation géométrique de l'état de spin 1/2 comme étant une direction dans l'espace.
Bien que semblant a priori purement mathématique, cette représentation de l'état de spin comme étant une direction dans l'espace possède une certaine pertinence. Notamment, on peut retrouver simplement à l'aide de cette représentation géométrique la probabilité d'obtenir l'état
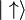
Moment magnétique de spin
Définition. Facteur de Landé
Au moment cinétique orbital d'une particule de charge q et de masse m est associé un moment magnétique orbital :
Le facteur q / 2m est appelé rapport gyromagnétique. De même, on associe à une particule de charge q, de masse m, et de spin donné un moment magnétique de spin :
où g est un nombre sans dimension, appelé facteur de Landé (1921). Ce nombre varie selon la nature de la particule : on a approximativement g = 2 pour l'électron, g = 5,586 pour le proton, et
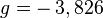
Magnéton de Bohr
Pour l'électron, on a les valeurs suivantes :
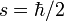
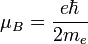
Moment magnétique anormal de l'électron
L'équation de Dirac prédit pour l'électron un facteur de Landé exactement égal à : g = 2. Or, la valeur expérimentale admise en 2005 vaut :
Il existe donc un écart, décelé pour la première fois en 1947 dans la structure hyperfine de l'hydrogène et du deutérium [KN02] : on parle alors du moment magnétique anormal de l'électron. La théorie quantique des champs du modèle standard permet de rendre compte de cette anomalie avec une très grande précision.
Notes et références
- ↑ Un problème de facteur 2 dans la structure fine du spectre de l'hydrogène, identifié par Heisenberg, fut résolu en décembre 1925 avec l'aide d'Einstein, sous l'impulsion de Bohr. Ce dernier demanda à deux physiciens hollandais de publier le résultat en urgence : S. Goudsmit et G.E. Uhlenbeck ; Nature 117 (1926) 264.
- ↑ Par définition, l'axe de rotation d'un objet est le lieu de points de cet objet qui restent immobiles. Si la particule est ponctuelle, son axe propre est sur la particule, donc celle-ci est immobile.
- ↑ Il faudrait aussi expliquer quelles sont les forces internes qui assurent le cohésion de cet électron étendu. Ce problème a occupé un grand nombre de théoriciens dans les années 1895 à 1930, avant que l'électrodynamique quantique et son électron ponctuel ne deviennent bien établies.
- ↑ Bien que le neutron ait une charge q = 0, on lui attribue ici un facteur de Landé correspondant au moment magnétique de spin calculé pour la valeur q = e, afin de le comparer à ceux de l'électron et du proton.
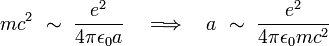
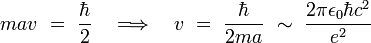
![\left[ \, \hat{S}_i \, , \ \hat{S}_j \, \right] \ = \ i \ \hbar \ \epsilon_{ijk} \ \hat{S}_k](https://static.techno-science.net/illustration/Definitions/autres/5/56736a4c37a2470ddb3bc4bf03c15bab_cad961c5e0499e2ad612700161c13ae0.png)
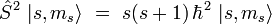
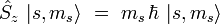
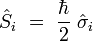
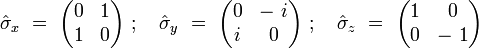
![\left[ \, \hat{\sigma}_i \, , \ \hat{\sigma}_j \, \right] \ = \ 2 \ i \ \epsilon_{ijk} \ \hat{\sigma}_k](https://static.techno-science.net/illustration/Definitions/autres/f/f0e84d8251c96b1f008b317be9a55e54_cf13755f1854e8e64745a5d1e50a84b7.png)