Principe d'incertitude - Définition

Articles de physique quantique |
| Théorie quantique |
| Électrodynamique quantique |
| Mécanique quantique |
| Théorie des champs |
| Modèle standard |
| Statistiques quantique |
| Bose-Einstein |
| Fermi-Dirac |
| Maxwell-Boltzmann |
| Physiciens |
| Bohr - de Broglie |
| Bose - Einstein |
| Fermi - Dirac |
| Heisenberg - Pauli |
| Schrödinger - Feynman |
Le principe d'indétermination fut énoncé au printemps 1927 par Heisenberg lors des balbutiements de la mécanique quantique.
Les travaux de Planck, Einstein et De Broglie avaient mis à jour que la nature quantique de la matière entraînait l'équivalence entre des propriétés ondulatoires (fréquence et vecteur d'onde) et corpusculaires (énergie et impulsion) selon les lois :
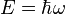
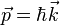
La dualité onde-corpuscule confirmée alors par de nombreuses expérimentations posait un problème de fond aux physiciens. En effet, pour posséder une fréquence et un vecteur d'onde, un objet doit avoir une certaine extension en espace et en temps. Un objet quantique ne peut donc être ni parfaitement localisé, ni avoir une énergie parfaitement définie.
De manière simplifiée, ce principe d'indétermination énonce donc que — de façon assez contre-intuitive du point de vue de la mécanique classique — pour une particule massive donnée, on ne peut pas connaître simultanément sa position et sa vitesse. Soit on peut connaître précisément sa position (par ex: à ± 1 mm) contre une grande incertitude sur la valeur de sa vitesse (par ex: à ± 100 m/s), soit on peut connaître précisément sa vitesse (par ex: à ± 0,0001 m/s) contre une grande incertitude sur la valeur de sa position (par ex: à ± 1 km).
Cependant, si on renonce à considérer la particule en tant qu'objet corpusculaire, l'énoncé de ce principe devient plus intuitif. L'objet quantique ayant une certaine extension dans l'espace et une certaine durée de vie en temps, on le représente alors, non plus par un ensemble de valeurs scalaires (position, vitesse), mais par une fonction décrivant sa distribution spatiale. Toute l'information relative à la particule est contenue dans cette fonction d'onde. Les mesures scalaires effectuées sur cette particule consistent à extraire seulement une partie de cette information, par l'intermédiaire d'opérateurs mathématiques.
Historique du terme
Le principe d'incertitude est souvent appelé principe d'indétermination. L'emploi de ces deux termes pour désigner la même notion résulte d'un problème lors de la traduction en anglais de l'article de Heisenberg. En effet, lors de la première rédaction de son article, Heisenberg emploie les termes Unsicherheit (incertitude) et Ungenauigkeit (imprécision), puis, comprenant que ces termes peuvent prêter à confusion, il décide d'utiliser finalement le terme Unbestimmtheit (indétermination). Mais l'article est déja traduit et c'est le terme "principe d'incertitude" qui sera consacré.[1]
En raison de ces connotations philosophiques, aujourd'hui les physiciens parlent des relations d'incertitude, ou des inégalités de Heisenberg, car il s'agit d'une inégalité portant sur des grandeurs physiques non-commutatives.
Les relations de Heisenberg
Considérons une particule massive non relativiste se déplaçant sur un axe.
Description classique
La mécanique classique de Newton affirme que la dynamique de la particule est entièrement déterminée si l'on connaît à chaque instant : sa position x et sa quantité de mouvement p = mv (également appelée : impulsion). Ces deux grandeurs physiques réelles ont des valeurs appartenant à



Description quantique
L'immense effort intellectuel qu'a représenté l'accouchement de la mécanique quantique [VN46] réside dans le fait suivant : " il faut abandonner la logique d'Aristote ". La logique quantique, sans notion de tiers-exclu, vient la remplacer.
Cela dit, le paradoxe n'est qu'apparent. Il vient du fait que les grandeurs scalaires classiques sont insuffisantes pour décrire la réalité quantique. On doit faire appel à des fonctions d'onde qui sont des vecteurs appartenant à un espace de Hilbert de dimension infinie.
Les grandeurs classiques ne sont donc en fait que des vues partielles de l'objet, potentiellement corrélées.
Notion d'observable
Très curieusement, une grandeur physique, appelée une observable, n'est plus une fonction f (x,p) réelle, mais est représentée par un opérateur hermitien
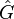

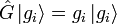
Si l'état du système à l'instant de la mesure est un vecteur


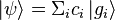
où les ci sont des nombres complexes.
Interprétation probabiliste
Le nombre complexe ci permet de calculer la probabilité pi d'obtenir la valeur gi :
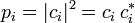
La mesure de la grandeur est donc une variable aléatoire (v.a.) avec une espérance E(g) et un écart type σ(g) [3]. La mesure est donc de nature probabiliste, ce qui implique beaucoup de paradoxes apparents en logique aristotélicienne. L'un d'entre eux a été immédiatement remarqué par Heisenberg : comme l'opérateur position

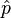
![\left[ \hat{q} , \hat{p} \right] = i \, \hbar \,\hat{\Bbb{I}}](https://static.techno-science.net/illustration/Definitions/autres/7/7a55238103043d11b06bc2325aac9c5f_a7ee5e8a4e391c60ebd1b80a478a310f.png)
on ne peut pas mesurer simultanément ces deux grandeurs : la notion d'espace des phases disparaît en mécanique quantique. L'objet quantique est en fait complètement décrit par sa fonction d'onde. Les grandeurs scalaires utilisées en physique classique sont insuffisantes et inadéquates.
L'évolution déterministe de Newton est remplacée par une équation d'évolution déterministe de Schrödinger, permettant de prédire de façon certaine l'évolution temporelle des fonctions d'onde (dont le module carré est la probabilité, la phase n'étant pas connue a priori).
Inégalité de Heisenberg
Des mesures répétées de la position et de l'impulsion donneront des résultats en général différents à chaque mesure : chaque échantillon de valeurs sera caractérisé par un écart type : σx pour la position, et σp pour l'impulsion. Le théorème de Heisenberg démontre que :
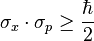
où

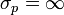
Principe général de Heisenberg
Le théorème de Heisenberg ne s’applique pas seulement au couple de valeurs position et quantité de mouvement. Dans sa forme générale, il s’applique à chaque couple d'opérateurs

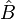
Énoncé du principe de Heisenberg
Pour un état

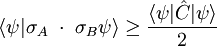
où la valeur moyenne du commutateur
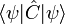

Ce théorème général, conséquence de l’inégalité de Cauchy-Schwarz, fut mis en évidence en 1930 par Robertson et (indépendamment) par Schrödinger ; l'inégalité est donc aussi connue comme la relation de Robertson-Schrödinger.
Principe ou théorème ?
Les puristes réservent parfois le nom de principe au cas où un minorant non nul de
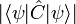

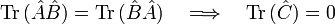
Il n'y a alors que théorème d'Heisenberg, et non pas principe ; c'est par exemple le cas d'un spin 1/2.
Autre formulation du principe de Heisenberg
L'inégalité de Heinseberg est souvent écrite :
![\Delta{A} \cdot \Delta{B} \ge \frac{1}{2} \left| \left\langle \left[ \hat{A}, \hat{B} \ \right] \right\rangle_\gamma \right|](https://static.techno-science.net/illustration/Definitions/autres/7/7cb2703eac36a28d1371aec39fb4f194_f49520ea2e338fb5dc1c842d7ec34737.png)
où :
- A et B sont deux observables,
-

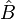
-
![[\hat{A},\hat{B}]](https://static.techno-science.net/illustration/Definitions/autres/c/c081d8bf21108f8283f018b863a75393_ebf9d1eeea34da9e2be0c39b3e1aae8b.png)

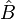
-
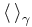
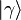
- Δ X est l’écart type de X :
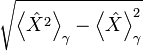
Relation temps-énergie
Il existe également une relation d'incertitude portant sur l'énergie d'un particule et la variable temps. Ainsi, la durée Δt nécessaire à la détection d'une particule d'énergie E à ΔE près[4] vérifie la relation :
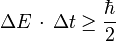
Cependant, la déduction de cette inégalité énergie-temps est assez différente de celle des inégalités position-impulsion[5]. En effet, si le Hamiltonien est bien le générateur des translations dans le temps en mécanique hamiltonienne, indiquant que temps et énergie sont conjugués[6], il n'existe pas d'opérateur temps en mécanique quantique (" théorème " de Pauli), c’est-à-dire qu'on ne peut pas construire d'opérateur
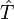
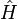
![\left[ \hat{H} , \hat{T} \right] = i \hbar \hat{\Bbb{I}}](https://static.techno-science.net/illustration/Definitions/autres/f/f34f47b6cc3414bcd9345b4893806846_791a838563b47ed7498060a189dc94d9.png)
ceci pour une raison très fondamentale : la mécanique quantique a en effet été inventée pour que chaque système physique stable possède un état fondamental d'énergie mininum[7].
Perspective historique
Il est clair que l'abandon de la logique d'Aristote à cause de la nature probabiliste de la mesure a suscité un vif émoi dans la communauté scientifique : John von Neumann est un des tous premiers à écrire sur la logique quantique [BVN36], suivi par Mackey [MA63].
La controverse Einstein-Bohr est par ailleurs célèbre : pour Einstein, " Dieu ne joue pas aux dés ! ", ce à quoi Bohr répondra : " Einstein, cessez de dire à Dieu ce qu'Il doit faire ". Le paradoxe EPR entraînera Bell via ses inégalités à renoncer à la notion classique de localité [BE64]. Cette hypothèse sera confirmée par l'expérience d'Aspect en 1982 ; cette expérience sera encore raffinée par Zeilinger en 1998 [AS01]. Le paradoxe du chat de Schrödinger conduira à une réflexion profonde sur le rôle du couplage à l'environnement et la décohérence des intricats [HA97], [OM00], [IHP05]. D'où la progression fulgurante de la cryptologie quantique, de la téléportation quantique, réalités techniques en 2005, et de l'informatique quantique, encore balbutiante en 2005.
Difficulté d'interprétation
Exemples
Cette corrélation d'incertitudes est parfois expliquée de manière erronée en affirmant que la mesure de la position modifie obligatoirement la quantité de mouvement d'une particule. Heisenberg lui même offrit initialement cette explication en 1927. Cette modification ne joue aucun rôle, car le théorème s'applique même si la position est mesurée dans une copie du système, et la quantité de mouvement dans une autre copie parfaitement identique.
Une meilleure analogie serait la suivante : soit un signal variable dans le temps, comme une onde sonore, et soit à connaître la fréquence exacte de ce signal à un instant t précis. Ceci est impossible en général, car pour déterminer précisément la fréquence, il faut échantillonner le signal pendant une certaine durée [8]. En traitement du signal, cet aspect est au cœur de l'approche temps-fréquence du spectrogramme où l'on utilise le principe d'incertitude sous la formulation de Gabor.
Le théorème d'Heisenberg s'applique en particulier à l'expérience cruciale des fentes d'Young avec un photon unique : toutes les ruses qu'inventent les physiciens pour tenter de voir passer la "particule" à travers un des trous, détruisent la phase et donc les interférences de l'onde : il y a complémentarité de Bohr, c’est-à-dire que si avant toute mesure , l'état quantique | ψ > décrit à la fois un aspect ondulatoire et un aspect corpusculaire, après la mesure , il subsiste un aspect ondulatoire ou un aspect corpusculaire. Selon la phrase célèbre de Dirac , la " particlonde[9] " a interféré avec elle-même.
Cette expérience est présentée au Palais de la Découverte avec une source de photon unique. Le motif produit par des millions de photons passant à travers les fentes peut être calculé à l'aide de la mécanique quantique, mais le chemin de chaque photon ne peut être prédit par aucune méthode connue. L'interprétation de Copenhague dit qu'il ne pourra être calculé par aucune méthode. En 2005, on a même réussi cette expérience avec des fullerènes, ces grosses molécules de carbone contenant 60 atomes !
La controverse Bohr-Einstein
Einstein n'aimait pas le théorème d'incertitude. Lors du 5ème congrès Solvay (1927), il soumit à Bohr un fameux défi expérimental : nous remplissons une boîte avec un matériau radioactif qui émet de manière aléatoire une radiation. La boîte a une fente qui est ouverte et immédiatement fermée par une horloge de précision, permettant à quelques radiations de sortir. Donc le temps est connu avec précision. Nous voulons toujours mesurer précisément l'énergie qui est une variable conjuguée. Aucun problème, répond Einstein, il suffit de peser la boîte avant et après. Le principe d'équivalence entre la masse et l'énergie donnée par la relativité restreinte permet ainsi de déterminer précisément l'énergie qui a quitté la boîte. Bohr lui répondit ceci : si de l'énergie avait quitté le système alors la boîte plus légère serait montée sur la balance. Ce qui aurait modifié la position de l'horloge. Si l'horloge dévie de notre référentiel stationnaire, par la relativité restreinte il s'ensuit que sa mesure du temps diffère de la notre, ce qui conduit inévitablement à une marge d'erreur. En fait l'analyse détaillée montre que l'imprécision est donnée correctement par la relation d'Heisenberg. Voir par exemple le site de la fondation Nobel pour une figure de cette " horloge dans la boîte ".
Dans l'interprétation de Copenhague de la mécanique quantique, largement acceptée mais pas universellement, le théorème d'incertitude implique qu'à un niveau élémentaire, l'univers physique ne " vit " pas dans un espace des phases, mais plutôt comme un ensemble de réalisations potentielles, exactement déterminées en probabilité : les probabilités sont, elles, déterminées avec une précision absolue, pour autant que l'état du système soit pur (c’est-à-dire qu'il ne soit pas lui-même déterminé approximativement !)
États comprimés
En fait , pour contourner les inégalités d'Heisenberg, les physiciens réalisent des états dits comprimés (en franglais : états " squeezés "), où il n'y a aucune incertitude sur la phase (mais alors le nombre de particules est indéterminé) ou, au contraire, un nombre bien déterminé de particules (en particulier de photons), mais on perd l'information sur la phase. Il a été montré par les travaux de Glauber (prix Nobel 2005) que l'information quantique n'est pas entachée par le théorème d'Heisenberg. On peut donc espérer tirer le maximum d'information quantique d'une photographie numérique, tout en respectant le deuxième principe de la thermodynamique[10].
Claustrophobie quantique
Définition
La claustrophobie quantique est la tendance qu'ont les particules à vibrer frénétiquement lorsqu'elles sont confinées dans un milieu très petit. Les systèmes deviennent fluctueux à des échelles microscopiques.
Constante de Planck
Les fluctuations de ces systèmes sont de l'ordre de 10-33, autrement dit, la constante de Planck notée
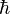
Conséquences
Cela veut dire, que si ? était plus grand, ces comportements turbulents se manifesteraient non plus à des échelles subplanckienne mais aux échelles macroscopiques. Deux dés dans une boîte se mettraient à virevolter frénétiquement si la constante de Planck était plus élevée.
Interprétations philosophiques du principe d'incertitude
Le sens des mots
Pour mieux comprendre le débat qui a suivi l'introduction de ces relations d'indétermination, il importe de préciser le sens des mots .
"Déterminer" signifie fixer, définir ((de) : bestimmen, (en) : determine). Ceci peut être réalisé avec plus ou moins de précision ((de) : Genauigkeit, (en) : precision), ce qui n'est pas tout à fait la même chose que certitude ((de) : Sicherheit, (en) : certainty).
En fait, les deux dernières notions s'opposent parfois : si une grandeur est mesurée avec une certaine imprécision autour d'une valeur, on sera d'autant plus certain de la situer dans une fourchette autour de cette valeur que cette fourchette est large. Mais évidemment, prendre une fourchette large correspond à une mauvaise précision. Par exemple, on estime classiquement que l'erreur de mesure, qui correspond à une grande multiplicité de facteurs possibles est une variable aléatoire gaussienne, dont on est censé capable d'estimer l'écart type. Si l'on prend une fourchette de 1 écart-type de part et d'autre de la valeur mesurée, on a une probabilité de 68% d'être dans le vrai, ce qui correspond à une faible certitude ; pour 2 écarts-types, on a 95%, ce qui se rapproche d'une bonne certitude, pour 3, on a 99,7%, ce qui commence à faire une certitude solide, au prix d'une précision relativement floue. Comme en fait l'écart-type n'est pas aussi bien connu qu'on le souhaiterait, on se contente souvent d'une précision de 2 écarts-types de part et d'autre de la valeur mesurée, et d'une certitude de 95%. On compte sur les progrès des techniques, la diversité des méthodes, et l'expérience accumulée pour préciser les conclusions.
"Indéterminé" veut donc dire imprécis, indéfini ou mal défini, flou, vague, indécis, irrésolu ; dont les limites ne sont pas précisément définies; se dit en mathématiques de systèmes dont au moins l'une des données est inconnue ou aléatoire ((de) : unbstimmt, (en) : undetermined).
On parle aussi de motif déterminant, ou d'une cause déterminante, qui décide d'une chose ou d'une action, élément déclenchant d'un phénomène physique, donc essentiel, décisif, prépondérant, et surtout cause d'un comportement subséquent unique. D'où le débat sur "causalité" et "déterminisme".
Quant à l'incertitude, c'est le caractère d'imprécision d'une mesure, d'une conclusion, le vague d'une perception ou d'une image, l'imprévisibilité du résultat d'une action ou d'une évolution, l'impossibilité de prévoir exactement un fait ou un événement.
L'incertitude désigne aussi la quantité mesurant la limite de l'erreur éventuelle pouvant affecter une mesure: c'est initialement dans ce sens technique que ce mot a été utilisé pour désigner les quantité Δq, Δp et leur produit.
L'interprétation subjective: l'incertitude
Heisenberg, Born, et avec eux toute l'école de Copenhague, ont insisté sur le fait que les relations d'indétermination causent une incertitude sérieuse pour l'observateur, particulièrement les physiciens qui s'appuient sur l'expérimentation. Ils ont souligné l'impossibilité de connaître à la fois la position et la vitesse ou la quantité de mouvement d'une particule, et que l'instrument utilisé pour mesurer agit sur le corpuscule et donc le modifie.
" Ces relations indiquent les limites à l'intérieur desquelles la théorie corpusculaire est applicable. Employer les mots “position”, “vitesse” avec une précision dépassant les limites imposées par l'équation n'a pas plus de valeur qu'employer des mots dont le sens n'a pas été défini. (…) "
Les expériences destinées à la détermination d'une grandeur physique rendent illusoire la connaissance d'autres grandeurs, car elles perturbent d'une manière incontrôlable le système en observation, et, par suite, modifient les valeurs des grandeurs antérieurement déterminées... Les relations d'indétermination se rapportent au degré de précision possible pour la connaissance présente des valeurs simultanées de diverses grandeurs de la théorie des quanta" (Heisenberg, idem).
Lois à caractère statistique
Une conséquence majeure fut que les lois de la microphysique ont alors pris une tournure statistique. Les ondes de matière qui décrivaient les quanta devinrent des ondes de probabilité.
Congrès Solvay, 1927 : " Les discontinuités introduisent dans la physique de l'atome un élément statistique. Cet élément statistique constitue une partie essentielle des bases de la mécanique des quanta ; d'après celle-ci, l'allure d'une expérience, dans beaucoup de cas, ne peut être déduite des conditions initiales que d'une manière statistique... La mécanique des quanta représente un fusionnement de la mécanique et de la statistique. "
Pauli à Heisenberg : " En opposition avec tous les efforts rétrogrades (Schrödinger, Bohm et dans un certain sens Einstein), je suis persuadé que le caractère statistique de la fonction ψ, et par suite des lois de la nature, que vous avez dès l'origine soutenu énergiquement contre l'avis de Schrödinger, détermineront le style de toutes les lois pour au moins quelques siècles".
Excès de l'interprétation subjective
Pour le physicien qui étudiait les éléments encore peu connus de la microphysique, il était prudent de s'en tenir au point de vue subjectif (celui du sujet qui mesure) sans trop se soucier de la nature intime des corpuscules qui reste hors d'atteinte (l'objet observé). Et il reste vrai que, encore aujourd'hui, cette mécanique statistique demeure la plus efficace.
Cependant des excès ont affaibli cette école :
- Exagération de l'importance de l'indétermination au point de nier la notion de trajectoire, alors que les écarts restent petits et qu'ils se compensent en partie.
- Exagération de l'interférence entre l'instrument de mesure et l'objet mesuré, qui masque que l'indétermination puisse être objective.
- Exagération de l'opposition entre sujet et objet. Postulat de séparation entre observateur et observé (nourri de Kant). Tendance à couper la microphysique des lois macroscopiques. Finalement, idéologie de l'inconnaissabilité du monde.
- Refus d'étudier le comportement d'une particule individuelle, au point que seule la considération des flux serait légitime : " Tout essai pour pénétrer dans le mécanisme des relations entre ondes et particules… serait inutile et dénué de sens " (Dirac). A quoi de Broglie rétorque que sa théorie de l'onde-pilote " a le mérite d'exister alors que (ce) raisonnement… a la prétention de lui interdire d'exister ".
L'interprétation objective
Einstein et de Broglie ont très tôt marqué leur insatisfaction de l’interprétation de l'équipe Born-Heisenberg, et la tendance serait aujourd'hui à reconnaître le caractère objectif de l'indétermination, par exemple que l'onde de lumière positionne effectivement ses photons de part et d'autre de l'axe de la trajectoire, aléatoirement.
De Broglie : de la fonction préalablement "normée" " on a cru pouvoir conclure que l'électron était présent à l'état potentiel dans tout l'atome avec probabilité. Mais comme l'électron est certainement une très petite particule dont on connaît les dimensions très inférieures à celle de l'atome, une telle affirmation n'est pas acceptable. C'est comme si je disais que telle personne, dont je connais les habitudes et qui a telle ou telle probabilité de se trouver actuellement dans tel ou tel quartier de Paris, était répandue à l'état potentiel dans toute la ville ! La seule manière raisonnable d'interpréter le fait qui paraît prouvé que l'électron a une certaine probabilité d'être présent à un point quelconque de l'atome d'hydrogène est d'admettre qu'il est constamment animé d'un mouvement brownien qui le fait se déplacer continuellement et aléatoirement dans tout l'atome."
Einstein: " Il y a quelque chose qui est l'état réel d'un système physique, qui existe objectivement, indépendamment de toute observation ou mesure, et qui peut en principe se décrire par les moyens d'expression de la physique. " Mais on ne saurait interpréter sa boutade " Dieu ne joue pas aux dés " comme un rejet de toute indétermination (il disait aussi que " la gravitation ne peut être tenue responsable du fait que les êtres humains tombent amoureux "), mais comme l'exigence d'une analyse des causes plus détaillée que la description statistique de flux.
Trois points principaux dans ce débat :
- À l'indétermination observée par le sujet qui mesure, correspond une détermination aléatoire par l'onde de matière elle-même. L'incertitude n'est qu'une conséquence. Ce sont les ondes de matière qui positionnent des corpuscules avec une relative indétermination.
- L'indétermination provient du caractère discontinu de la matière qui, ne pouvant diviser un quantum élémentaire, dans les cas de division indéfinie nécessairement aura un plus ou un moins.
- Nul besoin de connaître précisément son mode opératoire pour admettre que l'onde détermine les positions et vitesse de ses corpuscules de façon variable. Il suffit d'admettre qu'elle se détermine "tant qu'elle peut" (comme nous faisons nous-mêmes dans nos comportements).
Excès de l'interprétation objective
L'excès consisterait à croire que d'éventuelles découvertes nouvelles pourraient dissoudre la dimension aléatoire. Heisenberg disait que le mode d'existence des particules n'est pas identique à celui des objets macroscopiques. De l'énergie potentielle qui devient onde de matière, puis corpuscule durable, puis atome, il y a des degrés dans l'évolution de la matière.
Déterminisme et causalité
Les relations d'indétermination ont engendré une profusion d'écrits mettant en question le déterminisme et (ce qui est plus grave) le principe de causalité.
On est passé d'une conception ultra déterministe de la science (voir citation de d'Holbach dans Déterminisme) à une négation de toute causalité. Par exemple :
Max Born : " Il est clair que le dualisme onde-corpuscule et l'incertitude essentielle qu'il implique nous obligent à abandonner tout espoir de conserver une théorie déterministe. La loi de causalité... n'est plus valable, du moins plus au sens de la physique classique. Quant à la question de savoir s'il existe encore une loi de causalité dans la nouvelle théorie, deux points de vue sont possibles. Soit on persiste à envisager les phénomènes à l'aide des images d'onde et corpuscule, alors la loi de causalité n'est certainement plus valable... La loi de causalité est donc sans contenu physique ; la nature des choses impose que la physique soit indéterministe ".
John von Neumann : " En physique macroscopique, aucune expérience ne peut prouver la causalité, car l'ordre causal apparent n'y a pas d'autre origine que la loi des grands nombres, et cela tout à fait indépendamment du fait que les processus élémentaires, qui sont les véritables processus physiques, suivent ou non des lois causales... C'est seulement à l'échelle atomique, dans les processus élémentaires eux-mêmes, que la question de la causalité peut réellement être mise à l'épreuve : mais à cette échelle, dans l'état actuel de nos connaissances, tout parle contre elle, car la seule théorie formelle s'accordant à peu près avec l'expérience et la résumant est la mécanique quantique, qui est en conflit logique avec la causalité... Il ne subsiste aujourd'hui aucune raison permettant d'affirmer l'existence de la causalité dans la nature ".
Ces positions sont excessives car, si des causes identiques pouvaient produire des effets vraiment différents, il ne pourrait y avoir ni science (qui est la reconnaissance des causes invariantes), ni règles et, sans doute, ni homme ni rien de stable.
Deux notions ont été confondues qui ne se recouvrent pas exactement. La causalité n'implique pas qu'une même cause génère des effets rigoureusement identiques et absolument uniformes, avec une précision infinie tant de la cause que de l'effet. Mais c'est ce que suppose l'idéologie du Determinismus qui nie toute possibilité d'écart, de marge de manœuvre, de liberté.
Ce déterminisme est la causalité plus l'hypothèse supplémentaire de continuité, d'enchaînements strictement continus qui seuls pourraient produire des choses absolument en tous points identiques. Cette conception s'était insinuée avec l'idéal mathématique, où la continuité et l'infini servent à abréger le raisonnement, et avec les idées de Newton qui postulait que " la nature ne connaît pas de limites ". L'introduction de la discontinuité fondamentale (le quantum de Planck) a ruiné cette continuité idéale, et l'indétermination partielle qui en découle a ruiné le déterminisme mécaniste d'automate. Mais le principe de causalité simple demeure.
Il reste que le principe d'incertitude interdit de déterminer avec une précision arbitraire à la fois le module et la phase de la fonction d'onde, dans quelque représentation que ce soit. Or les deux sont nécessaires pour prévoir l'évolution d'un système. La causalité —exprimée par exemple par l'équation de Schrödinger— ne nous permet pas d'atteindre à une conséquence pratique.
Indétermination et liberté
" Est dite libre la chose qui existe d'après la seule nécessité de sa nature et qui détermine elle-même son action. A l'inverse on appelle nécessaire, ou plutôt contrainte, la chose qui est déterminée par une autre à exister et à produire un effet selon une raison définie et déterminée " (Spinoza).
A quoi s'ajoute ces remarques de Lucrèce, qui avait compris la limitation de la représentation mécaniste et la nécessité d'écarts. Son fameux clinamen, qui introduit la liberté que tout strict mécanisme exclut, correspond à l'indétermination quantique, comme on le voit quand on traduit atome par corpuscule :
" Les corpuscules descendent en ligne droite… mais il leur arrive, on ne saurait dire où ni quand, de s'écarter un peu de la verticale, si peu qu'à peine on peut parler de déviation. Sans cet écart ils ne cesseraient de tomber… il n'y aurait point lieu à rencontres, à chocs, et jamais la nature n'aurait rien pu créer... C'est pourquoi il faut que les corpuscules s'écartent un peu de la verticale, mais à peine et le moins possible. (...)
Qu'un rien le dévie de sa ligne, qui serait capable de s'en rendre compte ? Mais si tous les mouvements sont enchaînés dans la nature, si toujours d'un premier naît un second suivant un ordre rigoureux, si par leurs écarts les corpuscules ne provoquent pas un mouvement qui rompe les lois de la fatalité, et qui empêche que les causes ne se succèdent à l'infini, d'où viendrait donc cette liberté accordée sur terre aux êtres vivants ; d'où viendrait, dis-je, cette libre faculté arrachée au destin, qui nous fait aller partout où la volonté nous mène ? (...)
Aux corpuscules aussi nous devons reconnaître cette propriété : eux aussi ont une cause de mouvement autre que les chocs et la pesanteur — une cause d'où vient le pouvoir inné de la volonté, puisque nous voyons que rien ne peut naître de rien... Or tel est l'effet d'une légère déviation des corpuscules, dans des lieux et des temps non déterminés. "
Ces réflexions doivent cependant être mises en balance avec le fait qu'il nous est impossible tant de déterminer l'état initial de l'Univers, que de calculer le comportement d'un univers déterministe qui nous contient, même si on en connaissait parfaitement l'état initial et les lois exactes d'évolution. Nous sommes donc condamnés à vivre dans un monde imparfaitement connu, et donc incapables d'y déterminer les poids relatifs du hasard, de la nécessité et de la liberté.
Notes
- ↑ Jean-Marc Lévy- Leblond et Françoise Balibar, When did the indeterminacy principle become the uncertainty principle ?, Physics 66, 1998, p. 278- 279, cité par Etienne Klein dans (lien) page 6
- ↑ On note gi la valeur propre associée au vecteur propre
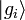
- ↑ Plus généralement, tous les moments peuvent être définis.
- ↑ Ce concept est primordial en théorie quantique des champs, théorie qui fait appel à la notion de particule virtuelle.
- ↑ Pour une dérivation rigoureuse de l'inégalité énergie-temps, consulter par exemple : Albert Messiah Mécanique quantique - volume 1, Dunod (1959) p. 114-117, p. 269-270, et enfin, pour l'oscillateur harmonique, p. 280. Ouvrage réédité par Dunod en 1995 : ISBN 2100073613.
- ↑ De même que la composante pi de l'impulsion est le générateur des translations d'espace dans la direction xi.
- ↑ L'argument de Pauli est le suivant : si l'opérateur temps existait, il posséderait un spectre continu. Or, l'opérateur temps, obéissant à la relation de commutation canonique, serait aussi le générateur des translations en énergie. Ceci entraîne alors que l'opérateur hamiltonien posséderait lui aussi un spectre continu et infini dans les deux sens, en contradiction avec le fait que l'énergie de tout système physique stable se doit d'être bornée inférieurement. Concernant la validité de ce " théorème ", lire les travaux très récents d'Eric Galapon : quant-ph/9908033 et quant-ph/0303106.
- ↑ Techniquement, le temps et la fréquence sont ici des variables conjuguées au sens de la transformée de Fourier.
- ↑ Jean-Marc Lévy-Leblond a proposé d'utiliser plutôt le terme de quanton : Jean-Marc Lévy-Leblond & Françoise Balibar ; Quantique : rudiments, InterEditions/Editions du CNRS (1984). Réédité par Masson (1997) ISBN 2-225-85521-8, aujourd'hui racheté par Dunod : ISBN 2-225-85521-8.
- ↑ Voir par exemple les travaux de Claude Fabre (Laboratoire Kastler-Brossel, université Paris 6).
- ↑ Ici nous ne parlons que de la constante de Planck réduite (voir Constante de Planck)

















































