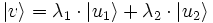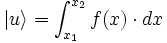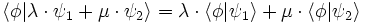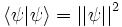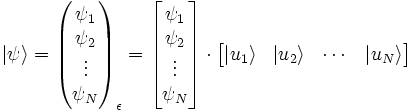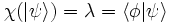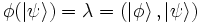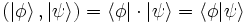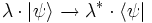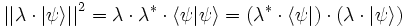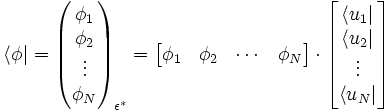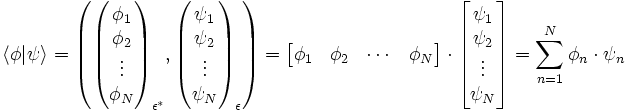Dimanche 27 Avril 2025
Rechercher 🔍
Physique

Notation bra-ket - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Articles de
physique quantique
Théorie quantique
Électrodynamique quantique
Mécanique quantique
Théorie des champs
Modèle standard
Statistiques quantique
Bose-Einstein
Fermi-Dirac
Maxwell-Boltzmann
Physiciens
Bohr - de Broglie
Bose - Einstein
Fermi - Dirac
Heisenberg - Pauli
Schrödinger - Feynman

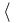
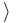
La notation bra-ket a été introduite par Paul Dirac pour faciliter l’écriture des équations de la mécanique quantique, mais aussi pour souligner l’aspect vectoriel de l’objet représentant un état quantique (voir Axiomes de la mécanique quantique). Le nom provient d'un jeu de mots avec le terme bracket qui signifie " crochet de parenthèse ", en l'occurrence " \ \langle\ " et " \ \rangle\ " respectivement appelés " bra " et " ket ". Cette notation est depuis reprise dans l’étude mathématique de l’algèbre des opérateurs, et dont le champ d’application est plus large.

Le 'ket'

Définition

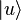
Soit un vecteur de l’espace des états. Il est noté \left| u \right\rangle et s'appelle vecteur-ket ou ket.

Deux kets forment un espace vectoriel linéaire. Ainsi, si λ1 et λ2 sont des nombres complexes quelconques,

\left| v \right\rangle = \lambda_1 \cdot \left| u_1 \right\rangle + \lambda_2 \cdot \left| u_2 \right\rangle

est un ket.

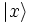
En allant plus loin, si \ |x\rangle\ dépend d’un indice continu \ x\ , et si \ f\ est une fonction complexe, alors,

\left| u \right\rangle = \int_{x_1}^{x_2}{f(x) \cdot d{x}}

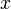
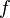
est un ket.

Propriétés

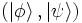
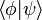
Le produit scalaire de deux kets est un complexe, noté \left( \left| \phi \right\rangle, \left| \psi \right\rangle \right) ou plus simplement \left\langle \phi | \psi \right\rangle (voir plus bas : bra). Ce produit est antilinéaire, c’est-à-dire que :

\left\langle \phi | \lambda \cdot \psi_1 + \mu \cdot \psi_2 \right\rangle = \lambda \cdot \left\langle \phi | \psi_1 \right\rangle + \mu \cdot \left\langle \phi | \psi_2 \right\rangle

mais que :

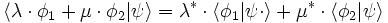
\left\langle \lambda \cdot \phi_1 + \mu \cdot \phi_2 | \psi \right\rangle = \lambda^* \cdot \left\langle \phi_1 | \psi \cdot \right\rangle + \mu^* \cdot \left\langle \phi_2 | \psi \right\rangle .

(l'expression \ c^*\ signifie que l'on prend le complexe conjugué de \ c\ — voir les nombres complexes)

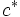
Ce choix permet la définition d’une norme, qui est positive dans l’espace scalaire des nombres complexes. En effet, le produit scalaire d’un vecteur par lui-même est égal au carré de sa norme :

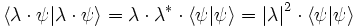
\left\langle \lambda \cdot \psi | \lambda \cdot \psi \right\rangle = \lambda \cdot \lambda^* \cdot \left\langle \psi | \psi \right\rangle = {\left|\lambda\right|}^2 \cdot \left\langle \psi | \psi \right\rangle ,

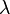
avec \ \lambda\ un scalaire une sorte de facteur d’échelle. Et d'où :

\left\langle \psi | \psi \right\rangle = {\left|\left| \psi \right|\right|}^2

Base & composantes

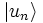
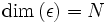
Il est commode d’utiliser une base afin de définir les composantes d’un ket. Il s’agit d'un ensemble de vecteurs \left| u_n \right\rangle , linéairement indépendants. Il y a autant de vecteurs que de dimensions dans l’espace des états \ \epsilon\ , et \dim{\left( \epsilon \right)} = N .

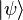
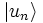
Ainsi, on peut décomposer \left| \psi \right\rangle dans la base des \left| u_n \right\rangle  :

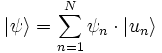
\left| \psi \right\rangle = \sum_{n = 1}^N {\psi_n \cdot \left| u_n \right\rangle} ,

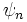
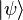
où \ \psi_n\ sont les composantes de \left| \psi \right\rangle et appartiennent aux nombres complexes.

On représente généralement un ket comme un vecteur colonne, une suite de nombres (les composantes) rangés verticalement :

\left| \psi \right\rangle = \begin{pmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{pmatrix}_{\epsilon} = \begin{bmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{bmatrix} \cdot \begin{bmatrix} \left| u_1 \right\rangle & \left| u_2 \right\rangle & \cdots & \left| u_N \right\rangle \end{bmatrix}

Le 'bra'

Définition

On veut associer à chaque ket d’un espace \ \epsilon\ , un nombre complexe. On définit pour cela une fonctionnelle linéaire \ \chi\ telle que :

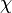
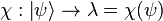
\chi : \left| \psi \right\rangle \rightarrow \lambda = \chi(\psi) , et
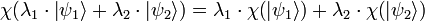
\chi{\left( \lambda_1 \cdot \left| \psi_1 \right\rangle + \lambda_2 \cdot \left| \psi_2 \right\rangle \right)} = \lambda_1 \cdot \chi{\left( \left| \psi_1 \right\rangle \right)} + \lambda_2 \cdot \chi{\left( \left| \psi_2 \right\rangle \right)}

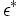
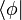
L’ensemble de ces fonctionnelles linéaires constitue un espace vectoriel \ \epsilon^*\ , dit espace dual de \ \epsilon\ . On appelle vecteur-bra ou bra un élément de cet ensemble et on le note \left\langle \phi \right| .

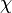
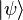
Ainsi, quand la fonctionnelle linéaire \ \chi\ agit sur \left| \psi \right\rangle , on obtient :

\chi{\left( \left| \psi \right\rangle \right)} = \lambda = \left\langle \phi | \psi \right\rangle

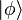
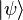
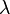
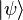
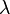
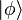
Cette nouvelle notation souligne en fait la relation qu’il existe entre bra, ket et le produit scalaire entre kets. Prenons un ket \left| \phi \right\rangle . Son produit scalaire avec \left| \psi \right\rangle donne un nombre \ \lambda\ . On a ainsi défini une fonctionnelle linéaire qui à \left| \psi \right\rangle fait correspondre un nombre complexe \ \lambda\ , à partir de \left| \phi \right\rangle  :

\phi{(|\psi\rangle)} = \lambda = \left( \left| \phi \right\rangle, \left| \psi \right\rangle \right)

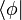
Puisque cette fonctionnelle se note \left\langle \phi \right| , on écrit également :

\left( \left| \phi \right\rangle, \left| \psi \right\rangle \right) = \left\langle \phi \right| \cdot \left| \psi \right\rangle = \left\langle \phi | \psi \right\rangle

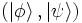
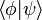
Ceci nous amène à dire qu’à chaque ket, correspond un bra, tel que le produit scalaire \left( \left| \phi \right\rangle, \left| \psi \right\rangle \right) s’écrive \left\langle \phi | \psi \right\rangle . Cette correspondance n’est cependant absolument pas réciproque. Il existe des bras (non linéaires) qui n’ont aucun " équivalent ket " (ces bras sont des fonctionnelles non linéaires pour lesquels il n’existe pas de ket unique respectant l’égalité, soit parce que l’équation n'a pas de ket solution, soit parce qu’il existe plusieurs kets solutions de l’équation).

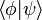
L’écriture \left\langle \phi | \psi \right\rangle revêt alors deux significations, l’une étant le résultat de l’application d’une fonctionnelle à un ket, l’autre étant le produit scalaire de deux kets.

Propriétés

Il existe une correspondance entre bra et ket :

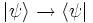
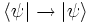
\left| \psi \right\rangle \rightarrow \left\langle \psi \right| (mais \left\langle \psi \right| \rightarrow \left| \psi \right\rangle n’est pas toujours vrai.)

L’antilinéarité du produit scalaire implique la correspondance suivante :

\lambda \cdot \left| \psi \right\rangle \rightarrow \lambda^* \cdot \left\langle \psi \right|

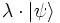
En effet, la norme de \lambda \cdot \left| \psi \right\rangle est définie positive :

{\left|\left| \lambda \cdot \left| \psi \right\rangle \right|\right|}^2 = \lambda \cdot \lambda^* \cdot \left\langle \psi | \psi \right\rangle = \left( \lambda^* \cdot \left\langle \psi \right| \right) \cdot \left( \lambda \cdot \left| \psi \right\rangle \right)

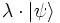
On identifie le ket \lambda \cdot \left| \psi \right\rangle , ce qui implique que le " reste " de l’expression est le correspondant dans l’espace dual des fonctionnelles linéaires.

Composantes

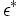
L’écriture de la norme permet d’écrire un bra sous forme de composantes dans l’espace vectoriel dual \ \epsilon^*\ de même dimension que l’espace vectoriel \ \epsilon\ des états :

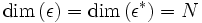
\dim{\left( \epsilon \right)} = \dim{\left( \epsilon^* \right)} = N ,
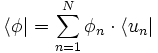
\left\langle \phi \right| = \sum_{n = 1}^N{\phi_n \cdot \left\langle u_n \right|} ,
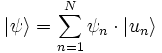
\left| \psi \right\rangle = \sum_{n = 1}^N{\psi_n \cdot \left| u_n \right\rangle} .

On représente aussi le bra sous la forme d’un vecteur ligne, une suite de nombres (les composantes) rangés horizontalement :

\left\langle \phi \right| = \begin{pmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_N \end{pmatrix}_{\epsilon^*} = \begin{bmatrix} \phi_1 & \phi_2 & \cdots & \phi_N \end{bmatrix} \cdot \begin{bmatrix} \left\langle u_1 \right| \\ \left\langle u_2 \right| \\ \vdots \\ \left\langle u_N \right| \end{bmatrix}

On notera que le produit matriciel ci-dessus est commutatif car la matrice ligne ne contient que des scalaires, la matrice colonne que des bras unitaires, et le produit d’un scalaire et d’un bra est commutatif, et car le produit matriciel d’une matrice colonne et d’une matrice ligne, s'il est défini, est toujours commutatif. Il en est de même du produit matriciel d’une matrice colonne de scalaires et d’une matrice ligne de kets.

Il est alors possible d’écrire le produit scalaire d'un bra et d’un ket sous forme du produit de quatre matrices : deux matrices scalaires et des matrices de bras unitaires ou de kets unitaires. En permutant les matrices scalaires, il reste à déterminer le produit de matrices de bras unitaires et de kets unitaires. Or on note que ces matrices unitaires sont transposées et conjuguées, ce qui signifie que leur produit se réduit au produit de leurs normes. Comme par définition, la norme des matrices unitaires est 1, ces matrices unitaires peuvent être éliminées du produit scalaire. La définition même du produit scalaire nous permet alors de l'écrire simplement en terme de produit de deux matrices scalaires de la façon suivante :

\left\langle \phi | \psi \right\rangle = \left( \begin{pmatrix} \phi_1 \\ \phi_2 \\ \vdots \\ \phi_N \end{pmatrix}_{\epsilon^*}, \begin{pmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{pmatrix}_{\epsilon} \right) = \begin{bmatrix} \phi_1 & \phi_2 & \cdots & \phi_N \end{bmatrix} \cdot \begin{bmatrix} \psi_1 \\ \psi_2 \\ \vdots \\ \psi_N \end{bmatrix} = \sum_{n = 1}^N{\phi_n \cdot \psi_n}

Etymologie

En anglais bracket signifie " crochet ", ce qui a donné leur nom aux bra-ket, un peu comme " babord " et " tribord ".

Opérateurs et notation de Dirac

D’une façon générale les opérateurs linéaires agissant sur l’espace \ \epsilon\ des états peuvent s’écrire sous la forme d’une combinaison linéaire d'opérateurs de la forme suivante :

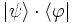
\left| \psi \right\rangle \cdot \left\langle \varphi \right| ,

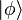
dont l’action sur un état, représenté par le ket \left| \phi \right\rangle , sera tout simplement l’état :

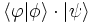
\left\langle \varphi | \phi \right\rangle \cdot \left| \psi \right\rangle ,

permettant une grande économie d’écriture.

miniature
Voici ce qui a causé les toutes premières inégalités de richesse 💰
miniature
Quelle est cette zone étrange dans l'Atlantique Nord ? 🌊
miniature
Cette planète orbite à angle droit autour de deux étoiles, une première ! 🔭
miniature
Des cellules solaires flexibles battent des records d'efficacité ⚡
miniature
Ce dispositif reproduit les trous noirs et trous blancs en laboratoire 🌀
miniature
Record établi pour un transistor en diamant 💎
miniature
Les sursauts radio rapides trahissent enfin leur origine cosmique 📡
miniature
Ces biomarqueurs sanguins prédisent la démence 10 ans à l'avance 🧠
miniature
Découverte majeure: des médicaments 23 fois plus efficaces contre le cancer 💊
miniature
Les oscillations collectives des foules humaines denses 🔁
miniature
Une forme inconnue de la matière détectée au LHC ? ⚛️
miniature
Le sel, un facteur méconnu de l'obésité ? 🧂
miniature
L'Univers en rotation, une réponse élégante à ce problème astrophysique majeur 🌀
miniature
Découverte tectonique majeure sous les Petites Antilles 🌍
miniature
1
Peut-on geler en chauffant ? ❄️
miniature
Une peau électronique pour doter les robots du sens du toucher 👌
miniature
Invention d'un bois semi-transparent avec une technique...surprenante ! 🌳
miniature
Le cancer inscrit dans nos gènes dès la naissance ? 🧬
miniature
Des supernovae à l'origine de deux extinctions massives sur Terre ? 💥
miniature
Le passé verdoyant du plus grand désert du monde 🐪
miniature
Après les campagnes antivaccins, la rougeole revient en force aux États-Unis 😷
miniature
Des puces quantiques plus proches que jamais ⚡
miniature
1
Pourrons-nous bientôt communiquer avec les dauphins grâce à l'IA ? 🐬
miniature
En déplaçant deux atomes, des chercheurs transforment le LSD en médicament surpuissant 💊
miniature
Des scientifiques parviennent à produire efficacement du carburant à partir de monoxyde de carbone 🛢️
miniature
Que nous apprend la découverte de cet insecte de 16 millions d'années ? 🐜
miniature
Avec 91km, l'accélérateur FCC fera passer le LHC pour un jouet ⚛️
miniature
Cette vitamine développe les fonctions cognitives du cerveau 🧠
miniature
Comment des impacts géants vaporisent les corps planétaires ☄️
miniature
Les Américains riches vivent moins longtemps que les Européens pauvres 💰
miniature
Attention à ce riz naturellement riche en arsenic 🍚
miniature
L'intelligence artificielle contre la mort subite 💀
miniature
L'inévitable formation d'un océan de magma basal sur Terre 🔥
miniature
Découverte d'une plante étrange sans chlorophylle 🌱
miniature
Existe-t-il des mélodies naturelles ? 🎶
miniature
Cette exoplanète présente une signature de vie bien plus forte que celle de la Terre 👽
miniature
L'origine énigmatique des rayons cosmiques les plus énergétiques ⚡
miniature
1
Le diagnostic de l'autisme remis en cause par l'intelligence artificielle 🩺
miniature
Imprimer en 3D avec la lumière du soleil ☀️
miniature
La pollution atmosphérique nuit gravement au cerveau 🧠
miniature
Le trou noir supermassif Ansky vient de se réveiller ⚫
miniature
1
Voici ce qui rend notre cerveau vraiment unique 🧠
miniature
Asymétrie matière-antimatière: une nouvelle pièce du puzzle dévoilée 🧩
miniature
Neige en inuit, goût en japonais... comment les langues décomposent la réalité ? 💬
miniature
La physique révèle les secrets d'un strike parfait au bowling 🎳
miniature
Le TDAH associé à la démence 🧠
miniature
Découverte d'une nouvelle forme d'intrication quantique, une première en 20 ans ⚛️
miniature
Le régime cétogène montre des surprises sur le cholestérol 🧐
miniature
Un tango observationnel révèle une Super-Terre 🔭
miniature
Cette expérience montre que la graisse brune augmente fortement la longévité 🕒
Page générée en 0.136 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales
Version anglaise | Version allemande | Version espagnole | Version portugaise