Hypergraphe - Définition
Les hypergraphes sont des objets mathématiques généralisant la notion de graphes. Ils ont été nommés ainsi par Claude Berge en 1960.
Présentation générale
Les hypergraphes généralisent la notion de graphe dans le sens où les arêtes ne relient plus un ou deux sommets, mais un nombre quelconque de sommets (compris entre un et le nombre de sommets de l’hypergraphe). De nombreux théorèmes de la théorie des graphes se généralisent naturellement aux hypergraphes, par exemple le théorème de Ramsey.
Les hypergraphes ont des applications dans tous les domaines où on utilise la théorie des graphes : résolution de problèmes de satisfaction de contraintes, traitement d’images, optimisation d’architecture réseaux, modélisation, etc.
Définitions
Hypergraphe
Soient
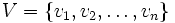
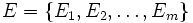
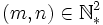
Un hypergraphe H est un couple (V,E) tel que :
-
![\forall i \in ([1,m]\cap\N) \quad {E_i \neq \varnothing}](https://static.techno-science.net/illustration/Definitions/autres/a/ae7f4162645d41d69e405140afedb57c_edf3c9f81465bf2f8dbd96e72103ba4c.png)
-
![\forall i \in ([1,m]\cap\N) \quad {E_i \neq \varnothing}](https://static.techno-science.net/illustrationWebp/Definitions/autres/a/ae7f4162645d41d69e405140afedb57c_edf3c9f81465bf2f8dbd96e72103ba4c.png)
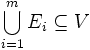
A l'instar des graphes, on dit que :
- Les éléments de V sont les sommets de H.
- Le nombre de sommets n est l'ordre de l'hypergraphe.
- Les éléments de E sont les arêtes de H.
un hypergraphe c'est juste une matrice 0-1! mais attention certains mettent les arêtes en ligne (c'est mon cas) et d'autres en colonne... un hypergrahe est autodual si sa matrice est symétrique. le top du top c'est quand un autodual est autotransversal.
Hypergraphe uniforme
Parmi les propriétés "nouvelles" — au sens : non définies avec les graphes — introduites avec les hypergraphes figurent deux notions associées.
- On appelle rang d'un hypergraphe le nombre maximum de sommets d'une arête :
-
![\operatorname{rang}(H) = \max_{i \in [1,m]\cap\N} |E_i|](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d156037ca2fa88cc2bac0d459db48bbc_890c02599266c21cb0661639eb6be9de.png)
- Le rang d'un hypergraphe est majoré par son ordre. Si rang(H) = 2, alors H est un multigraphe.
- On appelle anti-rang d'un hypergraphe le nombre minimum de sommets d'une arête :
-
![\operatorname{anti-rang}(H) = \min_{i \in [1,m]\cap\N} |E_i|](https://static.techno-science.net/illustrationWebp/Definitions/autres/d/d5cd1c2e73ca52292bc160e7e58a0c0b_d620d5e257cc3d418a46501f3cadd3fb.png)
Par définition d'un hypergraphe, les arêtes sont des parties non vides de l'ensemble des sommets de l'hypergraphe. L'anti-rang d'un hypergraphe est donc non nul.
Un hypergraphe est dit uniforme lorsque son rang et son anti-rang sont égaux.
On parle aussi d' hypergraphe r-uniforme pour désigner un hypergraphe uniforme de rang r.
Hypergraphe partiel et sous-hypergraphe
A l'instar des graphes, on dit que :
- Un hypergraphe partiel Hp = (V,Ep) d'un hypergraphe H = (V,E) est tel que :
-
-
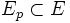
- Un sous-hypergraphe H' = (V',E') d'un hypergraphe H = (V,E) est tel que :
-
-
-
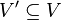
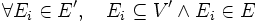
Ces notions généralisent à la théorie des hypergraphes les notions de graphe partiel et de sous-graphe.
Hypergraphe simple
A l'instar des graphes, on dit que :
- Un hypergraphe simple est un hypergraphe (V, E) tel que, pour toute paire d'arêtes {Ei,Ej} de E :
-
-
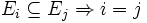
Dans le cas où toutes les arêtes de E sont de cardinalité égale à 2, H est un graphe simple non orienté au sens classique de la théorie des graphes.
on les appelle aussi "famille de Sperner" ou "anti-chaîne".
Hypergraphe dual
Soit
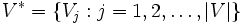
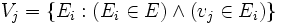
Alors l'hypergraphe défini par H * = (E,V * ) est appelé hypergraphe dual de H. beaucoup plus simplement il suffit de prendre la transposée de la matrice.
(12,13,23) est à la fois autodual et autotransversal.
un hypergraphe est "waou!" s'il possède plusieurs propriétés remarquables. ex: P = (123,145,167,246,257,347,356). P est un plan projectif, P est autotransversal, uniforme, régulier et autodual. qui dit mieux?
