Diagramme de Voronoï - Définition
En mathématiques, un diagramme de Voronoï (aussi appelé décomposition de Voronoï ou partition de Voronoï du nom du mathématicien russe Georgi Fedoseevich Voronoï (1868 - 1908)) est une décomposition particulière d’un espace métrique déterminée par les distances à un ensemble discret d’objets de l’espace, en général un ensemble discret de points.
Définition
On se place dans un espace euclidien E. soit S un ensemble fini de n points de E; les éléments de S sont appelés centres, sites ou encore germes.
On appelle région de Voronoï ou cellule de Voronoï associée à un élément p de S l’ensemble des points qui sont plus proches de p que de tout autre point de S.
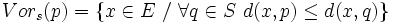
Pour deux point a et b de S, l’ensemble Π(a,b) des points équidistant de a et b est un hyperplan affine (un sous-espace affine de co-dimension 1). Cet hyperplan est la frontière entre l’ensemble des points plus proche de a que de b, et l’ensemble des points plus proches de b que de a.
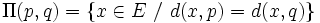
On note H(a,b) le demi espace délimité par cet hyperplan contenant a, il contient alors tout les points plus proches de a que de b. La région de Voronoï associée à a est alors l’intersection des H(a,b) où b parcourt S\{a}.
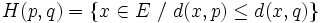
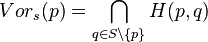
Les régions de Voronoï sont des polytopes convexes en tant qu’intersection de demi espaces. L’ensemble de tels polygones partitionne E, et est la partition de Voronoï correspondant à l’ensemble S.
En dimension 2 il est facile de tracer ces partitions, on les appelle dans ce cas parfois diagrammes de Voronoi. On se base sur le fait que la frontière entre les cellules de Voronoi de deux germes distincts se situe forcément sur la médiatrice qui sépare ces deux germes. En effet, les points de cette médiatrice sont équidistants des deux germes donc on ne peut pas affirmer qu'il se situent dans l'une ou l'autre cellule de Voronoi. Pour un ensemble de germes, le diagramme de Voronoi se construit donc en déterminant les médiatrices de chaque couple de germes. Un point d'une médiatrice appartient alors à une frontière de Voronoi s'il est équidistant d'au moins deux germes et qu'il n'existe pas de distance plus faible entre ce point et un autre germe de l'ensemble.
Le diagramme de Voronoï est le dual de la triangulation de Delaunay, on peut définir la triangulation de Delaunay à partir du diagramme de Voronoï, deux points p et q créent une arête dans le graphe de Delaunay si et seulement si les régions de Voronoï associées à p et q sont adjacentes.
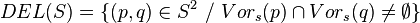
Histoire
L’usage informel des diagrammes de Voronoï remonte à Descartes en 1644. Dirichlet a utilisé des diagrammes de Voronoï en dimension 2 ou 3 dans son étude des formes quadratiques en 1850.
Le physicien britannique John Snow a utilisé un diagramme de Voronoï en 1854 pour montrer que la majorité des personnes mortes dans l’épidémie de choléra de Soho vivait plus près de la pompe infectée de Broad Street que de n’importe quelle autre pompe.
Les diagrammes de Voronoï portent le nom du mathématicien russe Georgy Fedoseevich Voronoï (ou Voronoy) qui a défini et étudié le cas général en dimension n en 1908. Les diagrammes de Voronoi qui sont utilisés en géophysique et en météorologie pour analyser des données de distributions spatiales (comme les mesures de chutes de pluie) sont appelés polygones de Thiessen du nom du météorologiste américain Alfred H. Thiessen.
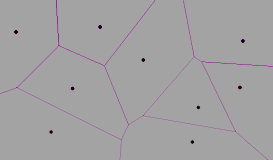
Exemple
L'exemple suivant reprend les mêmes points que l'exemple de la triangulation de Delaunay :
Algorithmes
L'algorithme de Steven Fortune (1987, Laboratoires Bell AT&T), démontré comme optimal, permet de calculer le diagramme de Voronoï d'un ensemble de n points dans le temps O(nlog(n)).
Applications
Les diagrammes de Voronoï sont utilisés, ou réinventés sous de nombreux noms, dans différents domaines. Ils interviennent souvent lorsque l'on cherche à partitionner l'espace en sphères d'influence :
- Reconstruction de données géographiques optimales, pour un simulateur de vol par exemple.
- Effet de Mosaïque dans un logiciel de retouche d'image.
- Construction d'un dôme géodésique dual
- Partition des structures spatiales des populations d'étoiles.
- Diagnostic de cellules cancéreuses.
- Modélisation de microstructures telles que certains aciers.
- Simulation de la circulation des fluides dans les milieux poreux.
- Calculs de trajectoire en robotique mobile.
- ...


















































