Coloration de graphe - Définition

Le problème de la coloration de graphe est en fait à l'origine de la théorie des graphes elle-même, puisque cette théorie est motivée, à l'origine, par le regroupement de diverses questions (et réponses) portant sur des structures combinatoires proches les unes des autres. Ainsi le problème des quatre couleurs (voir Théorème des quatre couleurs) consistait à trancher la question suivante : peut-on colorer chacune des faces d'un polyèdre (de l'espace usuel) sans que deux faces adjacentes aient la même couleur en n'utilisant que quatre couleurs au maximum ? Ce problème dépend uniquement de la structure combinatoire de graphe planaire que l'on peut associer naturellement à tout polyèdre (les faces correspondent aux sommets et l'adjacence entre faces à l'adjacence entre sommets). L'extension du problème aux graphes quelconques (pas nécessairement planaires) a trouvé sa motivation théorique principale avec la conjecture de Berge (récemment résolue, voir Théorème des graphes parfaits), et une motivation liée à diverses applications concrètes (notamment dans l'affection de fréquence).

Donnons maintenant une définition du problème.

Définition

La notion de coloration n'est définie que pour les graphes sans boucle, et la multiplicité des arêtes ne joue aucun rôle. Donc, soit G un graphe simple (sans boucle ni arête multiple), un stable de G est un sous-ensemble de sommets deux-à-deux non-adjacent, et une coloration de G est une partition de son ensemble de sommets en stables.

Notons que la définition originale de la coloration est la suivante^[1] : une coloration de G est une fonction associant à tout sommet de G une couleur (généralement un élément de l'ensemble d'indices des couleurs {1,2,...,n} où n est le nombre de sommets du graphe) telle que deux sommets adjacents n'ont pas la même couleur. On lui préfère généralement la définition que nous avons donné en premier, car, pour la plupart des questions liées au concept de coloration, on ne souhaite pas différencier les colorations qui ne sont distinctes que à permutation des indices de couleurs près ^[2]. C'est le cas pour le problème central lié à la coloration, celui de déterminer le nombre chromatique d'un graphe: le nombre chromatique de G est le nombre minimum de couleur dans une coloration de G. Dans ses différents ouvrages (en français ou en anglais), Claude Berge a utilisé les deux notations γ(G) et χ(G) pour désigner le nombre chromatique de G. De nos jour, la plupart des ouvrages adoptent le symbole χ(G) pour désigner le nombre chromatique de G (γ(G) concerne généralement un invariant lié au concept de cycle).

Aspects algorithmiques généraux

Déterminer le nombre chromatique d'un graphe est un problème NP-Complet dans le cas général. En fait, on peut en dire plus si l'on considère le problème de décision suivant: Soit G un graphe et k un entier, peut-on colorer G avec moins de k couleurs ?

Si k=2 il s'agit de décider si G est biparti ou non. Ceci est facile car ces graphes sont caractérisés par la non présence d'un structure interdite: celle de cycle impair. Par-contre pour tout k fixé supérieur à 3 le problème devient NP-Complet.

Ainsi, à moins que P=NP, il n'existe pas d'algorithme polynomial déterminant le nombre chromatique d'un graphe arbitraire. Pour certaines classes de graphes par-contre de tels algorithmes existent. C'est notamment le cas pour les graphes triangulés (ou chordaux) dans lequel le problème se résoud en temps linéaire. Un résultat nettement plus difficile (de László Lovász et al.) établit (en développant toute une théorie) que l'on peut déterminer en temps polynomial le nombre chromatique de tout graphe parfait (pour une définition voir Théorème des graphes parfaits).

Parmi les algorithmes exactes (donc de complexité exponentielle dans le cas général) citons l'algorithme de Zykov (par la méthode de Branch and Bound). L'importance du problème a donné lieu à l'élaboration de nombreuses heuristiques spécifiques au problème, spécialement des algorithmes séquentiels de coloration sommet par sommet (dsatur, cosine, maya, etc.). Elle a aussi sucité de nombreuses expérimentations des méthodes approchées générales: méta-heuristique (recuit simulé, tabou search), ou encore algorithme génétique...

Donnons quelques exemples des méthodes approchées spécifiques au problème de la coloration.

Algorithme de Welsh et Powell

Voici un exemple qui, en plus, fournit une preuve constructive du fait suivant: , où Δ(G) représente le degré maximum d'un sommet de G (le degré d'un sommet étant le nombre des arêtes qui lui sont incidentes). Pour s'en convaincre, appliquons l'algorithme suivant (Welsh et Powell):

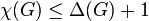
1. Repérer le degré de chaque sommet.
2. Ranger les sommets par ordre de degrés décroissants. (dans certains cas plusieurs possibilités)
3. Attribuer au premier sommet (A) de la liste une couleur.
4. Suivre la liste en attribuant la même couleur au premier sommet (B) qui ne soit pas adjacent à (A).
5. Suivre (si possible) la liste jusqu'au prochain sommet (C) qui ne soit adjacent ni à A ni à B.
6. Continuer jusqu'à ce que la liste soit finie.
7. Prendre une deuxième couleur pour le premier sommet (D) non encore colorié de la liste.
8. Répéter les opérations 4 à 6.
9. Continuer jusqu'à avoir coloré tous les sommets.

Remarquons que cette méthode peut aboutir à la pire des colorations possibles, par-exemple si le graphe G a la structure d'étoile (chacune des arêtes de G est incidente à un même sommet particulier) son nombre chromatique est 2 (si G a au-moins une arête) tandis que Welsh-Powell donne une coloration utilisant autant de couleur que de sommets ! L'heuristique DSATUR permet d'éviter ce problème.

DSATUR

On considère un graphe G=(V,E) simple connexe et non-orienté. Pour chaque sommet v de V, on calcule le degré de saturation DSAT(v) de la manière suivante:

Si aucun voisin de v n'est coloré alors
DSAT(v)=degré(v)
sinon
DSAT(v)= le nombre de couleurs différentes utilisées dans le premier voisinage de v

L'algorithme DSATUR est un algorithme de coloration séquentiel, au sens ou il colorie un seul sommet à la fois et tel que:

au départ le graphe n'est pas coloré
on colorie un sommet non-déjà coloré
on stoppe DSATUR quand tous les sommets de G sont colorés.

Dans un premier temps on voit bien d'une part que la preuve de terminaison est triviale et d'autre part que l'algorithme est séquentiel. Dans le détail l'algorithme est le suivant:

1. Ordonner les sommets par ordre décroissant de degré.
2. Colorer un sommet de degré maximum avec la couleur 1.
3. Choisir un sommet non coloré avec DSAT maximum. Si conflit choisir celui avec degré maximum.
4. Colorer ce sommet par la plus petite couleur possible
5. Si tous les sommets sont colorés alors stop. Sinon aller en 3.

Implémentations des heuristiques présentées

Deux versions de l'algorithme DSATUR sont accessibles:

• en C sur : http://prolland.free.fr/Cours/Cycle2/Maitrise/GraphsTheory/TP/PrgGraphDsat/dsat.html
• en Php sur : http://prolland.free.fr/works/research/dsatphp/dsat.html

A titre illustratif, voici une implémentation (partielle) de Welsh-Powell en Fortran 95:

!----------------------!
!                      !
! Algo de Welsh Powell !
!______________________!
function WP(M,nu_heuristique) result(RES)
logical, dimension(:,:), intent(in) :: M
integer, intent(in):: nu_heuristique
TYPE(VOISIN), dimension(:), pointer:: TMP,TMP1,TMP2
integer, dimension(:),pointer:: RES
integer:: h,i,j,color,last_color
i=0 ! nbre de sommets colorés
j=1 ! indice du prochain sommet à traiter
color=1 ! couleur du prochain sommet à colorer
allocate(RES(0:size(M,1)))
! DETERMINATION DE L'HEURISTIQUE A UTILISER:
if (nu_heuristique==0) then
! version brute
call CONV_VOISINS(M,TMP)
else
! version plus fine:
call CONV_VOISINS_TRIE(M,TMP)
end if
RES=0
! tant que tous les sommets ne sont pas marqué
do while(j<=size(M,1))
! si le sommet courant n'est pas marqué
if (RES(TMP(j)%NUM)==0) then
RES(TMP(j)%NUM)=color ! on colorie le sommet
i=i+1
last_color=color
! on cherche les non voisins de j dans l'ensemble de la matrice
call POINTS_NON_VOISINS(TMP,TMP(j)%NUM,TMP1)
! tant qu'il reste des non voisins
h=1
do while(h<=size(TMP1,1))
if (RES(TMP1(h)%NUM)==0) then
RES(TMP1(h)%NUM)=color
i=i+1
! et on déduit le sous ensemble n'étant ni voisin de j et des sommets déjà marqué
call POINTS_NON_VOISINS(TMP1,TMP1(h)%NUM,TMP2)
if (size(TMP2)==0) exit
call COPIE(TMP2,TMP1)
h=0
end if
h=h+1
end do
j=j+1 ! on passe au sommet suivant
color=color+1 ! ainsi qu'à la couleur suivante
else
j=j+1 ! sinon on passe au sommet suivant
end if
end do
RES(0)=last_color
end function WP