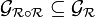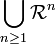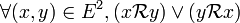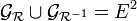Relation binaire - Définition
Une relation binaire est un concept mathématique qui systématise des notions comme " ... est supérieur ou égal à ... " en arithmétique, ou " ... est élément de l’ensemble ... " en théorie des ensembles. C’est un cas particulier de relation générale ou correspondance. On retrouve aussi ce concept en théorie des graphes.
Introduction
De manière informelle, une relation entre deux ensembles est une proposition qui lie certains éléments du premier ensemble avec d’autres éléments du second ensemble.
Sur un ensemble F constitué de filles et un ensemble G constitué de garçons, par exemple, on pourrait définir une relation " Alice aime Bernard ", ou une autre relation " Béatrice connaît Paul "... On peut donc voir la relation comme étant des fils reliant des éléments de deux ensembles.
Dans le cas d’un ensemble fini, on peut alors tenter de représenter la relation par un diagramme: si F = {Lucie, Béatrice, Delphine, Alice} et si G = {Bernard, Antoine, Paul, Charles}, la relation aime peut être schématisée par le diagramme suivant :
On pourra déplorer le fait que Delphine n’aime personne, que Lucie ait un cœur généreux et que Charles puisse se sentir seul.
On peut aussi tenter de faire la liste des couples ainsi en relation. (pour plus de commodité, on ne conservera que les deux premières lettres du prénom)
- Gr = {(Lu,Be) , (Lu, An) , (Lu, Pa) , (Bé, An) , (Al, Pa) , (Al, Be)}
En mathématique, un " couple " est formé de deux éléments mis entre parenthèses dans un ordre particulier. La relation est définie en première approche comme un ensemble de couples, c’est-à-dire que si deux éléments sont reliés entre eux, alors le couple est un élément de l’ensemble relation. Si l’on appelle F l’ensemble des filles, et G l’ensemble des garçons, alors l’ensemble de tous les couples possibles est appelé " produit cartésien de F par G " et est noté F×G et la relation aime est alors définie par l’ensemble F, l’ensemble G et un sous-ensemble de F×G.
Définition formelle
Une relation binaire

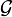
Si
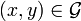
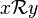
- Dans le cas particulier où E = F on dit que

- Dans le cas où E = F×F, on parlera de relation ternaire interne sur F.
- Plus généralement, si E = F n - 1, on parlera de relation n-aire sur F.
On remarquera qu’il est nécessaire, dans une relation binaire, de préciser l’ensemble E (appelé ensemble de départ), l’ensemble F (appelé ensemble d’arrivée) ET la partie
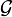
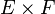
Une relation binaire peut être considérée comme une fonction de E×F à valeur dans l’ensemble { Vrai , Faux } , et qui à un couple ( x , y ) associe Vrai si x est en relation avec y et Faux sinon (indiquant si le couple ( x , y ) est un élément du graphe de la relation ou non).
Composition et inversion
Composition
Si

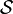
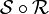
Notation: si

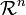

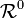
Inversion
Si

-
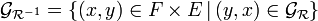
Exemples:
- " plus petit que " et " plus grand que " sont des relations inverses l’une de l’autre.
- " aime " et " est aimé par " sont aussi inverses l’une de l’autre.
Relation fonctionnelle
Lorsque, pour tout élément x de E, x n’est en relation qu’avec 0 ou 1 élément y de F, on dit que la relation est fonctionnelle. C’est un cas particulier de fonction. En langage formel, la propriété précédente s’écrit :
Pour plus de précisions, voir l'article " Fonction mathématique ".
Exemple important :
- La diagonale de E est définie par :
-
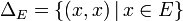
-
- C’est le graphe de la relation d’égalité sur E, notée " =E ", ou " = " en l’absence d’ambiguïté sur l’ensemble concerné.
- Cette relation est aussi une fonction, l’identité de E, notée " IdE ".
Relation sur (ou dans) un ensemble
Si E = F, on parlera de relation sur (ou dans) E.
Propriétés liées à la réflexivité
Relation réflexive
La relation

Une relation est donc réflexive ssi son graphe contient la diagonale de E, c’est-à-dire si :
En d’autres termes, l’intersection du graphe de la relation avec la diagonale de E est égale à cette diagonale.
Exemples:
- la relation d’inclusion entre ensembles est réflexive : tout ensemble est inclus dans lui-même;
- dans un ensemble de nombres, la relation " est un diviseur de " est réflexive : tout nombre est son propre diviseur;
- dans un ensemble de personnes, la relation " est de la même famille que " est réflexive...
La clôture réflexive, notée "
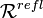


Relation irréflexive
La relation

Une relation est donc irréflexive ssi son graphe est disjoint de la diagonale de E, c’est-à-dire si :
L’intersection du graphe de la relation avec la diagonale de E se réduit donc à l’ensemble vide.
Exemples :
- l’inégalité stricte sur les entiers est un exemple de relation irréflexive : aucun entier n’est strictement inférieur à lui-même;
- dans un ensemble de personnes, la relation " est enfant de " est irréflexive : personne n’est son propre enfant;
- dans un polyèdre, la relation " a un et un seul côté commun avec " est une relation irréflexive entre ses faces : aucune face n’a qu’un seul côté commun avec elle-même...
Une relation sur un ensemble d'au moins deux éléments peut bien entendu n'être ni réflexive, ni irréflexive, il suffit qu'un élément soit en relation avec lui même et l'autre non.
Les seules relations à la fois réflexives et irréflexives sont les relations dont le graphe est vide.
Propriétés liées à la symétrie
Relation symétrique
La relation

Une relation est donc symétrique ssi son graphe se confond avec celui de sa relation inverse, c’est-à-dire si :
ou encore :
-
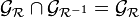
Exemples :
- dans un ensemble de personnes, la relation " est de la même famille que " est symétrique;
- dans un polyèdre, la relation " a un et un seul côté commun avec " est une relation symétrique entre ses faces : si une face a un côté commun avec une autre face, cette dernière a le même côté commun avec la première face;
- parmi les entiers naturels, la relation " forme un produit pair avec " est symétrique, car la multiplication des entiers est commutative.
La clôture symétrique, notée "
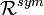


Cette clôture symétrique est d’ailleurs universelle parmi les relations symétriques contenant

Relation antisymétrique
La relation

Une relation est donc faiblement antisymétrique ssi l'intersection de son graphe avec celui de sa réciproque est incluse dans la diagonale de E, c'est-à-dire si :
-
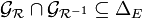
Exemples:
- les relations " plus grand que " et " plus petit que " sur les entiers naturels ou sur les réels.
- la relation " divise " dans l’ensemble des entiers naturels
Quand une relation est à la fois anti-symétrique et irréflexive, on dit parfois qu'elle est fortement antisymétrique. On peut alors simplifier la définition.
La relation

Une relation est donc fortement antisymétrique ssi l’intersection de son graphe avec celui de sa réciproque est vide, c’est-à-dire si :
-
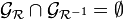
Exemples :
- les relations d'ordre strict, comme la relation " est strictement plus grand que " sur les entiers ou les réels, ou la relation d'inclusion stricte sont fortement antisymétriques.
- dans un ensemble de personnes, la relation " est enfant de " est asymétrique : personne n’est son propre enfant, ni a fortiori l’enfant de ses enfants...
Pour une relation dont on sait par ailleurs qu'elle est irréflexive, l'antisymétrie forte et l'antisymétrie sont équivalentes, et donc la plupart du temps onparle simplement d'antisymétrie.
Les seules relations symétriques et fortement antisymétriques sont les relations vides. Par contre l'égalité sur n'importe quel ensemble est une relation à la fois symétrique et antisymétrique.
Une relation peut n'être ni symétrique ni antisymétrique, comme par exemple la relation de divisibilité sur les entiers relatifs.
Transitivité
La relation

Une relation

Exemple :
- la relation
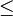
On appelle clôture transitive de

elle est universelle parmi les relations transitives contenant

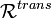
Relation totale
La relation

La relation est donc totale ssi l'union de son graphe avec celui de sa réciproque est égale au carré cartésien de E, c'est-à-dire si :
Exemple : la relation
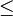
Contre-exemple : la relation " divise " sur l'ensemble des entiers naturels n'est pas totale.
Relation d'équivalence
Une relation d'équivalence est une relation réflexive, transitive et symétrique. L'exemple le plus simple de relation d'équivalence est l'égalité. En arithmétique la relation de congruence modulo un entier donné est une relation d'équivalence.
Pour plus d’information voir l’article " Relation d'équivalence ".
Relation d’ordre
Une relation d’ordre est une relation réflexive, transitive et antisymétrique.
Si la relation est totale alors on dit que l’ordre est total. C’est le cas de la relation " plus grand que " sur les entiers naturels. Tous les éléments ne sont pas forcément comparables par une relation d’ordre ; par exemple deux entiers naturels ne sont pas forcément comparables par divisibilité. On dit alors que la divisibilité est un ordre partiel sur N.
Plus de détails dans l’article " Relation d'ordre ".
Relation bien fondée
Voir relation bien fondée.
Exemples
- La relation d’appartenance sur
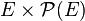
- La relation d’inclusion sur
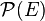
- La relation inférieur ou supérieur sur

- la relation divise sur

- La relation d’égalité (congruencielle ou non) sur E (relation d’équivalence)
Nombre de relations binaires sur des ensembles finis
Considérons un ensemble E fini de cardinal n et un ensemble F fini de cardinal p. Nous pouvons facilement démontrer qu’il y a autant de relations binaires de E sur F que d’applications de E×F dans { 0 , 1 } , ce qui donne 2 np relations.
En particulier, si E = F , on trouve
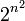
-
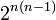
-
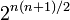
- Pour le nombre de relations transitives, il n’y a toujours pas actuellement de formule " fermée "
Le nombre de relations d’équivalence est égal au nombre de partitions d’un ensemble, c’est-à-dire le nombre de Bell.
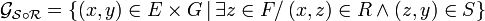
![\forall x \in E, \forall y \in F, \forall z \in F , [ ( x , y ) \in \mathcal{G}_{\mathcal{R}} \and ( x , z ) \in \mathcal{G}_{\mathcal{R}} ] \Rightarrow ( y = z ) \,](https://static.techno-science.net/illustration/Definitions/autres/7/7e9905b50dbaff1a1250f9a537252c93_119ab4f2efce304843ed6295ee3df635.png)
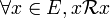
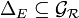
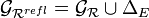
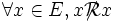
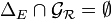
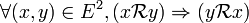
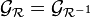
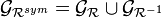
![\forall ( x , y ) \in E^2 , [ ( x \mathcal{R} y ) \wedge ( y \mathcal{R} x ) ] \Rightarrow ( x = y ) \,](https://static.techno-science.net/illustration/Definitions/autres/2/2d59314f4ca5d3e48a0fb855772fd825_da60aa894569708279cc13afe5a5c0e2.png)
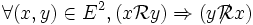
![\forall ( x , y , z ) \in E^3 , [ ( x \mathcal{R} y ) \wedge ( y \mathcal{R} z ) ] \Rightarrow ( x \mathcal{R} z ) \,](https://static.techno-science.net/illustration/Definitions/autres/b/bdf5aaaf8334a8f4e4589efac4c5e062_9e46d974698ef74f359157175832a433.png)