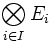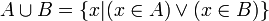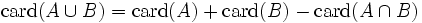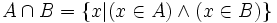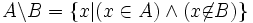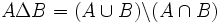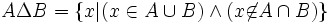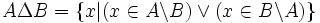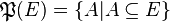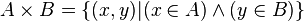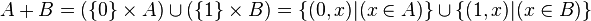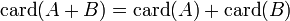Opération ensembliste - Définition

Les opérations ensemblistes sont les opérations mathématiques faites sur les ensembles, sans s’occuper de la nature des éléments qui composent ces ensembles.

Réunion

La réunion de deux ensembles A et B, notée (lire " A union B "), se définit par :

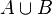
L’existence de l’ensemble résultant est garantie par l’axiome de la réunion. Son unicité découle de l’axiome d'extensionnalité.

Nous pouvons remarquer qu’il est possible d’établir un homomorphisme entre l’univers des ensembles muni de la réunion et celui des propositions muni du ou logique. La réunion est ainsi dans l’univers des ensembles une loi de composition interne associative, commutative, idempotente, unifère et distributive par rapport à l’intersection (voir ci-après). L’ensemble vide en est l’élément neutre.

La réunion est aussi une loi interne dans l’ensemble P(E) des parties d’un ensemble E quelconque. Elle y possède non seulement les mêmes propriétés que ci-dessus, mais est de surcroît absorbante et son élément absorbant est l’ensemble E entier. Par contre, elle n’est en général ni régulière, ni inversible.

Le cardinal de l’union de deux ensembles n’est pas en général la somme des cardinaux de ces deux ensembles (sauf s’ils sont disjoints, c’est-à-dire si leur intersection est vide) :

Intersection

L’intersection de deux ensembles A et B, notée (lire " A inter B "), se définit par :

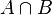
Nous pouvons remarquer qu’il est possible d’établir un homomorphisme entre l’univers des ensembles muni de l’intersection et celui des propositions muni du et logique. L’intersection est ainsi dans l’univers des ensembles une loi de composition interne associative, commutative, idempotente, absorbante et distributive par rapport à la réunion. L’ensemble vide en est l’élément absorbant.

L’intersection est aussi une loi interne dans l’ensemble P(E) des parties d’un ensemble E quelconque. Elle y possède non seulement les mêmes propriétés que ci-dessus, mais est de surcroît unifère et son élément neutre est l’ensemble E entier. Par contre, elle n’est en général ni régulière, ni inversible.

Complémentation ou différence

La complémentation d’un ensemble B dans un ensemble A, notée (lire " A moins B " ou " complément de B dans A "), se définit par :

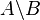
La complémentation est dans l’univers des ensembles une loi interne unifère à droite et absorbante à gauche d’élément neutre à droite et absorbant à gauche l’ensemble vide.

Différence symétrique ou réunion disjointe

La réunion disjointe de deux ensembles A et B, notée AΔB (lire " A delta B "), se définit par :

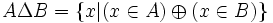
(rappel : désigne le ou exclusif logique)

Il existe d'autres définitions équivalentes :

Cette dernière définition justifie l’appellation de différence symétrique souvent donnée à cette opération.

La réunion disjointe est une loi interne de l’univers des ensembles, associative, commutative et unifère d’élément neutre l’ensemble vide.

Ensemble des parties

L’ensembles des parties d’un ensemble E, noté habituellement (E) ou (E), est, comme son nom l’indique, l’ensemble formé par tous les sous-ensembles de l’ensemble E:

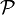
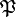
Par exemple si A = {a,b}, (A)={Ø,{a},{b},A}

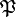
L’existence de l’ensemble des parties est assurée par un axiome, l’axiome de l'ensemble des parties. Cet axiome exprime en substance que pour tout ensemble E, il existe un ensemble F contenant tous les sous-ensembles de E.

L’unicité de l’ensemble des parties est assurée par un autre axiome, l’axiome d'extensionnalité.

L’ensemble des parties d’un ensemble, muni de la réunion, de l’intersection et de l’inclusion forme une algèbre de Boole.

Produit cartésien

Le produit cartésien, noté (lire " A croix B "), de deux ensembles A et B est l’ensemble des couples dont la première composante vient de A et la seconde de B :

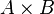
On a pour A et B finis:

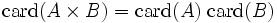
Différence entre produit cartésien dénombrable et non-dénombrable, axiome du choix, argument de la diagonale de Cantor

Somme disjointe

La réunion disjointe de deux ensembles A et B ne doit pas être confondue avec leur somme disjointe, notée ou  :

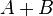
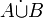
Les symboles et dans la définition précédente peuvent être remplacés par d’autres, par exemple et . La seule exigence est que les deux symboles utilisés différent l’un de l’autre.

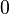
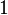
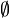
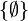
La somme disjointe a été conçue pour que, contrairement à la réunion, le cardinal de son résultat soit toujours la somme des cardinaux des ensembles concernés :

Elle peut être utilisée comme substitut à la notion de couple d’ensembles, surtout quand ces ensembles sont susceptibles d’être des classes.

Exponentiation

On définit comme l’ensemble des applications de E dans F.

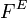
On peut alors identifier l’ensemble des parties d’un ensemble E, , à  ; cela revient en effet à identifier chaque partie de E à son indicatrice.

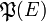
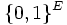
On peut aussi considérer le produit cartésien comme étant l’ensemble E^I.