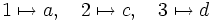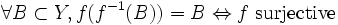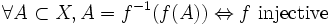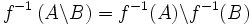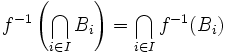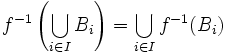Image réciproque - Définition

L'image réciproque d'une partie B d'un ensemble Y par une application est le sous-ensemble de X constitué des éléments dont l'image par f appartient à B : .

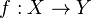
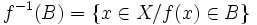
Exemple : Considérons l'application , définie par

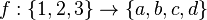
L'image réciproque de {a,b} par f est f ^{− 1}({a,b}) = {1}.

Notons qu'avec cette définition, f^-1 devient une fonction dont l'ensemble de définition est l'ensemble de toutes les parties de Y et dont l'ensemble d'arrivée est l'ensemble des parties de X.

Mise en garde : Lorsque f est une bijection, il ne faut pas confondre cette opération sur les parties avec l'application réciproque f_-1. Fort heureusement, l'image réciproque par f s'identifie avec l'image directe par f^-1.

Propriétés élémentaires

• Pour toutes parties B₁ et B₂ de Y,

.

.

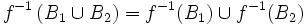
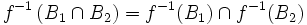
• pour toute partie B de Y, .

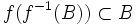
• pour toute partie A de X,

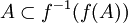
• pour toutes parties A et B de Y,

• Pour toute famille de parties de Y,

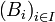
Nous disons en général qu' " avec l'image réciproque tout est possible ".