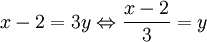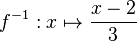Application réciproque - Définition

En mathématiques, une application réciproque est en des termes simples une fonction qui " fait exactement l'inverse de ce que fait une application donnée ". L'application réciproque permet de retrouver un élément à partir de son image par une application donnée; autrement dit une application réciproque défait ce que l'application originale a fait.

Exemple

Considérons la fonction .

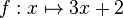
On pose :

y = 3x + 2

On inverse le couple (x,y) :

x = 3y + 2

Et on isole y :

L'application réciproque est donc :

L'exposant " -1 " n'est pas une puissance et f ^{− 1} ne correspond pas à l'inverse d'une fonction pour la multiplication, mais à l'inverse pour la composition de fonctions. On trouve aussi les notations et f^r qui lèvent cette ambiguïté.

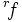
En fait, pour qu'une fonction f admette une application réciproque, elle doit être bijective :

1. chaque élément de l'ensemble d'arrivée doit être atteint par f : sinon il n'y aurait pas de moyen de définir l'image par f ^{− 1} de certains éléments.
2. chaque élément de l'ensemble d'arrivée doit être atteint une seule fois par f : sinon l'application réciproque enverrait cet élément sur plus qu'une seule valeur.

Définition formelle

Formellement, l'application réciproque d'une application bijective f d'un ensemble X sur un ensemble Y, est l'application notée f^-1 qui à un élément y de l'ensemble d'arrivée Y, associe l'unique antécédent x de y par f.

• pour tout x de X, , car f(x) a pour unique antécédent x
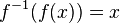
• pour tout y dans Y, , car f envoie l'unique antécédent de y sur y.

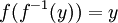
Ce que nous pouvons écrire : et .

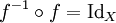
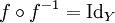
Il est possible de définir l'application réciproque d'une fonction pas forcément bijective, en considérant l'application g de même ensemble de définition que f dont l'ensemble d'arrivée est restreint à l'image de f et qui envoie un élément sur l'image de cet élément par f; l'application réciproque est alors l'application multiforme qui à un élément de l'image de f associe ses antécédents par f.

Soient I et J deux parties de et une fonction bijective. Si nous représentons graphiquement la fonction f dans un repère cartésien, alors le graphe de f ^{− 1} est le symétrique orthogonal de celui de f par rapport à la droite d'équation y = x.

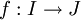
Algébriquement, nous déterminons l'application réciproque de f en résolvant l'équation

y = f(x)

d'inconnue x, et en échangeant y et x pour obtenir

y = f ^{− 1}(x).

Cela n'est pas toujours facile ou possible.

Si la fonction f est analytique, alors le théorème d'inversion de Lagrange peut être utilisé.