Théorie mathématique de la percolation - Définition

Le modèle mathématique de la percolation a été introduit par Hammersley en 1957. Il s'intéresse aux caractéristiques des milieux aléatoires, plus précisément aux ensembles de sommets connectés dans un graphe aléatoire.

Informellement, imaginons que l'on place de l'eau au sommet d'une pierre spongieuse. S'il y a assez de petits canaux, il est alors possible qu'il y ait un chemin du centre de la pierre vers l'extérieur. Ce modèle permet de répondre à ce genre de question.

Différents types de percolation

Cette théorie s'applique à la science des matériaux, dans le domaine de la percolation.

Description du modèle de base

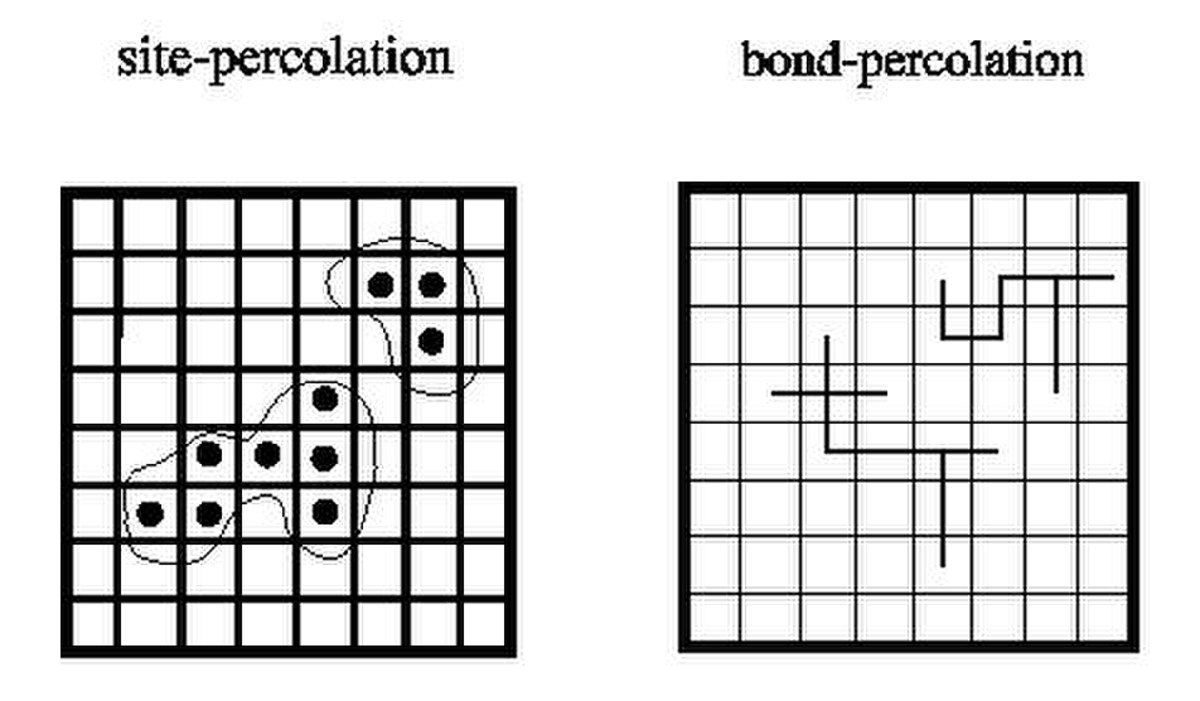
Nous considérons le réseau d-dimensionnel Z^d. Les arêtes sont les couples de points à distance euclidienne 1. Nous fixons ensuite un paramètre p compris entre 0 et 1. Chaque arête est alors ouverte avec probabilité p et fermée avec probabilité 1 − p, ceci indépendamment les unes des autres. La dénomination ouverte signifie que l'arête est gardée, alors que fermée signifie qu'elle est enlevée. On note P_p la mesure obtenue.

On s'intéresse à l'existence d'un chemin infini dans le graphe aléatoire ainsi obtenu. Une quantité essentielle est la probabilité de percolation : . Par des arguments de couplage, il est aisé de démontrer que θ est une fonction croissante de p.

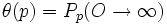
Il existe un point critique p_c tel que θ(p) est nulle si p < p_c et strictement positive si p > p_c. En dimension deux, Harry Kesten a démontré qu'on a p_c = 1 / 2.

Le régime sous-critique p < p_c

Dans ce régime, il n'y a pas de chemin infini dans le graphe. Les composantes connexes (appelé aussi clusters) finis sont généralement de petite taille. Plus précisément la probabilité que le cluster contenant le point x ait une taille qui dépasse n décroît exponentiellement vite avec n. En particulier, la taille moyenne d'un cluster est finie.

Le régime critique p = p_c

Ce régime est encore mal connu (à l'exception notable de la dimension 2). On conjecture que θ(p_c) = 0, c’est-à-dire qu'il n'y a pas de percolation au point critique, mais ceci n'est pour l'instant démontré qu'en dimension deux ou en grande dimension d > 18. En particulier, le cas de la dimension trois, dont la pertinence physique est évidente, demeure non prouvé.

Le régime sur-critique p > p_c

Dans la phase surcritique, il y a une unique composante infinie de points connectés. Cependant, les clusters finis sont généralement de petite taille. Le cluster infini rencontre tout l'espace; plus précisément la proportion de points d'une boîte de taille n qui appartiennent au cluster infini tend vers θ(p_c) > 0 lorsque n tend vers l'infini. On sait aussi que le cluster infini est très rugueux: la proportion des points d'une boîte de taille n qui sont à la frontière du cluster infini parmi la totalité des points du cluster infini qui sont dans cette boïte tend vers 1 − p lorsque n tend vers l'infini.

Autres modèles

• La percolation orientée qui à des liens avec le processus de contact
• La percolation FK qui permet de relier la percolation au modèle d'Ising et au modèle de Potts.
• La percolation de premier passage

Livres de références

• Percolation de G.R. Grimmett chez Springer
• Percolation Theory for Mathematicians de Harry Kesten chez Birkhaüser
• Introduction to Percolation Theory, Taylor and Francis Ed. London, 1985