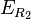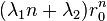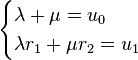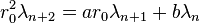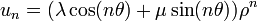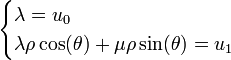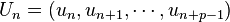Suite récurrente linéaire - Définition

En mathématiques, on appelle suite récurrente linéaire d’ordre p, toute suite à valeurs dans un corps K (généralement ou ) définie pour tout par la relation de récurrence suivante :

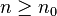
a₀, a₁, …a_{p − 1} étant p scalaires fixés de K (a₀ non nul), pour tout , on a

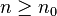
Une telle suite est entièrement déterminée par la donnée des p premiers termes de la suite et par la relation de récurrence

Les suites récurrentes linéaires d’ordre 1 s’appellent plus simplement des suites géométriques de raison a₀. Les suites récurrentes linéaires d’ordre 2 sont entièrement connues et leur terme général est déterminé en fonction des coefficients a₀ et a₁. Une des suites de ce type est la très célèbre suite de Fibonacci. L’étude des suites récurrentes linéaires d’ordre p fait appel à la notion d’espace vectoriel et au calcul matriciel.

Suite récurrente linéaire d’ordre 1

• Voir article détaillé : Suite géométrique

Si la relation de récurrence est u_{n + 1} = qu_n, le terme général est

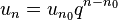
Suite récurrente linéaire d’ordre 2

a et b étant deux scalaires fixés de K avec b non nul, la relation de récurrence est

u_{n + 2} = au_{n + 1} + bu_n (R)

On va prouver que le terme général d'une telle suite est

• si r₁ et r₂ sont deux racines distinctes du polynôme X² − aX − b
• si r₀ est racine double du polynôme X² − aX − b
• pour une suite réelle quand ρe^iθ et ρe ^{− iθ} sont les deux racines complexes du polynôme X² − aX − b

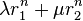
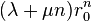
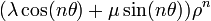
On ne perd rien à la généralité de la suite en supposant que celle-ci est définie sur tout et pas seulement à partir de n₀. En effet, si une suite (u) n’est définie qu’à partir de n₀, elle induit la création d’une suite (v) définie sur en posant .

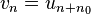
L’idée est alors de rechercher des suites géométriques vérifiant la récurrence (R). C’est-à-dire chercher des scalaires r tels que la suite vérifie (R). On démontre aisément que ce problème équivaut à résoudre l’équation du second degré . Le polynôme est alors appelé le polynôme caractéristique de la suite. Son discriminant est . Il faudra alors distinguer plusieurs cas, selon que le nombre de racine du polynôme caractéristique.

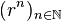
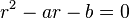
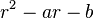
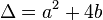
Si le polynôme possède deux racines distinctes

Soient r₁ et r₂ les deux racines distinctes . Les suites et vérifient (R) ainsi que toute suite dont le terme général serait (cela tient au caractère linéaire de la récurrence). A-t-on alors trouvé toutes les suites vérifiant (R) ? Une suite vérifiant (R) étant entièrement déterminée par la donnée de u₀ et u₁, il suffit de prouver que l’on peut toujours trouver λ et μ solutions du système

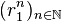
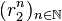
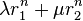
Or ce système a pour déterminant r₂ − r₁ non nul. Il est donc toujours possible d’exprimer une suite vérifiant (R) comme combinaison linéaire des suites et

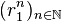
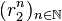
Cette situation se produit pour toute suite à valeurs réelles pour laquelle le discriminant est strictement positif, ou pour toute suite à valeurs complexes pour laquelle le discriminant est non nul.

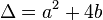
Si le polynôme possède une racine double

Si le discriminant est nul, le problème est tout autre car on ne trouve qu’une seule valeur r₀, donc une seule famille de suites géométriques vérifiant (R) . L’idée consiste alors à rechercher les suites telles que, pour tout entier n, avec vérifiant (R). Cette méthode s’appelle la méthode de variation de la constante. On s’assure d’abord de l’existence de la suite en vérifiant que r₀ n’est jamais nul . La relation de récurrence sur se traduit par une relation de récurrence sur  :

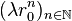
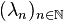
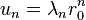
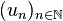
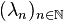
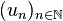
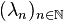
En utilisant ensuite le fait que a² + 4b = 0 et que , on obtient la relation caractéristique de toute suite arithmétique :

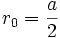
λ_{n + 2} − λ_{n + 1} = λ_{n + 1} − λ_n

La suite est donc une suite arithmétique de terme général

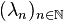
λ_n = λ + μn.

Les suites vérifiant (R) ont alors pour terme général :

.

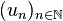
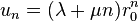
Ce résultat s'applique pour des suites à valeurs réelles ou complexes pour lesquelles le discrimant du polynôme caractéristique est nul.

Si le polynôme ne possède pas de racine

C'est le cas pour les suites à valeurs réelles pour lesquelles le discriminant du polynôme caractéristique est strictement négatif. L’équation du second degré possède alors dans deux racines conjuguées.

et .

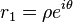
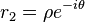
Les suites de terme général sont des suites complexes vérifiant (R). Parmi celles-ci, celles pour lesquelles A et B sont conjugués, sont des suites réelles . Donc les suites de terme général

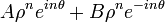
sont des suites réelles vérifiant (R) (on a pris A = λ / 2 − iμ / 2). A-t-on alors trouvé toutes les suites vérifiant (R) ? Une suite vérifiant (R) étant entièrement déterminée par la donnée de u₀ et u₁, il suffit de prouver que l’on peut toujours trouver λ et μ solutions du système

Or ce système a pour déterminant ρsin(θ) non nul. Il est donc toujours possible d’exprimer une suite vérifiant (R) comme combinaison linéaire des suites et .

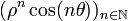
Suite récurrente d’ordre p

Sous-espace vectoriel de dimension p

Si on appelle (R_p) la relation de récurrence :

pour tout entier n,

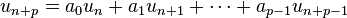
et si on appelle , l’ensemble des suites à valeurs dans K et vérifiant (R_p), on démontre que est un sous-espace vectoriel de l’ensemble des suites à valeurs dans K. Cela tient à la linéarité de la relation de récurrence.

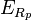
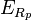
De plus, ce sous espace vectoriel est de dimension p. En effet, il existe un isomorphisme d’espace vectoriel entre et l’ensemble  : à chaque suite (u) de , on associe le p_uplet . Il suffit alors de connaître une famille libre de p suites vérifiant (R_p) , l’ensemble est alors engendré par cette famille libre.

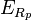
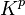
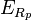
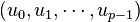
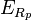
Terme général

La recherche du terme général et des suites particulières s’effectue en travaillant sur K^p . À chaque suite on associe la suite telle que

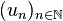
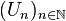
La relation de récurrence sur induit une relation de récurrence sur

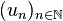
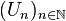
U_{n + 1} = AU_n où

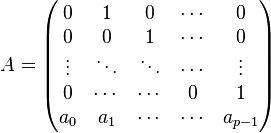
Le terme général de la suite U est alors déterminé par

U_n = AⁿU₀

Le problème semble alors terminé. Mais la réelle difficulté consiste alors à calculer Aⁿ... On préfère plutôt déterminer une base de .

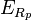
Recherche d'une base

Le polynôme caractéristique de la matrice A est . Ce n'est pas un hasard si on le retrouve pour caractériser les suites vérifiant R_p.

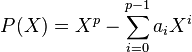
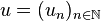
On note f la transformation linéaire qui, à une suite associe la suite définie par v_n = u_{n + 1}. La condition u vérifie R_p se traduit alors par P(f)(u) = 0. L'ensemble est donc le noyau de P(f). Si P est un polynôme scindé dans K (ce qui est toujours vrai si ), il existe k racines et k exposants tel que . Le noyau de P(f) est alors la somme directe des noyaux des . Il suffit donc de trouver une base de chacun de ces noyaux pour déterminer une base de .

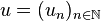
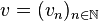
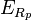
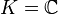
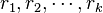
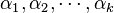
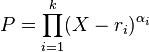
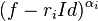
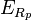
On peut montrer que toute suite de terme général est élément du noyau de pour peu que le degré de Q soit inférieur strictement à α_i. Cette démonstration se fait par récurrence sur α_i. Comme les suites , pour j = 0 à α_i − 1 forment une partie libre de α_i éléments, la famille de toutes les suites , pour j = 0 à α_i − 1 et pour i = 1 à k forme une famille libre de éléments de (de dimension p) donc une base de . Les éléments de sont donc des sommes de suites dont le terme général est avec degré de Q strictement inférieur à α_i.

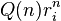
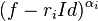
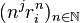
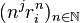
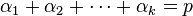
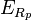
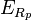
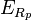
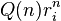
Retour à la récurrence d'ordre 2

Si le polynôme caractéristique se scinde en (X − r₁)(X − r₂) alors les polynômes Q sont de degré 0 et les éléments de sont des suites dont le terme général est .

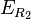
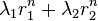
Si le polynôme caractéristique se scinde en (X − r₀)² alors les polynômes Q sont de degré 1 et les éléments de sont des suites dont le terme général est .