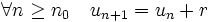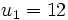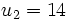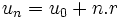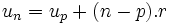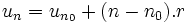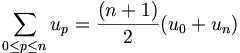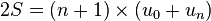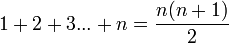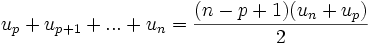Suite arithmétique - Définition

En mathématique, une suite arithmétique est une suite définie sur à valeurs dans un groupe additif E telle qu'il existe un élément de appelé raison pour lequel :

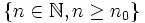
En pratique ou . Mais on peut tout aussi bien rencontrer des suites arithmétiques à valeurs dans un espace vectoriel.

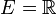
On dit alors que les termes sont en " progression arithmétique ".

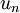
Exemple Si la raison et  :

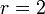
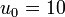
Terme général

Si E est un groupe et si est une suite arithmétique de E de raison alors, pour tout  :

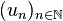
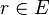
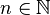
Plus généralement, si la suite est définie sur et si n et p appartiennent à A alors :

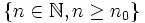
Une suite arithmétique est donc entièrement déterminée par la donnée de son premier terme et par sa raison r.

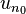
Réciproquement, une suite définie sur par

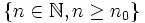
est une suite arithmétique de raison r.

En analyse réelle ou complexe, la suite arithmétique est l'aspect discret de la fonction affine.

Sens de variation et convergence

Ce paragraphe concerne les suites arithmétiques à valeurs dans .

Si r > 0 la suite est croissante, si r < 0 la suite est décroissante et si r = 0 la suite est constante.

En général (si r est non nul), la suite arithmétique est divergente. Cependant elle admet une limite:

• si r > 0 sa limite est
• si r < 0 sa limite est .
• Si la raison est nulle, la suite est constante et converge vers la constante.

Somme des termes

Si ou et si est une suite arithmétique de E alors, pour tout  :

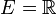
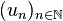
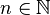
La légende veut que la méthode de calcul fut inventée par Carl Friedrich Gauss, élève dissipé qu'il s'agissait d'occuper et à qui l'on aurait confié la tâche de calculer la somme de tous les entiers de 1 à 100. En écrivant la somme deux fois, dans un ordre différent, il obtint :

S = 1 + 2 + 3 + .... + 98 + 99 + 100

S = 100 + 99 + 98 + ...+ 3 + 2 + 1

Puis, remarquant que 100 + 1 = 99 + 2 = 98 + 3 = ... = 101, il obtint facilement

2S = 100 × 101 donc S = 50 × 101.

Légende ou réalité, cette astuce est la méthode de démonstration pour calculer les somme des termes:

S = u₀ + u₁ + ... + u_n

S = u_n + u_{n − 1} + ... + u₀

Remarquant que u_p + u_{n − p} = u₀ + u_n, il vient

Cette propriété s'applique pour calculer la somme des n premiers entiers

et se généralise à toute somme de termes consécutifs d'une suite arithmétique

Elle se généralise aussi à toute suite à valeurs dans un espace vectoriel sur un corps de caractéristique différente de 2