Inégalité de Bienaymé-Tchebychev - Définition
Soit X une variable aléatoire de moyenne μ et de variance finie σ2 (l'hypothèse de variance finie garantit l'existence de la moyenne).
L'inégalité de Bienaymé-Tchebychev affirme que, pour tout réel strictement positif α :
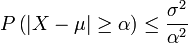
La démonstration n'est qu'une simple application de l'Inégalité de Markov

















































