Espace probabilisable - Définition

Un espace probabilisable est un couple formé d'un ensemble Ω, d'une tribu ou σ-algèbre sur Ω.

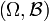
L'ensemble Ω est appelé l'univers et les éléments de sont appelés les évènements.

Exemples:

• Soit Ω un univers quelconque ; est un espace probabilisable. Cet exemple est important puisque si Ω est dénombrable alors toute tribu engendrée par les évènements élémentaires est nécessairement égale à
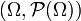
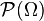
• Soit Ω un univers quelconque; est un espace probabilisable ( est la tribu grossière).

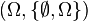
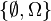
Dans la pratique, l'univers Ω se définit en fonction de l'expérience aléatoire effectuée, et la tribu se choisit en fonction des évènements concernés par le problème.

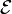
Si nous décidons de travailler dans la tribu grossière, nous ne pourrons considérer que l'évènement certain et l'évènement impossible. Lorsque l'univers est fini ou dénombrable, on choisit le plus souvent la tribu discrète : .

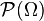
Lorsque, sur un espace probabilisable, on définit une probabilité, l'espace probabilisable devient un espace probabilisé.