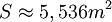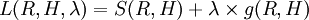Multiplicateur de Lagrange - Définition

Le multiplicateur de Lagrange est une méthode permettant de trouver des points stationnaires (maximum, minimum...) d'une fonction dérivable d'une ou plusieurs variables.

Cette technique est utile entre autres pour résoudre les problèmes d'optimisation sous contrainte(s) (linéaire(s)). Supposons que le problème soit de trouver un extremum d'une fonction de N variables, tout en imposant K contraintes sur les valeurs de celle-ci. La méthode consiste à introduire une inconnue scalaire supplémentaire - appelée multiplicateur de Lagrange - par contrainte; il y a donc K multiplicateurs. On forme ensuite une combinaison linéaire de la fonction et des contraintes, où les coefficients des contraintes sont les multiplicateurs de Lagrange. Le problème passe ainsi d'un problème d'optimisation avec contrainte à un problème non contraint, qui peut être résolu par une méthode adaptée (gradient conjugué, par exemple).

Hugh Everett a généralisé la méthode aux fonctions non-dérivables, sous réserve de disposer d'un algorithme déterminant l'optimum (ou les optima) d'une fonction sans contrainte (dans la pratique, on doit se contenter d'heuristiques).

Écriture du problème

Soit le problème d'optimisation :

où

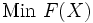
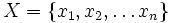
soumis à des contraintes d'égalité

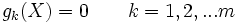
Si le nombre m de contraintes est supérieur au nombre n de variables, le problème est surcontraint et n'admet en général pas de solution.

La méthode des multiplicateurs de Lagrange stipule qu'on atteint la valeur optimale de F(X) pour les valeurs x_i de X qui satisfont le système :

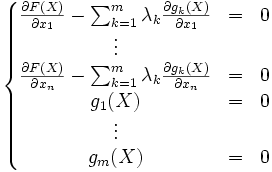
Cette méthode peut être généralisée aux problèmes d'optimisation incluant des contraintes d'inégalités (ou non linéaires) en utilisant les conditions de Kuhn-Tucker. Mais également sur des fonctions discrètes à maximiser ou minimiser sous contraintes, moyennant un changement d'interprétation, en utilisant la méthode des multiplicateurs d'Everett (ou de Lagrange généralisés), plus volontiers appelée méthode des pénalités.

Exemple

Supposons que l'on veuille déterminer le rayon R et la hauteur H d'un cylindre qui minimise la surface S de celui-ci, tout en ayant un volume V imposé. Le problème s'écrit sous la forme :

Minimiser

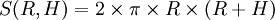
sous

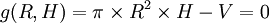
Ayant une seule contrainte, on ajoute un seul multiplicateur de Lagrange :

Le problème revient maintenant à minimiser le Lagrangien

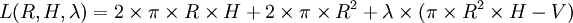
On cherche donc à annuler le Gradient du Lagrangien, soit : ,

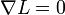
ce qui nous amène au système :

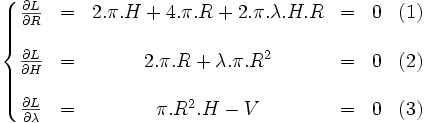
L'équation (2) nous donne :

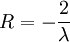
L'équation (1) nous donne :

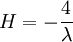
L'équation (3) nous donne enfin :

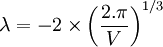
Si le volume imposé est V = 1m³, l'optimum de la fonction S est :

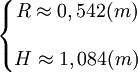
Et la fonction vaut en ce point.