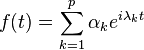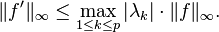Série de Fourier - Définition
En analyse, les séries de Fourier sont un outil fondamental dans l'étude des fonctions périodiques. C'est à partir de ce concept que s'est développé la branche des mathématiques connue sous le nom d'analyse harmonique.
L'étude d'une fonction périodique par les séries de Fourier comprend deux volets. L'analyse consiste en la détermination de la suite de ses coefficients de Fourier. La synthèse permet de retrouver, en un certain sens, la fonction à l'aide de la suite de ses coefficients.
Au-delà du problème de la décomposition, la théorie des séries de Fourier établit une correspondance entre la fonction périodique et les coefficients de Fourier. De ce fait, l'analyse de Fourier peut être considérée comme une nouvelle façon de décrire les fonctions périodiques. Des opérations telles que la dérivation s'écrivent simplement en termes de coefficients de Fourier. La construction d'une fonction périodique solution d'une équation fonctionnelle peut se ramener à la construction des coefficients de Fourier correspondants.
Les séries de Fourier ont été introduites par Joseph Fourier en 1822, mais il fallut un siècle pour que les analystes dégagent les outils d'étude adaptés : une théorie de l'intégrale pleinement satisfaisante et les premiers concepts de l'analyse fonctionnelle. Elles font encore actuellement l'objet de recherches actives pour elles-mêmes, et ont suscité plusieurs branches nouvelles : analyse harmonique, théorie du signal, ondelettes...
Les séries de Fourier se rencontrent usuellement dans la décomposition de signaux périodiques, dans l'étude des courants électriques, des ondes cérébrales, dans la synthèse sonore, le traitement d'image...
Approche intuitive
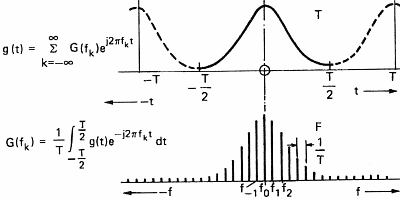
Une fonction F d'une variable réelle est dite périodique de période T lorsqu'elle vérifie : pour tout réel x, f(x + T) = f(x). La fréquence F est l'inverse de la période : F=1/T.
Les fonctions périodiques de période T les plus faciles à étudier sont les fonctions sinusoïdales dont la fréquence est un multiple de F
-
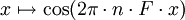
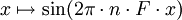
Polynômes trigonométriques
Une combinaison linéaire de ces fonctions sinusoïdales élémentaires porte le nom de polynôme trigonométrique et constitue aussi une fonction périodique de période T. Elle peut se réécrire comme combinaison linéaire de fonctions
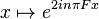
Un polynôme trigonométrique P s'écrit donc sous la forme
Le coefficient d'ordre n peut être obtenu par le calcul suivant :
-
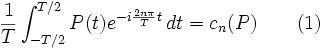
On peut supposer pour simplifier que la période T est
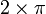
Maintenant multiplions P(x) par e − imx, pour un certain m. En développant, on obtient des termes de la forme cn(P)ei(n − m)x.
À chaque fois que p = n − m donne une valeur non-nulle, le résultat du calcul d'intégral est nul puisque . Ces termes ne contribuent donc pas dans (1).
Inversement, lorsque m = n, le terme considéré est exactement cn(P).
Dans cette formule, les coefficients cn(P) sont nuls à partir d'un certain rang et la somme redonnant P est en fait finie.
Principe des séries de Fourier
Pour des raisons de dimension, on ne peut pas obtenir toutes les fonctions périodiques de période T comme une telle combinaison.
L'idée sous-jacente à l'introduction des séries de Fourier est de pouvoir obtenir une fonction T-périodique, par exemple continue, comme somme de fonctions sinusoïdales :
avec les coefficients cn(f), appelés coefficients de Fourier de f, définis par la formule :
-
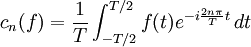
Il s'agit cette fois-ci d'une véritable somme infinie, c'est-à-dire d'une limite de somme finie, ce qui correspond au concept de somme de série.
De nombreux calculs se traduisent de façon très simple sur les coefficients des polynômes trigonométriques, comme le calcul de dérivée. Il est possible de les généraliser au niveau des coefficients de Fourier généraux.
Au sens strict, la formule de décomposition n'est pas correcte en général. Elle l'est, ponctuellement, sous de bonnes hypothèses de régularité portant sur f. Alternativement, on peut lui donner sens en se plaçant dans les bons espaces fonctionnels.
Aspects historiques
Les séries de Fourier constituent la branche la plus ancienne de l'analyse harmonique, mais n'en demeurent pas moins un domaine vivant, aux nombreuses questions ouvertes. L'étude de leurs particularités est allée de pair, pendant tout le XIXe siècle, avec les progrès de la théorie de l'intégration.
Les origines
Les premières considérations sur les séries trigonométriques apparaissent vers 1400 en Inde, chez Madhava, chef de file de l'école du Kerala[1]. En Occident, on les trouve au XVIIe siècle chez James Gregory, au début du XVIIIe chez Brook Taylor. C'est l'ouvrage de ce dernier, Methodus Incrementorum Directa et Inversa, paru en 1715, qui donne le coup d'envoi à l'étude systématique des cordes vibrantes et de la propagation du son, thème de recherche majeur pendant tout le siècle.
Une controverse éclate dans les années 1750 entre d'Alembert, Euler et Daniel Bernoulli sur le problème des cordes vibrantes. D'Alembert détermine l'équation d'onde et ses solutions analytiques. Bernoulli les obtient également, sous forme de décomposition en série trigonométrique. La controverse porte sur la nécessité de concilier ces points de vue avec les questions de régularité des solutions. Selon J.-P. Kahane[2], elle aura un rôle majeur dans la genèse des séries de Fourier.
Bernoulli avait introduit des séries trigonométriques dans le problème des cordes vibrantes pour superposer des solutions élémentaires.
Joseph Fourier (1768-1830) introduit l'équation de la chaleur dans un premier mémoire en 1807[3] qu'il complète et présente en 1811 pour le Grand prix de Mathématiques. Ces premiers travaux, controversés sur le plan de l'analyse, ne furent pas publiés. En 1822, Fourier expose les séries et la transformation de Fourier dans son traité Théorie analytique de la chaleur. Il énonce qu'une fonction peut être décomposée sous forme de série trigonométrique, et qu'il est facile de prouver la convergence de celle-ci. Il juge même toute hypothèse de continuité inutile[4].
En 1829, Dirichlet (1805-1859) donne un premier énoncé correct[5] de convergence limité aux fonctions périodiques continues par morceaux ne possédant qu'un nombre de fini d'extrema. Dirichlet considérait que les autres cas s'y ramenaient ; l'erreur sera corrigée par Jordan en 1881.
En 1848, Wilbraham est le premier à mettre en évidence le phénomène de Gibbs[6] en s'intéressant au comportement des séries de Fourier au voisinage des points de discontinuité.
Avancée conjointe des séries de Fourier et de l'analyse réelle
Le Mémoire sur les séries trigonométriques de Bernhard Riemann (1826-1866), publié en 1867[7], constitue une avancée décisive. L'auteur lève un obstacle majeur en définissant pour la première fois une théorie de l'intégration satisfaisante. Il démontre notamment que les coefficients de Fourier ont une limite nulle à l'infini, et un résultat de convergence connu comme le théorème de sommabilité de Riemann.
Georg Cantor (1845-1918) publie une série d'articles sur les séries trigonométriques entre 1870 et 1872, où il démontre son théorème d'unicité. Cantor raffine ses résultats en recherchant des "ensembles d'unicité", pour lesquels son théorème reste vérifié. C'est l'origine de l'introduction de la théorie des ensembles.
En 1873, Du Bois-Reymond (1831-1889) donne le premier exemple de fonction continue périodique dont la série de Fourier diverge en un point[8]. Le dernier quart du XIXe siècle voit relativement peu d'avancées dans le domaine des séries de Fourier ou de l'analyse réelle en général, alors que l'analyse complexe connaît une progression rapide.
Dans un note de 1900[9] et dans un article de 1904[10], Fejér ( 1880-1959) démontre son théorème de convergence uniforme utilisant le procédé de sommation de Cesàro (moyenne arithmétique des sommes partielles de Fourier). Surtout, il dégage un principe nouveau : l'association systématique entre régularisation au moyen d'un "noyau" et procédé de sommation pour la série de Fourier.
De nouveaux outils d'étude
Henri Lebesgue (1875-1941) donne à la théorie des séries de Fourier son cadre définitif en introduisant une nouvelle théorie de l'intégration. Dans un série de publications qui s'étalent de 1902 à 1910, il étend les théorèmes de ses prédécesseurs, notamment le théorème de Riemann sur la limite des séries de Fourier. Il prouve également plusieurs théorèmes de convergence nouveaux. La plupart de ses résultats figurent dans ses Leçons sur les séries trigonométriques publiées en 1906.
En 1907, Pierre Fatou 1878-1929) démontre l'égalité de Parseval dans le cadre général des fonctions de carré sommable. La même année, Frigyes Riesz (1880-1926) et Ernst Fischer (1875-1954), de façon indépendante, prouvent la réciproque. Ces résultats participent à la naissance d'un domaine nouveau, l'analyse fonctionnelle.
Dorénavant, les questions de convergence dans les espaces fonctionnels sont envisagées à travers l'étude des propriétés des suites de noyaux et des opérateurs associés. Une grande partie des résultats passe par des questions d'estimation de normes appelées "constantes de Lebesgue", qui deviennent un objet d'étude systématique.
Parallèlement, le problème de la convergence simple des séries de Fourier donne lieu à plusieurs coups de théâtre avec la publication de résultats qui ont connu un grand retentissement et surpris les contemporains. En 1926, Andreï Kolmogorov (1903-1987) construit un exemple de fonction intégrable dont la série de Fourier diverge partout[11]. En 1966, Lennart Carleson (1928) établit au contraire [12] que la série de Fourier d'une fonction de carré sommable converge presque partout vers cette fonction. D'autres résultats (Kahane et Katznelson 1966, Hunt 1967) viennent compléter l'étude. Les recherches se portent ensuite sur la convergence des séries de Fourier à plusieurs dimensions, encore imparfaitement connue.
Spectre en fréquences
Une analyse de Fourier porte sur une fonction d'une variable réelle f, périodique, à valeurs réelles ou complexes, de période T. On note F l'inverse de T appelée fréquence fondamentale ou fréquence du fondamental.
La fonction f peut être supposée continue par morceaux, hypothèse suffisante pour exposer beaucoup de résultats intéressants, et qui s'applique à de nombreux cas concrets. Cependant la définition des coefficients de Fourier peut être étendue sans modification au cas d'une fonction périodique intégrable au sens de Lebesgue sur une période. Pour une fonction périodique, être de classe Lp implique l'intégrabilité.
Coefficients complexes
Les coefficients de Fourier (complexes) de f (pour
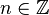
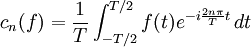
Par périodicité de l'intégrande, ces coefficients peuvent également être calculés en effectuant l'intégrale sur n'importe quel segment de longueur T :
-
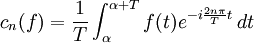
Si n>0, on appelle harmonique de rang n de la fonction f la fonction sinusoïdale de fréquence nF obtenue en tenant compte des coefficients de Fourier d'indice n et -n, donnée par :
-
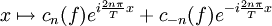
Pour n=0, le coefficient c0(f) n'est autre que la valeur moyenne de f.
La série de Fourier de f est la série de fonctions obtenue en sommant les harmoniques successifs, autrement dit la série de fonctions :
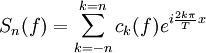
Une des questions à laquelle répond la théorie de Fourier est de déterminer le mode de convergence de cette série (convergence ponctuelle, convergence uniforme, convergence quadratique, ...).
Coefficients réels
Si la fonction f est à valeurs réelles, il peut être intéressant de manipuler des coefficients réels, afin d'éviter de faire appel aux complexes. On définit ainsi les coefficients de Fourier réels de f :
-
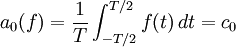
- b0(f) = 0 ;
- Pour n>0,
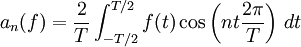
- Pour n>0,
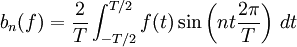
Dans la pratique, il peut être judicieux d'intégrer sur un intervalle de longueur T autre que [-T/2,T/2].
L'harmonique de rang n se réécrit alors comme la fonction :
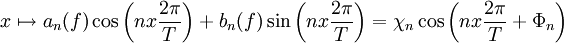
où χn et Φn modulo 2π dépendent explicitement des an(f) et bn(f).
Attention : certains auteurs préfèrent écrire :
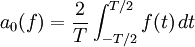
Les relations entre les an, les bn et les cn sont données comme suit :
-
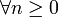
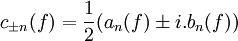
- Pour n > 0, an(f) = cn(f) + c − n(f) et i.bn(f) = cn(f) − c − n(f).
Les dernières identités restent vraies pour n = 0 sous la convention du coefficient en 2 / T.
Caractérisation des fonctions par les coefficients de Fourier
Si deux fonctions intégrables ont la même analyse en fréquences (mêmes coefficients de Fourier), elles sont alors égales presque partout. Dans le cas continu par morceaux, elles coïncident en tous les points sauf un nombre fini. Cette unicité découle des propriétés de densité des polynômes trigonométrique qui sera établie par exemple par le théorème de Fejér ci-dessous. Par suite, seules les fonctions continues, 2π-périodiques, sont égales entre elles si et seulement si leurs coefficients de Fourier sont égaux.
En particulier, les seules fonctions continues dont tous ses coefficients de Fourier sont nuls sauf un nombre fini sont exactement les polynômes trigonométriques.
La parité d'une fonction se traduit sur les coefficients de Fourier :
- ainsi une fonction f est paire, si et seulement si c-n(f)=cn(f) pour tout n.
-
- Si en outre f est réelle, cette propriété devient bn(f) = 0 pour tout n.
- une fonction f est impaire, si et seulement si c-n(f)=-cn(f) pour tout n
-
- Dans le cas réel cela donne an(f) = 0 pour tout n.
Égalité de Parseval
Pour une fonction T-périodique continue par morceaux, ou plus généralement de carré intégrable sur une période, l'égalité de Parseval affirme la convergence de la série suivante et l'identité :
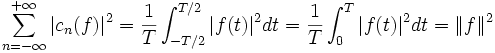
Ce résultat est équivalent à une convergence en moyenne quadratique des séries de Fourier correspondantes (voir ci-dessous).
L'égalité de Parseval implique en particulier que les coefficients de Fourier de f tendent (suffisamment vite) vers 0 en l'infini. Suivant les hypothèses de régularité sur f, la vitesse de convergence peut être précisée (voir ci-dessous).
Reconstitution des fonctions
Une des questions centrales de la théorie est celle du comportement de la série de Fourier d'une fonction et en cas de convergence de l'égalité de sa somme avec la fonction initialement considérée. Sous des hypothèses de régularité convenables, une fonction périodique peut effectivement se décomposer comme somme de fonctions sinusoïdales.
Théorème de convergence ponctuelle (de Dirichlet)
Pour une fonction périodique f de période T, continue en un réel x, et dérivable à droite et à gauche en x, le théorème de Dirichlet affirme la convergence de sa série de Fourier évaluée en x et donne l'égalité :
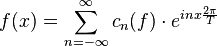
Si f est à valeurs réelles, l'égalité ci-dessus se réécrit avec les coefficients de Fourier réels :
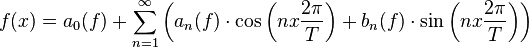
Les hypothèses peuvent être affaiblies. La fonction f peut seulement être continue à gauche et à droite en x et à variation bornée sur un voisinage de x. Dans ce cas, f(x) doit être remplacé par la valeur moyenne de f en x, soit donc la moyenne entre ses limites à droite et à gauche en x. La démonstration du théorème se base sur le fait que la série de Fourier se calcule par produit de convolution avec un polynôme trigonométrique aux propriétés remarquables : le noyau de Dirichlet.
Théorème de convergence uniforme de Dirichlet
Le théorème de convergence uniforme de Dirichlet est une version globale du théorème de convergence ponctuelle. Pour une fonction T-périodique et continument dérivable au voisinage d'un segment I, la série de Fourier de f converge uniformément vers f sur I.
La démonstration consiste à constater que les constantes dans les estimations de la preuve dut théorème de convergence ponctuelle peuvent être choisis indépendamment du point d'évalutation
En particulier, pour les fonction continument dérivable et T-périodique, sa série de Fourier converge uniformément sur
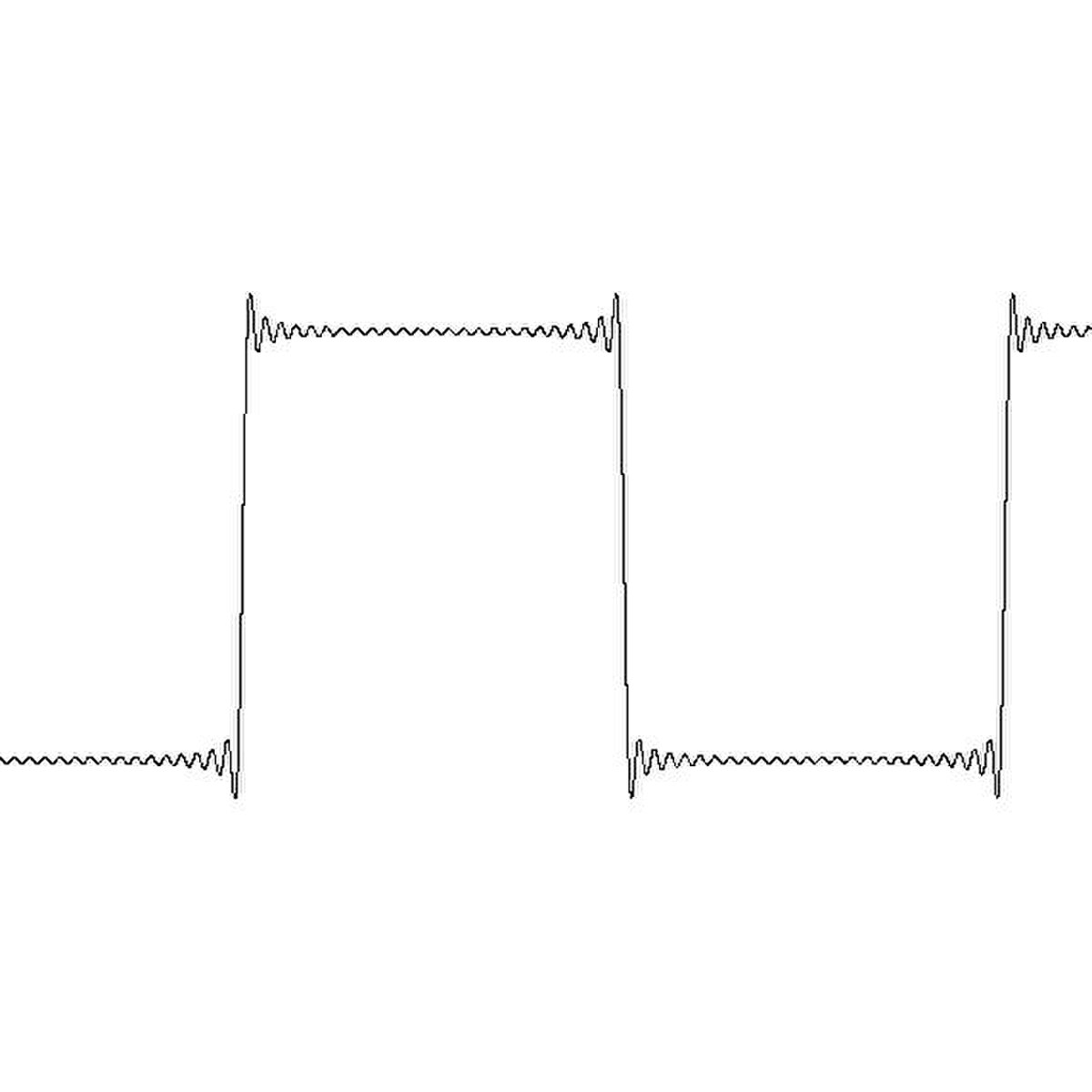
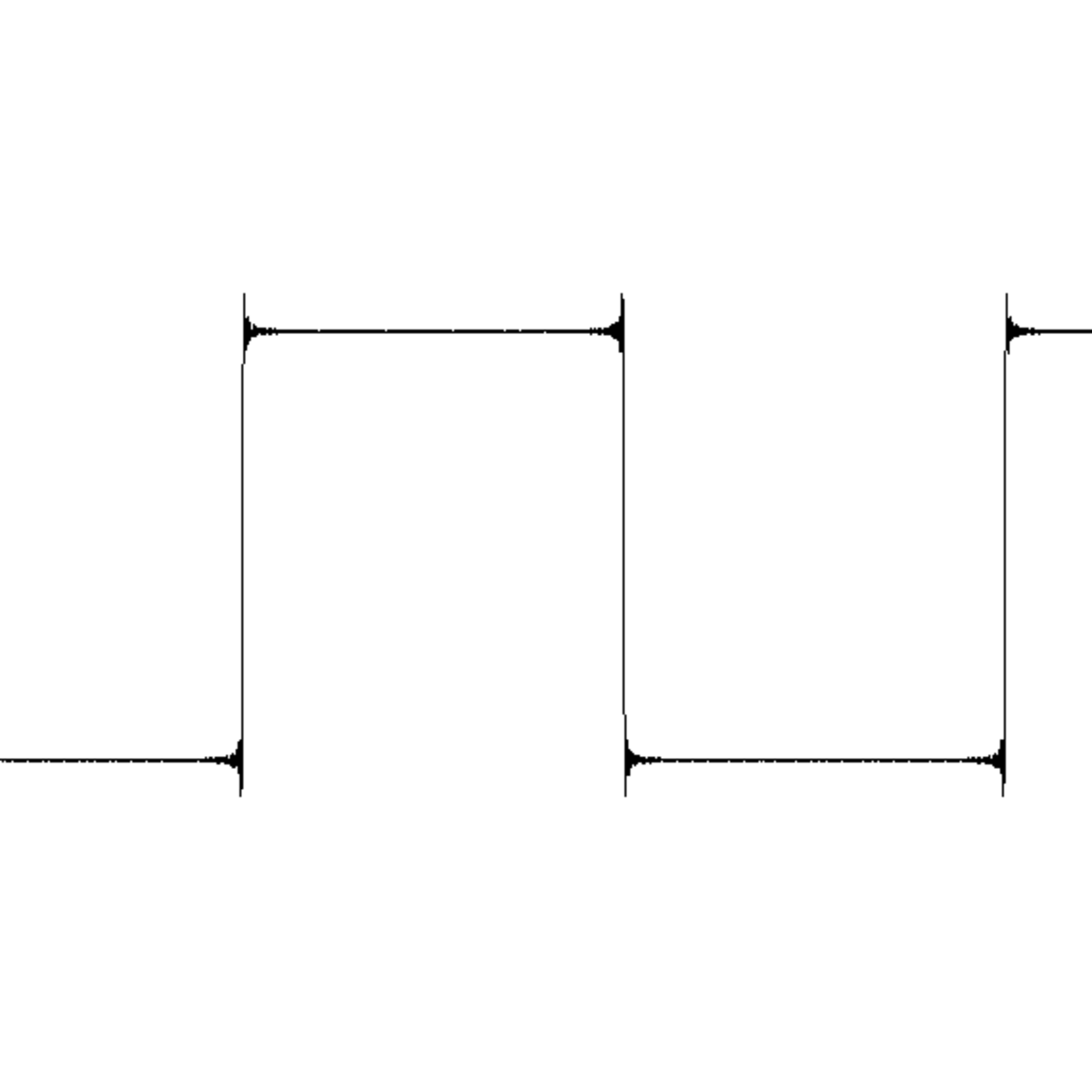
Phénomène de Gibbs
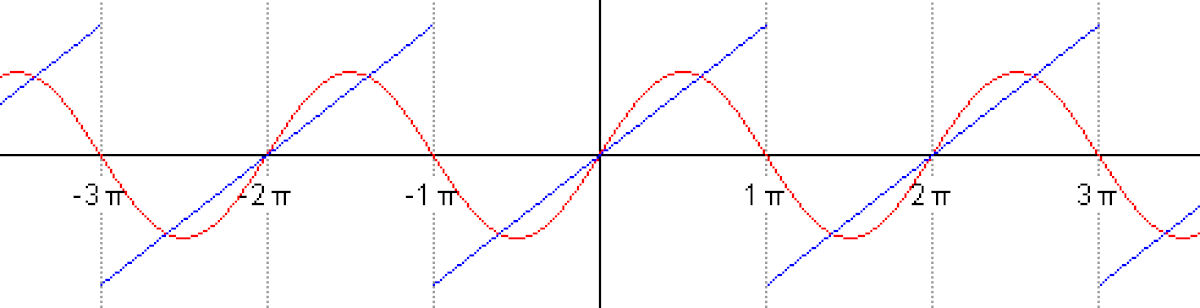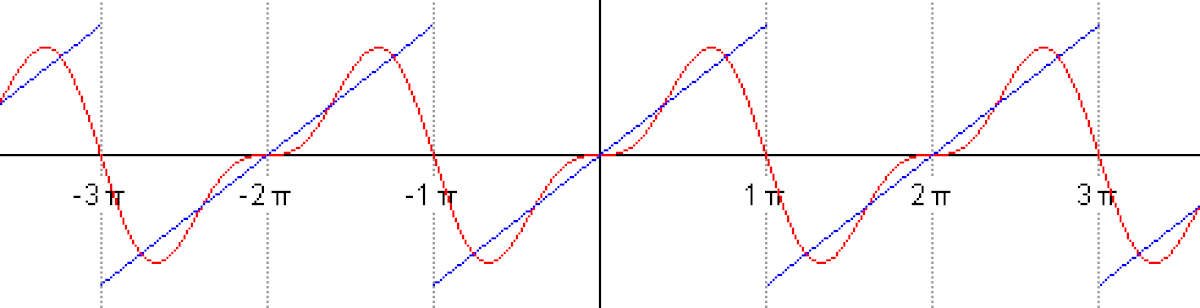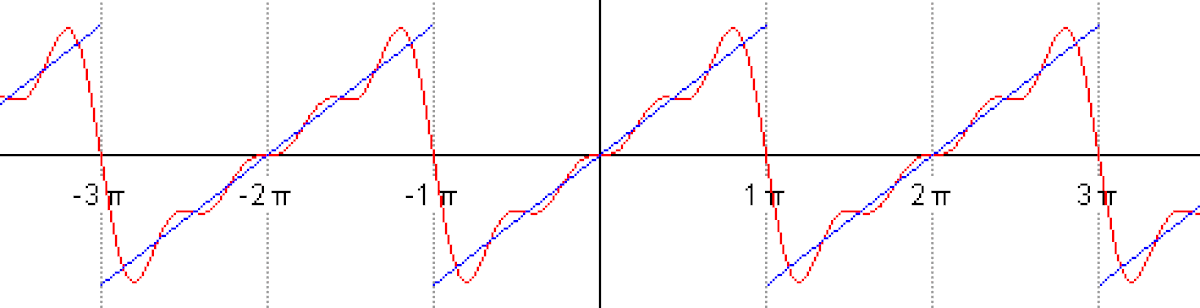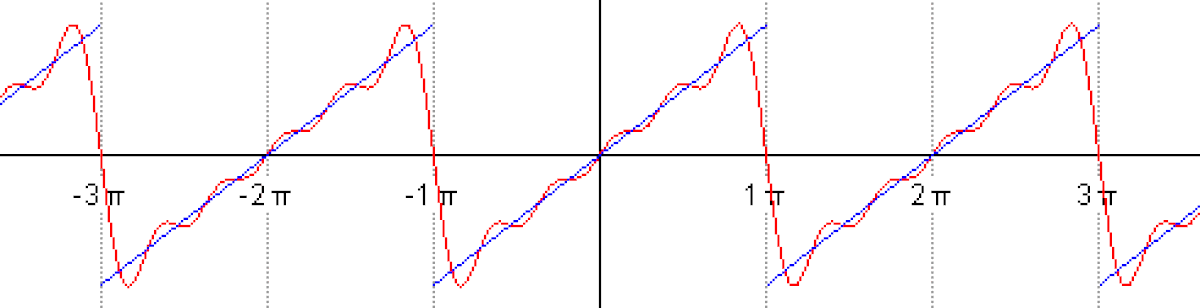
Le phénomène de Gibbs est un effet de bord observé au voisinage d'une discontinuité de la fonction. Pour l'illustrer, voici la représentation des termes d'ordre 10,50,250 de la série de Fourier de la fonction "créneau".
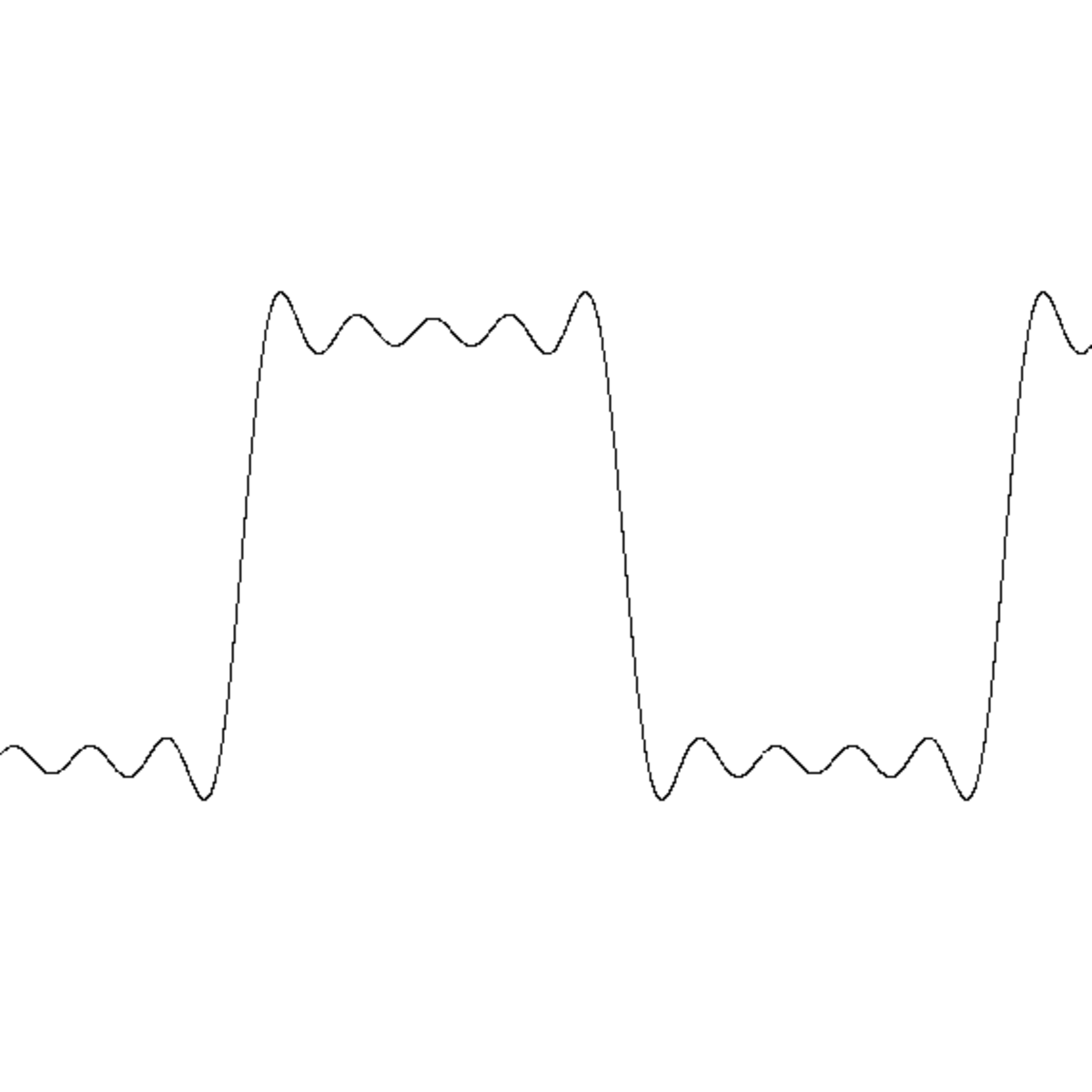
Approximation du créneau à l'ordre 10
|
Le polynôme trigonométrique n-ème terme de la série de Fourier, Sn(f), est une fonction continue, il est donc normal qu'il ne puisse approcher uniformément la fonction créneau qui, elle, ne l'est pas. Sur une des zones de "plateau", en dehors d'un voisinage de la discontinuité, cependant, la série de Fourier converge uniformément vers la fonction (elle en est indiscernable sur le dernier graphique).
Au niveau du point de discontinuité, Sn subit une forte oscillation, une sorte de "sursaut". Les images laissent soupçonner et le calcul montre effectivement que l'amplitude de ce sursaut tend vers une constante. Précisément si la fonction a une discontinuité d'amplitude Δy, alors Sn, tout en restant continue, connaîtra un "saut" en ordonnée valant de l'ordre de 18% de plus.
Note : un phénomène analogue peut être analysé lorsqu'on étudie les polynômes d'interpolation de Lagrange lorsque le nombre de points d'interpolation tend vers l'infini : c'est le phénomène de Runge.
Convergence en moyenne quadratique
La convergence en moyenne quadratique concerne la convergence pour la norme hermitienne :
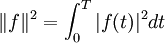
Cette norme est définie par exemple sur l'espace E des fonctions T-périodiques et continues, ou sur l'espace F des fonctions T-périodiques mesurables de carré intégrable identifiées modulo égalité sur un ensemble négligeable. La norme dérive du produit scalaire :
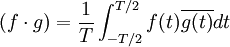
L'espace E est dense dans l'espace F et l'espace normé F est complet ; il peut être obtenu comme le complété de E.
Introduisons la fonction exponentielle complexe d'indice n
-
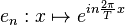
La famille (en) forme une famille orthonormale. Cette famille est notamment libre. L'espace qu'elle engendre est l'espace des polynômes trigonométriques, sous-espace de E. Le n-ième coefficient de Fourier de f est le produit scalaire de f par en :
En particulier, le n-ième polynôme trigonométrique de f est la projection orthogonale de f sur l'espace engendré par
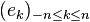
- La famille (en) est une base de Hilbert : le sous-espace des polynômes trigonométriques est dense dans E et dans F.
- La série de Fourier d'une fonction T-périodique de carré intégrable sur une période converge en nome L2 vers la fonction considérée.
Une conséquence est l'égalité de Parseval.
Théorème de Fejér
Le théorème de Féjer consiste à améliorer la convergence donnée par le théorème de convergence uniforme de Dirichlet en effectuant une limite de Césaro des sommes partielles de la série de Fourier. Pour une fonction continue et T-périodique, on note :
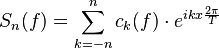
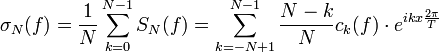
Le théorème de Féjer affirme que, sous la seule hypothèse de continuité, la suite des fonctions σN(f) converge uniformément vers f.
Ce théorème de Fejér constitue une démonstration possible de la version trigonométrique du théorème de Stone-Weierstrass. Il se démontre en utilisant les propriétés d'un polynôme trigonométrique particulier : le noyau de Fejér d'indice n est positif et la suite de ces noyaux constitue une approximation de l'identité.
σN(f) est un polynôme trigonométrique admettant des fréquences s'étalant de − nf à nf. Pour chaque fréquence, le coefficient précédent est modifié. Les nouveaux coefficients tendent à donner plus d'importance aux petites fréquences et à amortir les termes de fréquence élevée, ce qui permet de lisser les comportements trop brusques.
Convergence simple
Les résultats positifs obtenus en envisageant d'autres modes de convergence ne font pas perdre sa pertinence à l'étude de la convergence simple.
Dans le cadre des fonctions continues, le théorème de Fejér permet d'affirmer que si la série de Fourier de f converge simplement, alors elle admet pour limite la fonction f. En revanche des considérations d'analyse fonctionnelle permettent de prouver qu'il existe une fonction continue dont la série de Fourier diverge en au moins un point : précisément il s'agit d'une application du théorème de Banach-Steinhaus à l'opérateur de convolution par la fonction noyau de Dirichlet. Il est également possible d'en donner des exemples explicites simples. C'est ainsi le cas de la fonction 2π-périodique définie par
Les domaines de divergence possibles sont connus grâce à deux théorèmes complémentaires.
- D'une part, selon un théorème de Kahane et Katznelson, pour tout ensemble de mesure de Lebesgue nulle, on peut trouver une fonction continue dont la série de Fourier diverge en tout point de cet ensemble[13].
- D'autre part, selon le théorème de Carleson, la série de Fourier d'une fonction continue converge presque partout vers cette fonction.
Si on élargit le cadre aux fonctions intégrables sur une période,
- le théorème de Kolmogorov assure qu'il existe une fonction intégrable dont la série de Fourier diverge en tout point,
- en revanche le théorème de Lennart Carleson cité plus haut a été prouvé dans le cadre des fonctions L2 et possède même une extension aux espaces Lp pour p>1[14]. Pour de telles fonctions, la série de Fourier de f converge presque partout.
Applications
Calculs de séries
L'application des théorèmes de Dirichlet et de Parseval, précédemment énoncés, permettent de calculer la valeur exacte de la somme de séries numériques remarquables, parmi lesquelles :
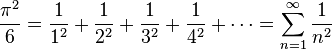
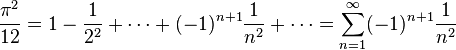
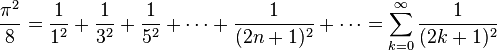
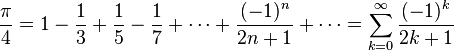
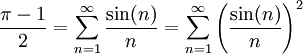
La valeur de la série numérique
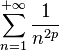
Par exemple avec f périodique de période 2π, valant
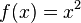
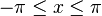
-
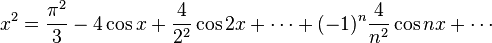
- Dans cette identité, si l'on fait x = π, on retrouve la célèbre formule démontrée par Euler :
-
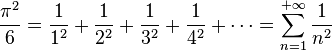
- pour x=π/2 on a également un résultat remarquable :
-
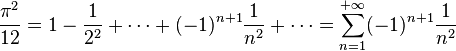
Par ailleurs la formule de Parseval donne
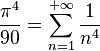
En prenant d'autres fonctions, telles que :
- le signal carré périodique :
![x \mapsto \left\{\begin{array}{cl} -1 & \mbox{si } x \in [-\pi;0[ \\ 0 & \mbox{si } x = 0 \\ 1 & \mbox{si } x \in ]0;\pi[\end{array}\right.](https://static.techno-science.net/illustration/Definitions/autres/c/c606d74e59376b60d66bd9502059f491_c160ac9671978564996198c7e015affc.png)
- le signal triangulaire périodique :
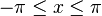
Équations aux dérivées partielles
Inégalités fonctionnelles
L'analyse de Fourier permet de donner des expressions nouvelles pour l'opération de dérivation, et d'en tirer des estimées intéressantes.
Ainsi l'inégalité de Wirtinger s'applique à une fonction f de classe
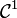
-
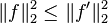
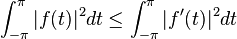
Ce résultat peut servir à son tour à établir le théorème isopérimétrique : le cercle est la courbe fermée enserrant un domaine connexe d'aire maximale pour une longueur donnée.
Un autre exemple d'application est l'inégalité de Bernstein. Celle-ci s'applique à une fonction de la forme suivante
avec des coefficients αk complexes et des coefficients λk réels (ce n'est donc pas nécessairement un polynôme trigonométrique) et distincts. L'inégalité permet de comparer cette fois les bornes supérieures de f et de sa dérivée :
La démonstration de l'inégalité de Bernstein réside sur l'écriture de f′ comme une combinaison infinie de translatées de f, à l'aide d'une formule d'analyse de Fourier.
Comportement des coefficients
Effet des opérations sur les coefficients
Pour une fonction continue et
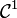
-
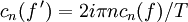
Plus généralement, pour une fonction de classe
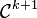
- cn(f(k + 1)) = (2iπn / T)k + 1cn(f).
Coefficients et régularité de la fonction
- Le théorème de Riemann-Lebesgue montre que les coefficients de Fourier d'une fonction f intégrable sur une période tendent vers 0 lorsque n tend vers l'infini.
- L'identité de Parseval admet une réciproque : une fonction est de carrés sommable sur une période si et seulement si la série des carrés des modules des coefficients de Fourier converge. C'est le théorème de Riesz-Fischer
- Il existe peu de caractérisations analogues pour d'autres espaces fonctionnels. On peut affirmer cependant qu'une fonction périodique est
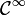
-
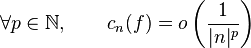
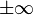
- Plus précisément, si la fonction est de classe
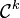
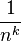
- Réciproquement, si les coefficients de Fourier sont dominés par
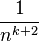
Extension du concept de série de Fourier
Extension aux distributions
Les séries de Fourier se définissent par analogie pour les distributions. Une distribution D est par définition une application linéaire sur l'espace des fonctions. D est dite T-périodique lorsque sa valeur sur une fonction test f et sur sa T-translatée. Dans ce cas, il existe une distribution à support compact d telle que D est la somme de la série suivante au sens des distributions :
-
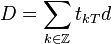
Les coefficients de Fourier de D sont alors définis comme suit :
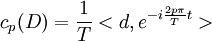
Ces coefficients ne dépendent pas du choix de d. Ils sont " à croissance lente ", c'est-à-dire dominés par une expression polynomiale.
La série de Fourier converge vers D au sens des distributions :
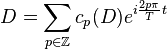
Réciproquement, si on considère une suite à croissance lente, la série trigonométrique correspondante converge au sens des distributions vers une distribution périodique. Un exemple d'utilisation est le peigne de Dirac.
Espaces de Hilbert
Les espaces de Hilbert sont les espaces vectoriels munis d'un produit scalaire et qui sont complets pour la norme associée. L'espace des fonctions T-périodiques, de carré sommable, identifiées par la relation d'égalité presque partout, possède une structure de ce type. Identité de Parseval et théorème de Riesz-Fischer montrent que les fonctions trigonométriques élémentaires forment une base hilbertienne, et les coordonnées d'une fonction sont données par ses coefficients de Fourier.
Tout espace de Hilbert séparable et de dimension infinie E est muni d'une telle base, et l'application qui à un élément de l'espace associe ses coefficients (encore appelés "coefficients de Fourier") est une isométrie de E dans l'espace l2.
Il est possible d'envisager également des espaces de Hilbert non séparables, ainsi il existe des coefficients de Fourier-Bohr pour les fonctions presque périodiques. On ne pose alors plus de conditions sur le rapport de fréquences pour les fonctions trigonométriques de référence.
Série et transformation de Fourier
La décomposition en séries de Fourier est également généralisée aux fonctions non périodiques avec la théorie de la transformée de Fourier et la notion de densité spectrale. Pour une présentation élémentaire, voir Analyse spectrale.
Série et transformation de Fourier sont reliées par la formule sommatoire de Poisson.
Notes et références
- ↑ (en) John J. O'Connor et Edmund F. Robertson, Madhava of Sangamagramma, MacTutor History of Mathematics archive. (consulté en 2000)
- ↑ Jean-Pierre Kahane, Pierre-Gilles Lemarié-Rieusset, Séries de Fourier et ondelettes [détail des éditions], p. 33 et suivantes
- ↑ Mémoire sur la propagation de la chaleur dans les corps solides, disparu depuis des archives de l'Institut et connu à travers un abrégé paru sous la signature de Siméon Denis Poisson dans le Nouveau Bulletin des sciences par la Société philomatique de Paris, t. I, p. 112-116, n°6; mars 1808. Paris, Bernard
- ↑ Joseph Fourier, Théorie analytique de la chaleur, voir le texte sur Gallica, alinéa 235 p. 259 et alinéa 417 p. 551
- ↑ Gustav Lejeune-Dirichlet, Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données, Journal de Crelle 4 (1829) p. 157-169
- ↑ Henry Wilbraham, On a certain periodic function, Cambridge Dublin Math. J. 3, 1848
- ↑ Œuvres de Riemann, 2ème édition, p. 230
- ↑ Paul David Gustave Du Bois-Reymond, Eine neue Theorie der Convergenz und Divergenz von Reihen mit positiven Gliedern, Journal für die reine und angewandte Mathematik 76 (1873) p. 61-91.
- ↑ Lipót Fejér, Sur les fonctions intégrables et bornées, C.R. Acad. Sci. Paris, 10 décembre 1900
- ↑ Leopold Fejér, Untersuchungen über Fouriersche Reihen, Math. Annalen, 58, 1904
- ↑ Andreï Kolmogorov, Une série de Fourier-Lebesgue divergente partout, C. R. Acad Sci. Paris, 183, p. 1327-28
- ↑ Lennart Carleson, Convergence and growth of partial sums of Fourier series, Acta Math. 116, p. 135-157
- ↑ J.-P. Kahane, Y. Katznelson, Sur les ensembles de divergence des séries trigonométriques, Studia Math, 26, 305-306
- ↑ R.A. Hunt, On the convergence of Fourier series orthogonal expansions and their continuous analogues, Proc Conf Edwardsville 1967, p 235-255, Southern Illinois University Press, Carbondale, III, 1968
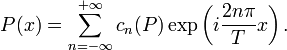
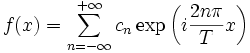
![\forall x\in [-\pi,\pi], \,\, f(x)=\sum_{n=1}^{+\infty} \frac1{n^2} \sin \left(\left(2^{n^3}+1\right)\frac {|x|} 2\right)](https://static.techno-science.net/illustration/Definitions/autres/7/7985516856500f3dbaffc06361a84148_de8d58fc16e1f5571c8a5f0376a25043.png)