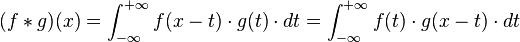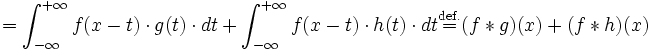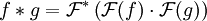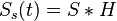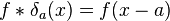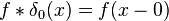Produit de convolution - Définition
En mathématiques, le produit de convolution de deux fonctions réelles ou complexes f et g se note généralement "
On peut considérer cette formule comme une généralisation de l'idée de moyenne mobile.
Pour que cette définition ait un sens, il faut effectuer certaines hypothèses sur f et g, par exemple si ces deux fonctions sont sommables leur produit de convolution est défini pour presque tout x et est lui-même sommable.
Propriété du produit de convolution
- Le produit de convolution est commutatif.
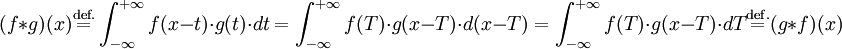
Où T=x-t, soit t=x-T.
- Le produit de convolution est distributif
![(f\ast (g+h)) (x) \stackrel{\mathrm {def.}}{=} \int_{-\infty}^{+\infty} f(x-t) \cdot (g(t)+h(t)) \cdot dt = \int_{-\infty}^{+\infty} [f(x-t) \cdot g(t)+ f(x-t) \cdot h(t)] \cdot dt](https://static.techno-science.net/illustration/Definitions/autres/d/dbb6153bc4bc38c17553dcd2ef11f616_892191719e6505768c5a0f5b7d0797b6.png)
- Le produit de convolution correspond à la multiplication des transformées de Fourier des fonctions
où
Utilisation du produit de convolution
Le produit de convolution est utilisé dans le traitement du signal, lorsque l'on utilise des filtres (passe-bas, passe-haut, passe-bande). Si l'on a un signal entrant S(t) et un élément filtrant ayant une fonction de transfert H(t) alors le signal de sortie Ss(t) sera la convolution de ces deux fonctions :
Une autre utilisation des produits de convolution se situe dans le domaine de la mécanique quantique, où l'on réalise des produits de convolution à partir des fonctions d'onde bra et ket.
De manière générale, on peut écrire les équations différentielles linéaires correspondant à de nombreux problèmes physique sous la forme du produit de convolution d'un opérateur par une fonction décrivant le système. On peut alors résoudre de manière générique le problème en déterminant l'inverse de convolution de l'opérateur (appelé fonction de Green). Joseph Fourier a été à l'origine de cette méthode lorsqu'il a cherché à résoudre l'équation de la chaleur. Sa formulation moderne a du attendre l'arrivée de la théorie des distributions introduite par Laurent Schwartz.
Le produit de convolution se généralise à de nombreuses algèbres d'un groupe, par exemple aux algèbres d'un groupe fini. Si de plus le groupe est abélien, alors la théorie de l'analyse harmonique sur un groupe abélien fini permet d'établir tous les résultats classiques du produit de convolution.
Approche vulgarisée
La manière la plus simple de se représenter le produit de convolution consiste à considérer la Fonction δ de Dirac δa(x) ; cette fonction vaut 0 si x ≠ a, et son intégrale vaut 1. Ceci peut sembler à première vue bizarre, on peut l'imaginer comme la limite d'une suite de fonctions, des courbes en cloche ou des rectangles ayant toutes la même surface 1, mais de plus en plus fines (donc de plus en plus hautes) ; lorsque la largeur des courbes tend vers 0, sa hauteur tend vers +∞, mais la surface reste égale à 1. Pour des raisons pratiques, on représente souvent le dirac comme un bâton positionné en a et de hauteur 1.
Dirac : limite d'une suite de fonctions
Du fait de sa forme, on appelle aussi parfois un dirac " fonction impulsion ". Le produit de convolution par un dirac δa correspond à une translation de la fonction initiale d'une valeur de a
Produit de convolution d'une fonction par un dirac
On voit que δ0 laisse invariant une fonction, c'est l'élément neutre du produit de convolution
Si l'on considère maintenant le produit de convolution par une somme pondérée de diracs (α.δa + β.δb), on obtient la superposition de deux courbes dilatées.
Produit de convolution d'une fonction par une somme pondérée de deux diracs
Considérons maintenant une fonction porte Pa,b ; c'est une fonction qui vaut 1/(b-a) entre a et b, et 0 ailleurs (son intégrale vaut 1). Cette fonction peut être vue comme une succession de diracs. La convolution de f par Pa,b va donc s'obtenir en faisant glisser f sur l'intervalle [a;b]. On obtient un " élargissement " de f.
Produit de convolution d'une fonction par une fonction porte
Si l'on considère maintenant une fonction quelconque g, on peut voir g comme une succession de diracs pondérés par la valeur de g au point considéré. Le produit de convolution de f par g s'obtient donc en faisant glisser la fonction f et en la dilatant selon la valeur de g.
Produit de convolution d'une fonction par une fonction quelconque
Notes et références
Bibliographie
- Bracewell, Ronald N. Convolution Theorem. The Fourier Transform and Its Applications, 3e édition New York : McGraw-Hill, 1999. info sur l'ouvrage sur le site de l'éditeur