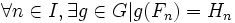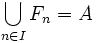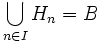Paradoxe de Banach-Tarski - Définition

Le paradoxe de Banach-Tarski, dû à Stefan Banach et Alfred Tarski, montre qu’il est possible de couper une boule de en un nombre fini de morceaux et de réassembler ces morceaux pour former deux boules identiques à la première, à une isométrie près. Il montre qu’il existe des morceaux non-mesurables, sans quoi on obtiendrait une contradiction (la longueur, la surface ou le volume étant des exemples de mesures).

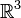
Il remet en cause notre notion intuitive de volume, puisque il n’y pas de " création " de matière, donc il existe des parties de pour lesquelles la notion de mesure (et donc de volume) n’a pas de sens. Cela est aussi " paradoxal " que d'affirmer que l’intervalle [0, 1] contient " autant " de nombres que tout entier.

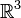
La démonstration de ce paradoxe utilise l’axiome du choix, qui a été et est toujours contesté par certains mathématiciens. Par ailleurs, toute tentative pour exhiber des ensembles non-mesurables utilise cet axiome.

Préliminaires

Le groupe des isométries est l’ensemble de toutes les translations, symétries planaires, rotations et de leur composées, c’est-à-dire l’ensemble de toutes les manières de prendre une figure dans l’espace et de la déplacer ou de la faire tourner sur elle-même sans la déformer (et en particulier sans changer sa taille). Une isométrie peut se voir comme une fonction mathématique g et une figure comme un ensemble de points E. Dire qu’il existe un ensemble F tel que g(E) = F, c’est simplement dire en gros que E et F ont la même forme et la même taille, bref qu’ils sont identiques à leur position près.

Deux ensembles sont donc équidécomposables si on peut couper le premier en morceaux et reconstruire le deuxième simplement en déplaçant les morceaux (c’est-à-dire en leur appliquant une isométrie). Un ensemble est dédoublable s’il est équidécomposable à une " moitié " de lui-même.

Une mesure est en gros une fonction mathématique qui satisfait aux mêmes conditions qu’une longueur. C’est donc une généralisation de la longueur (ou du volume). Un bon exemple de mesure est la mesure de Lebesgue : si on veut mesurer un intervalle, on prend sa longueur et si on a un ensemble " en plusieurs morceaux ", on prend la somme de la longueur de chacun des morceaux. Par exemple, si deux bouteilles d’un litre de vin sont posées à deux endroits différents, physiquement il y a deux objets distincts. C’est ici que le volume montre " ses limites ". Mais mathématiquement on peut considérer que ces deux bouteilles ne forment qu’un seul et même objet dont le volume est 2 litres. C’est typiquement une mesure.

Plus généralement, la mesure d'un " objet " vide vaut 0, alors que la mesure d'un ensemble constitué de plusieurs " objets " est la somme des mesures de chacun des objets. Ce qu'affirme ce paradoxe, c’est qu’on peut construire des ensembles suffisamment " tordus " pour qu’on ne puisse pas les mesurer, c’est-à-dire qu’on ne peut pas leur associer une valeur en général (ou un volume ou une longueur en particulier) sans violer les deux propriétés évoquées plus haut. Plus précisément, si on essaie de trouver une manière de leur associer un volume, on peut prouver qu’en continuant d’appliquer cette méthode, on trouvera une partie qui a le même volume que le tout, ou un verre à eau a le même volume qu’un camion citerne, ce qui est absurde. Donc, il faut reconnaitre que le volume d’un tel ensemble n’existe pas. Bien sûr, il s’agit d’une propriété mathématique, on ne pourra jamais construire physiquement un tel ensemble.

Le paradoxe affirme que l’on peut multiplier les petits pois ou transformer une grenouille en quelque chose de plus gros que le bœuf dès l’instant qu’on passe par une étape où elle est coupée en morceaux non mesurables, où le volume perd son sens. Par la suite, on peut réassembler ces morceaux en un objet " plus gros " sans avoir à dire que la grenouille et le bœuf ont le même volume puisque le volume du résultat n’est pas la somme des volumes des morceaux.

Ce paradoxe a été assez longtemps source d'une rupture entre les mathématiques et la physique, certains y voyaient la preuve que les mathématiques étaient incapables de décrire la nature. En pratique, une telle transformation est impossible avec des objets de la vie courante : elle nécessite des coupures infiniment fines, ce qui est physiquement impossible, à cause de la taille finie des atomes.

En résumé, le paradoxe est faux, car n'est pas une description fidèle de notre univers.

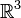
Enoncé plus précis

Soient A, B deux parties d’un ensemble E. On dit que A et B sont équidécomposables suivant un groupe de transformation G s’il existe deux suites finies d’ensembles et telles que :

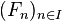
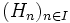
Par exemple, tout parallélogramme est équidécomposable à un rectangle. L’équidécomposabilité est une relation d'équivalence, donc elle est symétrique, réflexive et transitive. À noter ici qu’il n'est pas intéressant d’inclure les homothéties dans G. On prend donc généralement le groupe des isométries (translations et rotations).

Un ensemble E est dit " dédoublable " s’il existe deux ensembles A et B non vides tels que (union disjointe) et tels que A, B, E soient équidécomposables.

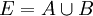
Démontrer le résultat de Banach-Tarski revient à montrer que la boule unité de est dédoublable suivant le groupe des isométries de .

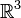
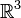
Il faut enfin remarquer le rôle essentiel joué dans ce résultat par la non commutativité du groupe des rotations de l'espace : on démontre que le paradoxe n'est pas possible dans le plan.

Un exemple d’ensemble non mesurable

Soit R une relation d'équivalence définie par .

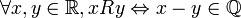
On construit l'ensemble quotient , qu'on note aussi ( dans ce cas, la relation d'équivalence est sous entendue).

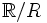
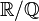
Soit S_n un ensemble tel que S_n contienne un et un seul élément de chaque classe d’équivalence de . On utilise l’axiome du choix, car on ne sait pas construire de fonction de telle qu’elle renvoie un et un seul élément de chaque classe d’équivalence, on est donc obligé de supposer son existence.

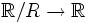
On peut montrer que S_n n’est pas mesurable (c’est-à-dire qu’il n’appartient pas à la tribu de Lebesgue).