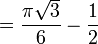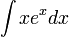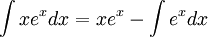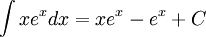Intégration par parties - Définition
En mathématiques, l'intégration par parties est une méthode qui permet de transformer l'intégrale d'un produit de fonctions en d'autres intégrales, dans un but de simplification du calcul.
La formule-type est la suivante, où f et g sont deux fonctions dérivables, de dérivées continues et a et b deux réels de leur intervalle de définition.
ou encore
où u représente une partie de l'intégrande et dv représente l'autre partie ainsi que la variable d'intégration
Démonstration
La démonstration de cette formule est très simple : en effet, elle découle directement de la propriété de dérivation d'un produit de fonctions u et v :
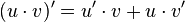
Ce qui donne bien la propriété énoncée ci-dessus.
Cette démonstration peut également être faite à l'aide de la notation de Leibniz. Soit deux fonctions dérivables u et v. La règle de la dérivation d'un produit nous donne :
En multipliant par dx on obtient :
-
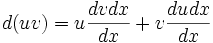
- d(uv) = udv + vdu
On réarrange ensuite l'expression de la façon suivante :
- udv = d(uv) − vdu
Il suffit maintenant d'intégrer l'équation :
On obtient alors :
On peut généraliser cette formule aux fonctions de classe Ck + 1
Il est à noter que la règle employée pour dériver est l'ordre LPET. L'on commence par les fonctions logarithmiques puis polynomiales, exponentielles et enfin trigonométriques.
Exemples
Effectuons le calcul de :
grâce à une intégration par parties. Pour cela, nous posons :
- f(x) = x, de telle sorte que f'(x) = 1,
- g'(x) = cos(x), de telle sorte que g(x) = sin(x), par exemple.
Il vient :
Effectuons le calcul de l'intégrale indéfinie suivante :
Pour l'intégration par parties posons :
- u = x et dv = exdx
Nous avons donc :
- du = dx et v = ex
Utilisons la formule de l'intégration par parties :
L'intégrale est maintenant beaucoup plus simple à calculer. On trouve :
![\int_{a}^{b} f(x) g'(x)\,\mathrm dx = \left[ f(x) g(x) \right]_{a}^{b} - \int_{a}^{b} f'(x) g(x) \,\mathrm dx](https://static.techno-science.net/illustration/Definitions/autres/0/000fad6cd16b2e95f2a4f38eee1ed41d_6a5635ea8bd8c00e0036c1592d4797ed.png)
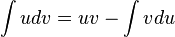
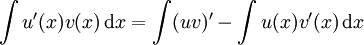
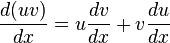
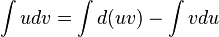
![\int_{a}^{b} f(x) g^{k+1}(x)\,\mathrm dx = \left[ \sum_{n=0}^{k}(-1)^{n} f^{n}(x) g^{k-n}(x) \right]_{a}^{b} + (-1)^{k+1} \int_{a}^{b} f^{k+1}(x) g(x) \,\mathrm dx](https://static.techno-science.net/illustration/Definitions/autres/c/cfe92e5d13a4bb7832ccedae8abeb32d_0b61860cea636c7db4064bee457c67d8.png)
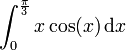
![\int_{0}^{\frac{\pi}{3}} x\cos (x) \,\mathrm dx = \left[ f(x) g(x) \right]_{0}^{\frac{\pi}{3}} - \int_{0}^{\frac{\pi}{3}} f'(x) g(x) \,\mathrm dx](https://static.techno-science.net/illustration/Definitions/autres/4/410e8852636233386c61e3ce5be9eed8_802a77646312b8c65f2e4405137f8a7a.png)
![= \left[x\sin (x)\right]_{0}^{\frac{\pi}{3}} - \int_{0}^{\frac{\pi}{3}} \sin (x) \,\mathrm dx](https://static.techno-science.net/illustration/Definitions/autres/e/ef319de03c304689657b52e5e916895c_100ab120fb55bfd7b2c24e116721e15a.png)