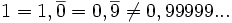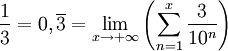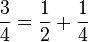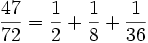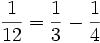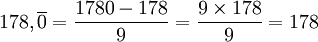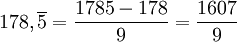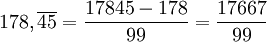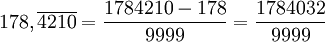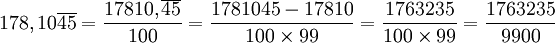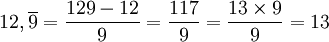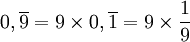Nombre rationnel - Définition

Un nombre rationnel est un nombre réel exprimable par le quotient de deux entiers relatifs ( ), dont le second est non nul. L'ensemble des nombres rationnels est noté .

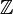
Développement décimal

Comme tous les réels, les rationnels admettent une représentation en développement décimal illimité. Le développement décimal des nombres rationnels a la particularité d'être périodique. C'est-à-dire qu'il existe un suffixe constitué d'une séquence finie de chiffres se répétant continuellement. Cette séquence est appelée : " période du développement décimal illimité ".

Le développement décimal illimité d'un nombre réel, et a fortiori d'un nombre rationnel, est unique si on s'interdit de finir par une séquence périodique composée de ’9’. En effet, dans ce dernier cas, il existera une écriture équivalente se terminant par une période composée de ’0’, et mieux encore, un développement décimal limité équivalent.

Conventionnellement, lorsque nous écrivons un nombre avec les chiffres arabes dans le système décimal nous traçons, s'il y a lieu, une barre horizontale au-dessus de la séquence périodique. Il est aussi possible de mettre un point au-dessus de chaque chiffre de la période, mais cette notation est beaucoup moins utilisée.

Lorsqu'une période est indiquée nous devons faire référence à un nombre rationnel et c'est pour cette raison que d'une manière rigoureuse :

Le développement décimal illimité d'un nombre rationnel est périodique, et réciproquement, un nombre à développement décimal périodique est toujours rationnel.

Ainsi, le nombre (où l'on a des séquences de ’2’ de plus en plus longues) est irrationnel car il n'y a pas de période.

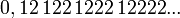
Rationnels, irrationnels

Un nombre réel non rationnel est dit irrationnel.

Ainsi, qui peut s'écrire est rationnel, de même que qui correspond à .

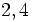
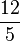
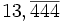
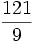
Les nombres entiers sont tous rationnels. En revanche, la racine carrée de 2 est irrationnelle (voir la démonstration).

L'ensemble des nombres réels est l'adhérence de l'ensemble des rationnels : tout réel est la limite d'une suite de rationnels.

Autres écritures

Les nombres rationnels compris entre 0 et 1 peuvent être écrits comme somme de fractions égyptiennes :

Si le dénominateur d'une fraction est un produit de facteurs premiers différents, la fraction peut être décomposée en somme ou différence de fractions partielles :

Les fractions partielles ont des dénominateurs plus simples, qui sont des puissances entières de nombres premiers.

De la notation décimale vers la notation fractionnaire

Il existe une méthode permettant d'écrire un nombre rationnel sous la forme d'une fraction de deux nombres entiers :

Et lorsque la période est décalée :

On peut prouver que en procédant de la sorte :

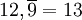
Ou de façon plus intuitive :