Fonction carré - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
La fonction carré est la fonction qui à un nombre réel x associe son carré, noté x², soit x multiplié par lui même. Elle introduit les fonctions puissance, c'est une des plus simples d'entre elles.
Propriétés
- Signe
- La première propriété est la positivité de la fonction. En effet quel que soit x réel,
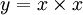
- Parité
- Vient ensuite la parité de la fonction c'est-à-dire que f(x) = f( − x). En effet avec la remarque précédente
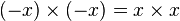
Résolution d'équation de type x² = a
Quand x2 = a, il y a trois cas possibles :
- a < 0 : Aucune solution dans l'ensemble des réels R
- a = 0 : Une solution, x = 0
- a > 0 : Deux solutions,
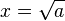
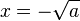
Par exemple, si x2 = 9 alors x = 3 ou x = − 3, car 32 = ( − 3)2 = 9.
Dérivée
La dérivée de la fonction carré est 2x, c'est une fonction affine impaire.
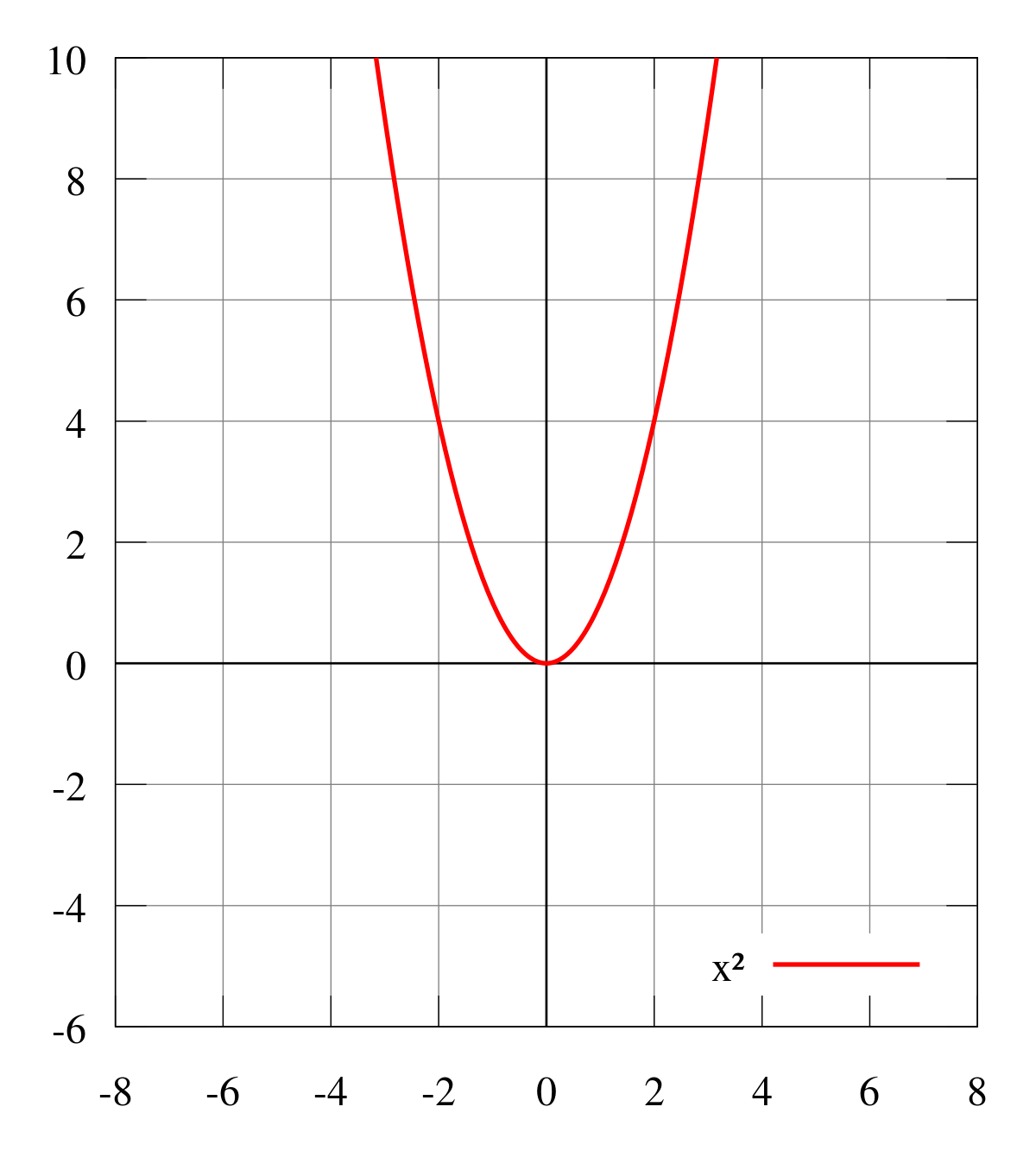
Représentation graphique
Dans un repère orthonormal, la fonction est représentée par une parabole dont le sommet est le point (0,0). On remarque bien que l'intégralité de la parabole se situe au-dessus de la courbe et la parité est décelable grâce à l'axe de symétrie qu'est l'axe des ordonnées.
La fonction carré étant une fonction paire, sa représentation graphique admet un axe de symétrie qui est l'axe des ordonnées.
La fonction carré a pour limite plus l'infini en plus l'infini et en moins l'infini.