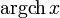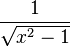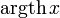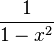Dérivées usuelles - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Cet article énumère les fonctions dérivées de la plupart des fonctions usuelles.
| Domaine de définition
|
Fonction
|
Domaine de définition
|
Dérivée
|
Condition |
|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
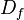
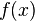
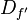
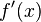
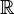

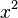
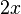
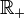
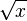
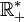
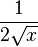
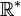

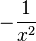
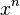
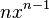
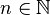
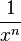
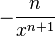
![\sqrt[n]{x} \,\!](https://static.techno-science.net/illustration/Definitions/autres/b/b5c95ce9846444cb91e69c5e262e3200_177defce3b4d4782296bd72d6c2127fc.png)
![\frac{1}{n\sqrt[n]{x^{n-1}}} \,\!](https://static.techno-science.net/illustration/Definitions/autres/c/c87d9ef5f9a8c518a767a909d911d620_f2e94a5eee0530beb370452a950e738e.png)
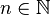
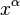
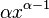
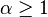
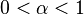
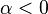
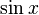
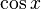
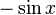
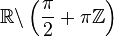
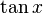
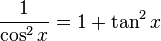
![[ -1 , 1 ] \,\!](https://static.techno-science.net/illustration/Definitions/autres/a/a71529c20010fde4439c76fc6cad81cc_b2c99c1591a53d4dd8a80065075b83fc.png)
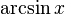
![] -1 , 1 [ \,\!](https://static.techno-science.net/illustration/Definitions/autres/8/8ffb3ae998b0a6623e642306c9b3dddd_a9c1151f3897afa7cf26824eeed532d5.png)
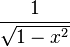
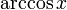
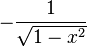
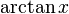
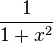
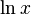
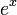
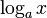
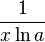
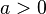
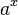
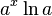
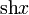

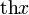
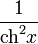
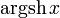
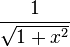
![] 1 , +\infty [ \,\!](https://static.techno-science.net/illustration/Definitions/autres/e/e9beb4fb097a59e14968a8798aa9939a_d3d49ff294b8d4a0bf129d36d5288845.png)