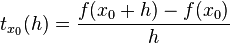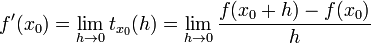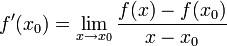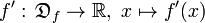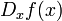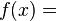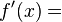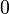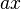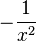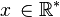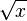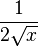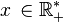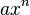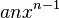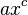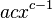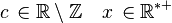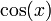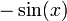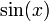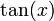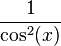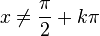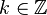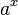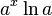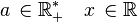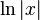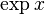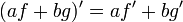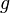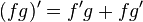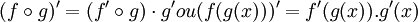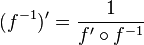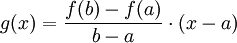Dérivée - Définition
La dérivée d'une fonction est le moyen de déterminer combien cette fonction varie quand la quantité dont elle dépend, son argument, change. Plus précisément, une dérivée est une expression (numérique ou algébrique) donnant le rapport entre les variations infinitésimales de la fonction et les variations infinitésimales de son argument. Par exemple, la vitesse est la dérivée du déplacement par rapport au temps, et l'accélération est la dérivée, par rapport au temps, de la vitesse.
La notion de dérivée a vu le jour au XVIIe siècle dans les écrits de Leibniz et de Newton qui la nomme fluxion et qui la définit comme
" le quotient ultime de deux accroissements évanescents. "
La dérivée de la fonction

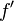
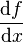
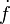
La notion de dérivée est une notion fondamentale en analyse fonctionnelle. Elle permet d'étudier les variations d'une fonction, de construire des tangentes à une courbe et de résoudre des problèmes d'optimisation.
Approche intuitive
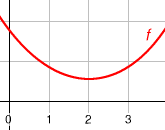
Pour approcher cette notion de manière intuitive, commençons par nous donner une courbe représentative d'une fonction dans un repère cartésien, continue, c'est-à-dire tracée d'un seul trait de crayon, et bien " lisse ", on dira là que la fonction associée est dérivable.
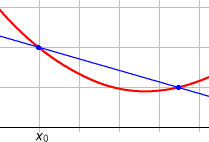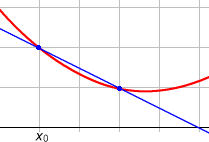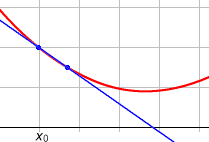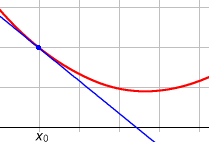
Quel que soit le point que l'on choisit sur la courbe, on pourra alors tracer ce qu'on appelle une tangente, c'est-à-dire une droite qui épouse localement la direction de cette courbe. Concrètement, si l'on trace la courbe et sa tangente et que l'on s'approche en zoomant suffisamment, on aura de plus en plus de mal à distinguer la courbe de sa tangente. On comprend aisément que si la courbe " monte " (ie si la fonction associée est croissante), la tangente sera également montante ; inversement, si la fonction est décroissante, la tangente sera descendante. Si on se donne une abscisse x0 pour laquelle la fonction f est dérivable, on appelle nombre dérivé de f en x0 le coefficient directeur de la tangente à la courbe au point d'abscisse x0. Ce réel donne de précieuses informations sur le comportement local d'une fonction : c'est la mesure algébrique de la vitesse à laquelle cette fonction change lorsque sa variable change. Pour une fonction à plusieurs variables, on parle de la dérivée partielle par rapport à l'une de ses variables.
Ainsi, si le nombre dérivé d'une fonction est positif sur un intervalle, cette fonction sera croissante sur ce même intervalle. Inversement, s'il est négatif, elle sera décroissante. Lorsque le nombre dérivé est nul en un point, la courbe admet une tangente horizontale en ce point.
|
|
Dans l'exemple ci-contre :
|
Approche historique
Dès la seconde moitié du XVIIe siècle, le domaine mathématique de l'analyse numérique connut une avancée prodigieuse grâce aux travaux de Newton et de Leibniz en matière de calcul différentiel et intégral, traitant notamment de la notion d'infiniment petit et de son rapport avec les sommes dites intégrales.
C'est cependant Blaise Pascal qui, dans la première moitié du XVIIe siècle, a le premier mené des études sur la notion de tangente à une courbe - lui-même les appelait " touchantes "; le marquis de l'Hospital participera aussi à la fin du XVIIe à étoffer cette nouvelle théorie, notamment en utilisant la dérivée pour calculer une limite dans le cas de formes indéterminées particulières (cf. Règle de L'Hôpital). Wallis, mathématicien anglais (surtout connu pour la suite d'intégrales qui porte son nom) contribua également à l'essor de l'analyse différentielle.

Néanmoins cette théorie tout juste éclose n'est pas encore pourvue de toute la rigueur mathématique qu'elle aurait exigée, et notamment la notion d'infiniment petit introduite par Newton, qui tient plus de l'intuitif, et qui pourrait engendrer des erreurs dès lors que l'on ne s'entend pas bien sur ce qui est ou non négligeable. C'est au XVIIIe siècle que d'Alembert introduit la définition plus rigoureuse du nombre dérivé en tant que limite du taux d'accroissement - sous une forme semblable à celle qui est utilisée et enseignée de nos jours. Cependant, à l'époque de d'Alembert, c'est la notion de limite qui cette fois-ci pose problème :

C'est au passage à Lagrange (fin du XVIIIe siècle) que l'on doit la notation
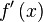
Définition formelle
Soit f une fonction réelle à valeurs réelles définie sur une réunion quelconque d'intervalles non triviaux, et x0 appartenant à l'intérieur de l'ensemble de définition
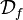
Pour tout
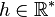
![[x_0,x_0+h]\sub \mathcal{D}_f](https://static.techno-science.net/illustration/Definitions/autres/7/7efa9396caef79651be3b4c2888a9545_76453f5db26dfba1b67366bf15ec5b86.png)
Il s'agit du coefficient directeur de la droite reliant les points de coordonnées (x0,f(x0)) et (x0 + h,f(x0 + h)). Si
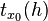
Ou, de manière équivalente :
Une fonction pour laquelle le taux d'accroissement en un point admet une limite (qui est le nombre dérivé) est dite dérivable en ce point.
|
|
Ce calcul de limite revient graphiquement à rechercher la tangente à la courbe en ce point. Ainsi, le nombre dérivé d'une fonction en un point, s'il existe, est égal à la pente de la tangente à la courbe représentative de la fonction en ce point. |
La dérivation peut aussi être définie pour des fonctions d'une variable réelle à valeurs dans d'autres ensembles que

Par exemple, une fonction f d'une variable réelle, à valeurs dans

Fonction dérivée
La dérivabilité est a priori une notion locale (dérivabilité en un point), mais si une fonction est dérivable en tout point d'un intervalle, on peut définir sa fonction dérivée sur l'intervalle en question. La fonction dérivée de f, notée
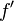
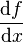
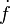
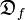
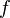

C'est la fonction qui prend en tout point de
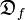

Ainsi, lorsque la fonction dérivable f est croissante, la fonction dérivée
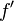
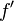
Les fonctions dérivées sont utilisées notamment dans l'étude des fonctions réelles et dans les équations différentielles. Une fonction qui est égale à sa dérivée est dite exponentielle (celle-ci est solution de y' = y, cf. article détaillé).
Notations
Il existe différentes notations pour exprimer la dérivée d'une fonction. On distingue :
- La notation de Lagrange :
- La notation de Leibniz :
-
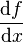
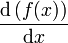
- La notation d'Isaac Newton :
-
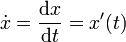
- Enfin, la notation d'Euler :
Dérivée des fonctions usuelles
| Fonctions |
Dérivées |
Conditions |
|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Règles de dérivation

| Nom | Règle | Conditions |
|---|---|---|
| Linéarité |
|
Quelles que soient les fonctions dérivables
|
| Produit |
|
Quelles que soient les fonctions dérivables
|
| Quotient |
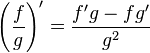
|
Quelles que soient la fonction dérivable
|
| Composée |
|
Quelles que soient les fonctions dérivables (et composables)
|
| Réciproque |
|
Quelle que soit la fonction
|
En particulier, voici les règles courantes se déduisant de la dérivée de composées :
-
Nom Règle Conditions Puissance 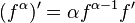
Quel que soit 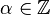
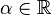
Racine 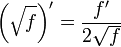
Quelle que soit la fonction dérivable 
Exponentielle 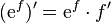
Quelle que soit 
Logarithme 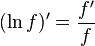
Quelle que soit la fonction dérivable 
Précisons que dans ce dernier tableau, la composée des fonctions g et f n'a pas été notée
Démonstrations
Théorème des accroissements finis
- Énoncé
- Si une fonction ƒ est continue sur un intervalle [a,b] et dérivable sur ]a,b[, alors il existe un point x0 de ]a,b[ tels que la dérivée en ce point est le taux de variation entre a et b
-
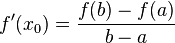
- Démonstration
- On commence par démontrer ceci lorsque ƒ(a) = ƒ(b) : la fonction n'est pas strictement monotone, donc soit la fonction est une droite horizontale et la propriété est valable en tout point, soit la fonction présente un maximum ou un minimum et donc sa dérivée s'annule en un point.
- Pour une fonction quelconque, on se ramène au cas précédent en soustrayant la fonction
-
- alors (ƒ-g)(b) = (ƒ-g)(a) = ƒ(a) et l'on applique la linéarité de la dérivée.
Cette propriété est utilisée en cinématique pour déterminer une approximation du vecteur vitesse à partir d'un relevé de point.
Dérivation de la réciproque d'une fonction
Soit
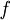
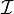
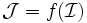
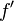
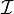
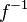
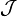
Démonstration:
Montrons que
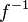
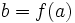
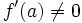
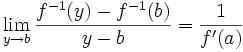
La fonction
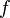
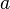
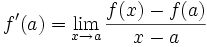
Comme
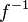
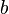
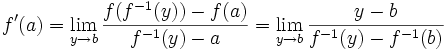
Cette limite étant non nulle, d'après le théorème sur l'inverse d'une limite, on a :
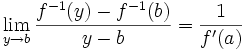
Ou encore :
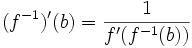
Dérivées de la réciproque des fonctions trigonométriques
On utilise le résultat précédent pour établir :
- Si
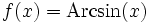
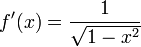
- Si
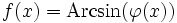
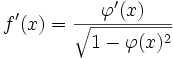
- Si
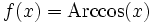
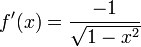
- Si
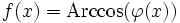
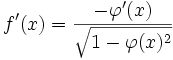
- Si , alors
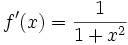
- Si
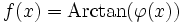
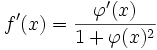

Dérivée d'ordre n
On définit la dérivée d'ordre n pour une fonction n fois dérivable par récurrence :
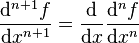
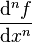
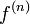
Formule de Leibniz
Si f,g sont des fonctions n fois dérivables, alors :
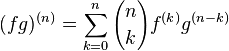
En particulier pour n = 2,
-
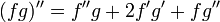
On notera l'analogie avec la formule du binôme de Newton.
Notation de Leibniz
Dérivées des taux de variation liés
Analyse d'une fonction dérivée
En trouvant les valeurs de x où la dérivée vaut 0 ou n'existe pas, on trouve les nombres critiques de la fonction. Les nombres critiques de f permettent de trouver implicitement ses maximums et ses minimums. À effectuer le test de la dérivée première, on construit un tableau de variation ; si le signe de la fonction dérivée passe du plus au moins devant un nombre critique, on a un maximum et si le signe de la fonction dérivée passe du moins au plus devant le nombre critique, on a un minimum. De plus, lorsque le signe de la dérivée première est positif, la fonction monte ; s'il est négatif, elle descend. On ne conclut rien, si au point critique la fonction ne change pas de signe. En dérivant la dérivée première, on a la dérivée seconde. À effectuer le test de la dérivée seconde, on trouve les nombres critiques de la dérivée première pour les placer dans le même tableau ; lorsqu'on observe un changement de signe de la dérivée seconde devant ce ou ces nombres critiques, on dit qu'on a un (ou des) point(s) d'inflexion. Les points d'inflexion marquent un changement de la concavité de la fonction. Un signe positif de la dérivée seconde signifie que la fonction est concave vers le haut et un signe négatif de la dérivée seconde signifie que la fonction est concave vers le bas. Connaissant les changements de concavité et les extrema de la fonction, on peut alors tracer une esquisse du graphique.
Dérivée et optimisation
Méthode pour optimiser un rendement à l'aide du calcul différentiel:
- Mathématisation
- Définitions et dessin : on définit les variables inconnues et on les représente sur un schéma.
- Écrire la fonction objectif à deux variables et préciser si on recherche un maximum ou un minimum dans la situation donnée.
- Trouver la relation entre les deux variables.
- Écrire la fonction objectif à une variable et préciser le domaine de la fonction.
- Analyse
- Dériver la fonction pour obtenir la dérivée première.
- Trouver les nombres critiques de la fonction, où la dérivée première vaut zéro ou n'existe pas dans les intervalles du domaine.
- Effectuer le test de la dérivée première ou le test de la dérivée seconde pour déterminer le maximum ou le minimum recherché de la situation.
- On formule la réponse de façon concise par rapport à la question.
Dérivées et asymptotes
Une fois que l'on a déterminé les asymptotes de la fonction, on peut les noter dans le tableau de variation pour tracer adéquatement l'esquisse du graphique.