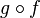Continuité (mathématiques élémentaires) - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
La continuité est une propriété très intuitive des fonctions numériques : on peut dire sans trop se tromper qu'une fonction est continue lorsqu'on peut tracer son graphique " sans lever le crayon ", donc sans faire de " sauts ". On formalise cette notion à l'aide de l'outil des limites.
Fonction continue en un point
On dit qu'une fonction y = f(x) est continue en une valeur a si et seulement si:
1) f(x) est définie
2)
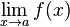
3)
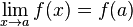
Il est evident que si la condition 3) est satisfaite,les deux premières conditions le sont aussi.
Si cela est vrai uniquement à droite (pour x > a), on dit que f est continue à droite en a. De même à gauche pour x < a.
Dire que f est continue en a revient à dire qu'elle l'est à droite et à gauche en a.
Continuité sur un intervalle
On dit que f est continue sur [a;b] si :
- f est continue sur ]a;b[
- la limite à droite de f lorsque
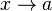
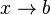
Dérivabilité et continuité
Toute fonction dérivable en un point ou sur un intervalle est également continue sur cet intervalle.
La réciproque est fausse
Corollaire : fonctions usuelles
Les fonctions polynômes, rationnelles (quotients de polynômes) et trigonométriques sont dérivables sur leurs intervalles de définition, et sont donc également continues sur ceux-ci.
De plus, on a continuité de la fonction racine carrée sur
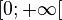

Algèbre des fonctions continues et composée de fonctions continues
Par définition, f est continue en a si et seulement si
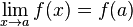
Il résulte donc des théorèmes sur les limites les résultats suivants :
Algèbre des fonctions continues
Soient f et g deux fonctions continues sur un même intervalle I. Alors :
-
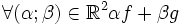
- fg (produit)
-
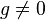
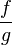
sont continues sur I.
Composée de fonctions continues
Si f est continue sur I et g est continue sur f(I) alors