Théorie de la complexité - Définition

La théorie de la complexité s'intéresse à l'étude formelle de la difficulté des problèmes en informatique. Elle se distingue de la théorie de la calculabilité qui s'attache à savoir si un problème peut être résolu par un ordinateur. La théorie de la complexité se concentre donc sur les problèmes qui peuvent effectivement être résolus, la question étant de savoir s'ils peuvent être résolus efficacement ou pas en se basant sur une estimation (théorique) des temps de calcul et des besoins en mémoire informatique.

Généralités

Machine déterministe et machine non déterministe

Une machine déterministe est le modèle formel d'une machine telle que nous les connaissons (nos ordinateurs sont des machines déterministes). Les deux modèles les plus utilisés en informatique théorique sont :

• La machine de Turing
• La machine RAM (Random access machine)

Les machines déterministes font toujours un seul calcul à la fois. Ce calcul est constitué d'étapes élémentaires; à chacune de ces étapes, pour un état donné de la mémoire de la machine, l'action élémentaire effectuée sera toujours la même. Pour la suite, on pourra imaginer sans perte de généralité qu'une machine de Turing déterministe correspond à l'ordinateur favori du lecteur, programmé dans un langage impératif quelconque.

Une machine de Turing non-déterministe est une variante purement théorique des machines de Turing: on ne peut pas construire de telle machine. À chaque étape de son calcul, cette machine peut effectuer un choix non-déterministe: elle a le choix entre plusieurs actions, et elle en effectue une. Si l'un des choix l'amène à accepter l'entrée, on considère qu'elle a fait ce choix-là. En quelque sorte, elle devine toujours juste. Une autre manière de voir leur fonctionnement est de considérer qu'à chaque choix non-déterministe, elles se dédoublent, les clones poursuivent le calcul en parallèle suivant les branches du choix. Si l'un des clones accepte l'entrée, on dit que la machine accepte l'entrée.

Il semblerait donc naturel de penser que les machines de Turing non-déterministes sont beaucoup plus puissantes que les machines de Turing déterministes, autrement dit qu'elles peuvent résoudre en un temps raisonnable des problèmes que les machines ordinaires ne savent pas résoudre à moins de prendre des années.

L'Ordinateur à ADN est un cas particulier de machines non-déterministes, puisqu'il est capable de traiter un calcul en temps constant quelle que soit la taille des données. Notons toutefois que la difficulté est ici transposée en termes de réalisabilité de la machine, qui nécessite des quantités exponentielles d'ADN en fonction de la taille des données.

Complexité en temps et en espace

On désigne par n la taille de la donnée. On peut prendre quelques exemples :

• La donnée d'un graphe à s sommets et n arêtes est de taille  : il y a arêtes possibles dans un tel graphe, et pour chacune, on doit utiliser un bit pour dire si elle est effectivement présente dans le graphe. On peut par exemple choisir une représentation matricielle (il y aura cellules dans la matrice à stocker et chacune vaudra 0 ou 1).
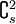
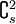
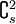
• la taille d'un vecteur d'éléments à trier.

Pour les machines déterministes, on définit la classe TIME(t(n)) des problèmes qui peuvent être résolus en temps t(n). C'est-à-dire pour lesquels il existe au moins un algorithme sur machine déterministe résolvant le problème en temps t(n) (le temps étant le nombre de transitions sur machine de Turing ou le nombre d’opérations sur machine RAM).

• TIME(t(n)) = { L | L peut être décidé en temps t(n) par une machine déterministe }

Pour les machines non déterministes, on définit la classe NTIME(t(n)) des problèmes qui peuvent être résolus en temps t(n).

• NTIME(t(n)) = { L | L peut être décidé en temps t(n) par une machine non-déterministe }

La complexité en espace évalue l'espace mémoire utilisé en fonction de la taille des données ; elle est définie de manière analogue :

• SPACE(s(n)) = { L | L peut être décidé par une machine déterministe en utilisant au plus s(n) cellules de mémoire}
• NSPACE(s(n)) = { L | L peut être décidé par une machine non-déterministe en utilisant au plus s(n) cellules de mémoire}

Le problème du codage

Le codage influence la complexité des problèmes. Il est bon de se rappeler que les données sur lesquelles travaillent les algorithmes sont nécessairement stockées en mémoire (on parle ici de la mémoire de l'ordinateur, mais aussi de la bande de la machine de Turing par exemple).

Si le codage d'une donnée est exponentiel par rapport à la taille de la donnée initiale, l'ensemble des complexités des algorithmes sera sans doute caché par la complexité du codage : il faut par exemple s'interdire de coder le résultat dans l'entrée...

On ne s'intéressera ici qu'aux codages raisonnables.

Problème de décision

Chaque problème informatique peut se réduire à un problème de décision, c’est-à-dire un problème formulé comme une question dont la réponse est Oui ou Non, plutôt que par exemple la taille du plus court chemin est 42. Un problème qui n'est pas formulé de cette manière peut être très simplement transformé en un problème de décision équivalent. Le problème du voyageur de commerce, qui cherche, dans un graphe, à trouver la taille du cycle le plus court passant une fois par chaque sommet, peut s'énoncer en un problème de décision ainsi : Existe-t-il un cycle passant une et une seule fois par chaque sommet tel que la somme des coûts des arcs utilisés soit inférieure à B, avec . Ce problème est équivalent au problème du voyageur de commerce au sens où si l'on sait résoudre efficacement l'un, on sait aussi résoudre efficacement l'autre.

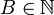
Classes de complexité

La théorie de la complexité repose sur la définition de classes de complexité qui permettent de classer les problèmes en fonction de la complexité des algorithmes qui existent pour les résoudre.

Classe L

Un problème de décision qui peut être résolu par un algorithme déterministe en espace logarithmique par rapport à la taille de l'instance est dans L.

Classe NL

Cette classe s'apparente à la précédente mais pour un algorithme non-déterministe.

Classe P

Un problème de décision est dans P s'il peut être décidé par un algorithme déterministe en un temps polynomial par rapport à la taille de l'instance. On qualifie alors le problème de polynomial.

Prenons par exemple le problème de la connexité dans un graphe. Étant donné un graphe à s sommets, il s'agit de savoir si toutes les paires de sommets sont reliées par un chemin. Pour le résoudre, on dispose de l'algorithme de parcours en profondeur qui va construire un arbre couvrant du graphe à partir d'un sommet. Si cet arbre contient tous les sommets du graphe, alors le graphe est connexe. Le temps nécessaire pour construire cet arbre est au plus s², donc le problème est bien dans la classe P.

Les problèmes dans P correspondent en fait à tous les problèmes facilement solubles.

Classe NP

Un problème NP est Non-déterministe Polynomial (et non pas Non polynomial, erreur très courante).

La classe NP réunit les problèmes de décision pour lesquels la réponse oui peut être décidée par un algorithme non-déterministe en un temps polynomial par rapport à la taille de l'instance.

De façon équivalente, c'est la classe des problèmes qui admettent un algorithme dans P qui, étant donné une solution du problème NP (un certificat), est capable de répondre oui ou non.

Intuitivement, les problèmes dans NP sont tous les problèmes qui peuvent être résolus en énumérant l'ensemble des solutions possibles et en les testant avec un algorithme polynomial.

Par exemple, la recherche de cycle hamiltonien dans un graphe peut se faire avec deux algorithmes :

• le premier génère l'ensemble des cycles (ce qui est exponentiel) ;
• le second teste les solutions (en temps polynomial).

Classe Co-NP (Complémentaire de NP)

C'est le nom parfois donné pour l'équivalent de la classe NP, mais avec la réponse non.

Classe PSPACE

Elle regroupe les problèmes décidables par un algorithme déterministe en espace polynomial par rapport à la taille de son instance.

Classe NSPACE ou NPSPACE

Elle réunit les problèmes décidables par un algorithme non-déterministe en espace polynomial par rapport à la taille de son instance.

Classe LOGSPACE

Classe EXPTIME

Elle rassemble les problèmes décidables par un algorithme déterministe en temps exponentiel par rapport à la taille de son instance.

Propriétés

On a les inclusions :

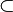
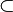
• P NP, et symétriquement P Co-NP
• NP PSPACE = NPSPACE, et Co-NP PSPACE.

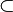
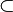
En effet, un problème polynomial peut se résoudre en générant une solution et en la testant avec un algorithme polynomial. Tout problème dans P est aussi dans NP.

La recherche travaille activement à déterminer si NP P (concluant à P = NP) ou si, au contraire P NP (voir le problème ouvert P = NP).

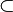
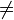
Problème C-Complet

Soit C une classe de complexité (comme P, NP, etc.). On dit qu'un problème est C-complet si

• il est dans C, et
• il est C-difficile (on utilise parfois la traduction incorrecte C-dur).

Un problème est C-difficile si ce problème est au moins aussi dur que tous les problèmes dans C. Formellement on définit une notion de réduction : Soient Π et Π' deux problèmes ; Une réduction de Π' à Π est un algorithme transformant toute instance de Π' en une instance de Π. Ainsi, si l'on a un algorithme pour résoudre Π, on sait aussi résoudre Π'. Π est donc au moins aussi difficile à résoudre que Π'.

Π est alors C-difficile si pour tout problème Π' de C, Π' se réduit à Π. Quand on parle de problèmes NP-difficiles on s'autorise uniquement des réductions dans P, c'est-à-dire que l'algorithme qui calcule le passage d'une instance de Π' à une instance de Π est polynomial (voir Réduction polynomiale). Quand on parle de problèmes P-difficiles on s'autorise uniquement des réductions dans LOGSPACE.

Réduction de problèmes

Pour montrer qu'un problème Π est C-difficile pour une classe C donnée, il y a deux façons de procéder: montrer que tout problème de C se réduit à Π, ou bien il suffit de montrer qu’un problème C-difficile se réduit à Π. C'est cette deuxième méthode, plus facile, qui est utilisée dès que l'on dispose d'au moins un problème C-complet.

Transformation de problème

La réduction la plus simple (ce n'est d'ailleurs pas vraiment une réduction) consiste simplement à transformer le problème à classer en un problème déjà classé.

Par exemple, démontrons ici que le problème de la recherche de cycle hamiltonien dans un graphe orienté est NP-Complet.

• Le problème est dans NP : On peut trouver de façon évidente un algorithme pour le résoudre avec une machine non-déterministe, par exemple en énonçant tous les cycles puis en sélectionnant le plus court.
• Nous disposons du problème de la recherche de cycle hamiltonien pour les graphes non-orientés. Un graphe non-orienté peut se transformer en un graphe orienté en " doublant " chaque arête de manière à obtenir, pour chaque paire de nœuds adjacents, des chemins dans les deux sens. Il est donc possible de ramener le problème connu, NP-difficile, au problème que nous voulons classer. Le nouveau problème est donc NP-difficile.

Le problème étant dans NP et NP-difficile, il est NP-complet.

Réduction polynomiale

Voir l'article complet réduction polynomiale.

Théorème de Cook

Les problèmes sont classés de façon incrémentale, la classe d'un nouveau problème étant déduite de la classe d'un ancien problème.

L'établissement d'un " premier " problème NP-complet pour classer tous les autres s'est toutefois avéré nécessaire : Ainsi le théorème de Cook (de Stephen Cook) classe le problème SAT comme NP-Complet.

Problème NP-Complet

Les problèmes complets les plus étudiés sont les problèmes NP-complets. La classe de complexité étant par définition réservée à des problèmes de décisions, on parlera de problème NP-difficile pour les problèmes d'optimisation sachant que - pour ces problèmes d'optimisation - on peut construire facilement un problème qui lui est associé et est dans NP et qui est donc NP-complet.

De manière intuitive, dire qu'un problème peut être décidé à l'aide d'un algorithme non-déterministe polynomial signifie qu'il est facile, pour une solution donnée, de vérifier en un temps polynomial si celle-ci répond au problème pour une instance donnée (à l'aide d'un certificat); mais que le nombre de solutions à tester pour résoudre le problème est exponentiel par rapport à la taille de l'instance.

Le non-déterminisme permet de masquer la taille exponentielle des solutions à tester tout en permettant à l'algorithme de rester polynomial.

Problème NP-Complets célèbres 

• Problème SAT et variante 3SAT (mais 2SAT est polynomial) ; notons qu'il existe des logiciels (dits SAT solvers) spécialisés dans la résolution performante de problèmes SAT ;
• Problème du voyageur de commerce
• Problème du cycle hamiltonien
• Problème de la clique maximum
• Problèmes de colorations de graphes
• Problème d'ensemble dominant dans un graphe
• Problème de couverture de sommets dans un graphe

Bien que moins étudiés, les problèmes complets pour les autres classes ne sont pas moins intéressants

• Le problème Reach (ou Accessibilité) qui consiste à savoir s’il existe un chemin entre deux sommets d'un graphe est NL-complet
• Le problème Circuit Value (et monotone Circuit Value : le même mais sans négation) sont des problèmes P-complets
• Le problème QBF (SAT avec des quantificateurs) est PSPACE-complet

Remarque : tous les problèmes de la classe L sont L-complets vu que la notion de réduction est trop vague. En effet la fonction qui doit transformer un instance d'un problème à l'autre doit se calculer en espace logarithmique.

Listes

• 21 problèmes NP-complets de Karp
• Liste de problèmes NP-complets

Le problème ouvert P=NP

On a trivialement car un algorithme déterministe est un algorithme non déterministe particulier. En revanche la réciproque : , que l'on résume généralement à P = NP du fait de la trivialité de l'autre inclusion, est l'un des problèmes ouverts les plus fondamentaux et intéressants en informatique théorique. Cette question a été posée en 1970 pour la première fois ; celui qui arrivera à décider si P et NP sont différents ou égaux recevra le prix Clay (plus de 1 000 000 $).

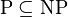
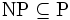
Le problème P = NP revient à savoir si on peut résoudre un problème NP-Complet avec un algorithme polynomial. Les problèmes étant tous classés les uns à partir des autres — un problème est NP-Complet si l'on peut réduire un problème NP-Complet connu en ce problème —, faire tomber un seul de ces problèmes dans la classe P fait tomber l'ensemble de la classe NP, ces problèmes étant massivement utilisés, en raison de leur difficulté, par l'industrie, notamment en cryptographie — cf. la factorisation en nombres premiers). Ceci fait qu'on conjecture cependant que les problèmes NP-complets ne sont pas solubles en un temps polynomial. À partir de là plusieurs approches sont tentées :

• Des algorithmes d'approximation permettent de trouver des solutions approchées de l'optimum en un temps raisonnable pour un certain nombre de programmes. Dans le cas d'un problème d'optimisation on trouve généralement une réponse correcte, sans savoir s'il s'agit de la meilleure solution ;
• Des algorithmes stochastiques : en utilisant des nombres aléatoires on peut "forcer" un algorithme à ne pas utiliser les cas les moins favorables, l'utilisateur devant préciser une probabilité maximale admise que l'algorithme fournisse un résultat erroné. Citons notamment comme application des algorithmes de test de primalité en temps polynomial en la taille du nombre à tester. A noter qu'un algorithme polynomial non stochastique a été proposé pour ce problème en août 2002 par Agrawal, Kayal et Saxena ;
• Des heuristiques permettent d'obtenir des solutions généralement bonnes mais non exactes en un temps de calcul modéré ;
• Des algorithmes par séparation et évaluation permettent de trouver la ou les solutions exactes. Le temps de calcul n'est bien sûr pas borné polynomialement mais, pour certaines classes de problèmes, il peut rester modéré pour des instances relativement grandes ;
• On peut restreindre la classe des problèmes d'entrée à une sous-classe suffisante, mais plus facile à résoudre.

Si ces approches échouent, le problème est non soluble en pratique dans l'état actuel des connaissances.

Pour le cas de L et NL, on ne sait pas non plus si L = NL. Mais cette question est moins primordiale car . De fait, les problèmes dans L et dans NL sont solubles efficacement.

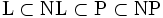
Inversement on sait que PSPACE = NPSPACE. Par contre . Donc, avant de résoudre NP = PSPACE, il faut résoudre P = NP.

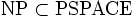
Pour résumer, on a . On sait de plus que NL est strictement inclus dans PSPACE. Donc deux classes au moins entre NL et PSPACE ne sont pas égales.

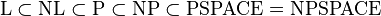
Modèles de calcul

Ces théorèmes ont été établis grâce au modèle des machines de Turing. Mais d'autres modèles sont utilisés en complexité, dont :

• les fonctions récursives dues à Kleene
• les automates cellulaires
• les machines à registres (RAM)
• le lambda-calcul

On sait que tous ces modèles sont équivalents : tout ce qu'un modèle permet de calculer est calculable par un autre modèle. De plus, grâce aux machines universelles de Turing, on sait que tout ce qui est intuitivement calculable est modélisable dans ces systèmes. Les conséquences sont importantes et nombreuses. La première fait que cet article est lisible : on peut construire des ordinateurs. Ceci fait un lien avec la théorie de la calculabilité.