Système T - Définition

A l'instar de la récursion primitive ou le lambda-calcul, le Système T est un langage de programmation théorique. Il a été inventé par le logicien Kurt Gödel.

Ce système consiste en une fusion de la récursion primitive et du lambda-calcul simplement typé. Le but est d'augmenter le pouvoir expressif et c'est gagné car on peut programmer facilement la fonction d'Ackermann.

Le principe est simple : on garde les schémas récursifs primitifs :

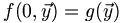
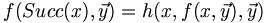
La différence majeure c'est que l'on autorise les paramètres à être des fonctions. Ceci change tout car par rapport à la récursion primitive on va pouvoir faire une récurrence sur plusieurs paramètres et c'est exactement ce qu'il manquait.

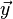
Formalisme

Selon le formalisme de Martin-Löf on peut écrire les termes du système T par récurrence

• 0 : de type N
• si t est un terme de type N alors S(t) est un terme de type N
• les variables x, y, z, ... de type T sont des termes de type T
• si x est une variable de type U et t un terme de type V alors λx.t est un terme de type U→V
• si t est un terme de type U→V et u un terme de type U alors tu est un terme de type V
• si t un terme de type N et que b et s sont des termes de type T alors rec_T(t,b,(x^N,y^T)s) est un terme de type T

Pour comprendre comment fonctionne ce système il faut naturellement des règles de réduction.

• (λx.t)u → t[x←u]
• rec_T(0,b,(x^N,y^T)s) → b
• rec_T(S(t),b,(x^N,y^T)s) → s[x←t, y←rec_T(t,b,(x^N,y^T)s)

On garde les notions de substitution du lambda-calcul et de la récursion primitive, ainsi que les " règles additionnelles " qui permettent de réduire " à l'intérieur " d'un terme.

Quelques théorèmes importants

• tous les termes clos (sans variables libres) de type N sont des numéraux (un Sⁿ(0))
• tous les termes clos de type N sont normalisables

Exemples

La fonction d'Ackermann

Notre fameuse fonction d'Ackermann que l'on ne peut pas programmer en récursion primitive est définie par les équations suivantes :

• Ack 0 p = S(p)
• Ack S(n) 0 = Ack n S(0)
• Ack S(n) S(p) = Ack n (Ack S(n) p)

Ces équations n'ont pas la forme voulue mais en modifiant un peu on obtient la forme désirée :

• Ack 0 = λp.S(p)
• Ack S(n) = λp.Ack' p (Ack n)
• Ack' 0 f = f S(0)
• Ack' S(p) f = f (Ack' p f)

Il n'y a plus qu'à écrire cela sous forme de terme :

Ack = λn.rec_N→N(n, λp.S(p), (m^N, f^N→N)λp.rec_N(p, f S(0), (q^N, g^N)f g)))

Un minimum efficace

En récursion primitive on ne peut pas faire une fonction qui retourne le minimum de deux entiers en temps de calcul minimum de ces deux entiers. C'est très contraignant par exemple si on calcule le minimum de 2 et 1 000 000. Comme avec le système T on peut s'arranger pour faire des récursions sur plusieurs paramètres, ne nous gênons pas.

Equations intuitives :

• Min 0 p = 0
• Min S(n) 0 = 0
• Min S(n) S(p) = S(Min n p)

En transformant un peu on obtient des équations utilisant le schéma souhaité :

• Min 0 = λp.0
• Min S(n) = λp.Min' p (Min n)
• Min' 0 f = 0
• Min' S(p) f = S(f p)

Le terme voulu est :

Min = λn.rec_N→N(n, λp.0, (m^N, f^N→N)λp.rec_N( p, 0, (q^N, g^N) S(f q))))

De la même manière on peut obtenir facilement un programme optimisé pour l'addition et la soustraction.