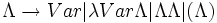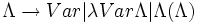Lambda-calcul - Définition

Le lambda-calcul (ou λ-calcul) est un langage de programmation théorique inventé par Alonzo Church dans les années 1930. Ce langage a été le premier utilisé pour définir et caractériser les fonctions récursives et il a eu une grande importance dans la théorie de la calculabilité à l'égal des machines de Turing et du modèle de Herbrand-Gödel. Il s'agit d'un modèle de calcul, c’est-à-dire une formalisation de la notion de calcul. Or on peut simuler la normalisation des λ-termes à l'aide d'une machine de Turing, et simuler une machine de Turing par des λ-termes. Ces deux modèles sont donc équivalents (ou Turing-équivalents). Or la thèse de Church-Turing dit que tout algorithme peut être calculé par le lambda-calcul, donc par l'équivalence que tout algorithme peut être calculé par une machine de Turing. C'est ainsi que le premier langage de programmation est né.

Les lambda calculs typés sont à l'origine des langages de programmation fonctionnels comme Lisp ou Caml car la théorie des types apporte une sémantique forte et sûre.

Le lambda-calcul est apparenté à la logique combinatoire due à Haskell Curry.

Syntaxe

Les objets du lambda-calcul sont les lambda-termes. Il en existe trois sortes :

• les variables : x, y, ...
• les applications : si u et v sont des lambda-termes uv est aussi un lambda-terme. On peut alors voir u comme une fonction et v comme un argument, uv étant alors l'image de v par la fonction u.
• les abstractions : si x est une variable et u un lambda-terme alors λx.u est un lambda-terme. Intuitivement, λx.u est la fonction qui à x associe u.

Pour des raisons pratiques, on introduit parfois également des constantes et des opérations primitives (par exemple les entiers naturels et les opérations + et * usuelles). Ainsi, la fonction qui, à x associe x + 2 pourra être représentée par λx.x + 2. Du point de vue du lambda calcul " pur ", ces primitives se comportent comme des variables, si ce n'est qu'on peut leur donner des règles de calcul spéciales (cf. ci-dessous).

Notations

Arguments/Abstraction multiples

Vous aurez remarqué qu'un lambda ne prend qu'un seul argument mais on peut contourner cet obstacle de la façon suivante : la fonction qui au couple (x, y) associe u sera considérée comme une fonction qui, à x, associe une fonction qui, à y, associe u. Elle est donc notée : λx.(λy.u). Au point de vue de la notation on peut aussi écrire λx.λy.u ou λxλy.u ou tout simplement λxy.u. Par exemple, la fonction qui, au couple (x, y) associe x + y pourra être notée λx.λy.x + y ou plus simplement λxy.x + y.

Parenthésage

Du point de vue du parenthésage x₁ x₂ ... x_n = ((x₁ x₂) ... x_n)

Pour le parenthésage, il y a plusieurs formalismes:

1. 

Comme expliqué ci-dessus, un parenthésage à gauche. (On conviendra d'utiliser cette convention ici)

1. 

Qui correspond à un parenthésage à droite.

Contraction

On peut contracter certaines parties d'un lambda-terme : plusieurs applications successives d'un même terme/variable peuvent etre " factorisées ".

λx.ffffx est équivalent à : λx.f⁴x

Variables libres

Dans les expressions mathématiques il y a deux types de variables : les variables libres et les variables liées (ou muettes). Les variables liées sont locales à un morceau de l'expression. On peut les renommer à volonté sans changer la signification de l'expression.

Par exemple dans , x est libre, mais y est liée (par le dy). Ceci est la même expression que car y était un nom local, tout comme l'est z. Par contre ne correspond pas à la même expression car le x est libre. D'ailleurs la notation f(x) précise que l'ensemble de ses variables (libres) est {x}.

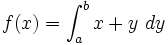
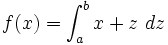
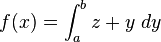
Tout comme l'intégrale lie la variable d'intégration, le λ lie la variable qui le suit.

Exemples: dans λx.xy x est lié, et y libre. On peut réecrire ce terme ainsi : λt.ty.

Plus compliqué λxyzt.z(xt)ab(zsy) est aussi équivalent à λwjit.i(wt)ab(isj)

On définit l'ensemble VL(t) des variables libres d'un terme t par récurrence :

• si x est une variable alors VL(x) = {x}
• si u et v sont des lambda-termes alors VL(u v) = VL(u) ∪ VL(v)
• si x est une variable et u un lambda-terme alors VL(λx.u) = VL(u) - {x}

Si un lambda-terme n'a pas de variables libres alors on dit qu'il est clos.

Principes

L'outil le plus important pour le calcul est la substitution. Cette opération permet de remplacer une variable par un terme. Grâce à ce mécanisme, les réductions vont pouvoir " calculer " le terme.

La substitution dans un lambda terme t d'une variable x par un terme u est notée t[x := u]. On la définit par récurrence sur t :

• si t est une variable alors t[x := u]=u si x=t et t sinon
• si t = v w alors t[x := u] = v[x := u] w[x := u]
• si t = λy.v alors t[x := u] = λy.(v[x := u]) si xy et t sinon

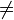
Dans le dernier cas on fera attention à ce que y ne soit pas une variable libre de u. En effet, elle serait alors " capturée " par le lambda externe. Si c'est le cas on renomme y et toutes ses occurrences dans v. C'est l'alpha-conversion, qui permet d'identifier λy.v et λz.v[y := z]. Rappelez vous que les variables sous les lambdas sont des variables dites " muettes ".

Exemples :

• λx.xy[y := a] = λx.xa
• λx.xy[y := x] = λz.zx(et non λ x.xx, qui est totalement différent)

Remarque : l'alpha-conversion, qui permet d'identifier λy.v et λz.v[y := z] doit être définie avec précaution et avant la substitution. En effet la substitution de z dans v n'est pas encore disponible et pose les mêmes problèmes de capture. Ainsi dans le terme λx.λy.xyλz.z, on ne pourra pas renommer x en y (on obtiendrait λy.λy.yyλz.z) par contre on peut renommer x en z.

Les définitions formelles et correctes de la alpha-conversion et de la substitution se trouvent dans le livre de J.-L. Krivine par exemple, mais une bonne compréhension de la notion de variables liées, habituelles en mathématiques, suffit largement pour comprendre le lambda-calcul.

Définie ainsi la substitution est un mécanisme externe au lambda-calcul, on dit aussi qu'il fait partie de la méta-théorie. A noter que certains travaux visent à introduire la substitution comme un mécanisme interne au lambda-calcul, conduisant à ce qu'on appelle les calculs de substitutions explicites.

Réductions

Les termes sont des arbres avec des nœuds binaires (applications), des nœuds unaires (les λ-abstractions) et des feuilles (les variables). Les réductions permettent de modifier l'arbre, cependant l'arbre n'est pas forcément " plus petit " après l'opération. Exemple : si vous réduisez (λx.xxx)(λx.xxx) vous obtiendrez (λx.xxx)(λx.xxx)(λx.xxx). La réduction tient son nom du fait que l'on va réduire un morceau du terme : le rédex.

On appelle rédex un terme de la forme (λx.u) v. On définit alors la bêta-contraction (ou réduction) de (λx.u) v comme u[x := v]; on note → la relation de réduction: ainsi (λx.u) v donne u[x := v]. Intuitivement, (λx.u)v est la valeur de la fonction λx.u appliquée à la variable v. u étant l'image de x par la fonction (λx.u), l'image de v est obtenue en substituant dans u, x par v. Inversement u[x := v] est appelé le contractum de (λx.u) v.

Exemple de réduction :

(λx.xy)a donne xy[x := a] = ay

On note →^* la fermeture réflexive transitive de la relation → de contraction (→^* est appelée la bêta-réduction) et =_β sa fermeture réflexive symétrique et transitive (appelée bêta-conversion ou bêta-equivalence).

La β-conversion permet de faire une "marche arrière" à partir d'un terme. Cela permet, par exemple, de retrouver le terme avant une β-réduction. Passer de x à (λy.y)x.

On peut écrire

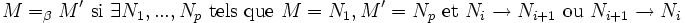
On va ainsi voyager par des réductions, et par des retours en arrière de M à M'.

On utilise également assez fréquemment une autre opération, appelée êta-réduction (ou son inverse la êta-expansion), définie ainsi : λx.ux →_η u, lorsque x n'apparaît pas libre dans u. En effet, ux s'interprête comme l'image de x par la fonction u. λx.ux s'interprête alors comme la fonction qui, à x, associe l'image de x par u, donc comme la fonction u elle-même.

Enfin, si on s'est donné des primitives, on peut fixer leur comportement calculatoire au moyen des règles de delta-réduction. Par exemple, si on s'est donné les entiers et + comme termes supplémentaires, les tables d'addition serviront de delta-règles. Comme les primitives sont par définition complètement étrangères au lambda-calcul, leurs règles de calcul peuvent a priori adopter n'importe quelle forme. Toutefois, si on veut étendre les propriétés mentionnées ci-dessous au cas d'un calcul avec des primitives, on est amené à faire quelques hypothèses sur les règles ajoutées.

La normalisation : notion de calcul

Le calcul d'un lambda-terme peut être défini par sa réduction. Sa forme originale est l'énoncé et la forme normale est le résultat.

Un lambda-terme t est dit en forme normale si aucune bêta-contraction ne peut lui être appliquée, c'est-à-dire si t ne contient aucun rédex. Ou encore, s'il n'existe aucun lambda-terme u tel que t → u.

Exemple: λx.y(λz.z(yz))

On dit qu'un lambda-terme t est normalisable s'il existe une forme normale u et une suite de lambda-termes t₁, ..., t_n telle que t = t₁, u = t_n et pour tout i (1 ≤ i < n) t_i → t_i+1 ou t_i+1 → t_i. Un tel u est appelé la forme normale de t.

On dit qu'un lambda terme t est fortement normalisable si toutes les réductions à partir de t sont finies.

Exemples:

1. Voici l'exemple le plus classique de lambda-terme non fortement normalisable :
   Ω = (λx.xx)(λx.xx) = ΔΔ
   Le lambda terme Ω n'est pas fortement normalisable car il boucle infiniment sur lui-même si on tente de le réduire.
   . ((λx.xx) s'applique sur le premier argument de (λx.xx), les deux x suivant le point prennent donc cette valeur, et on retrouve le terme de départ.)
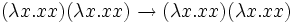
2. (λx.x)((λy.y)z) est un lambda-terme fortement normalisable.
3. (λx.y)(ΔΔ) est normalisable, mais pas fortement normalisable.

Si un terme est fortement normalisable, alors il est normalisable.

Théorème de Church-Rosser : soient t et u deux termes tels que t =_β u. Il existe un terme v tel que t →^* v et u →^* v.

Théorème du losange (ou de confluence) : soient t, u₁ et u₂ des lambda-termes tels que t →^* u₁ et t →^* u₂. Alors il existe un lambda-terme v tel que u₁ →^* v et u₂ →^* v.

Grâce au Théorème de Church-Rosser on peut facilement montrer l'unicité de la forme normale ainsi que la cohérence du lambda-calcul (c’est-à-dire qu'il existe au moins deux termes distincts non bêta-convertibles).

Différents Lambda-calculs

Le lambda-calcul défini ci-dessus n'est qu'une trame syntaxique appelée à être complétée par une sémantique qui permet de donner une signification à ce que l'on fait par ce lambda-calcul. On peut distinguer deux grandes classes de lambda-calculs : les lambda-calculs non typés et les lambda-calculs typés. La différence est qu'avec les types on va restreindre les termes valides. C’est-à-dire que généralement on va chercher à enlever les termes qui ne sont pas normalisables. Le but est d'avoir un lambda-calcul qui vérfie les propriétés de Church-Rosser et de normalisation (voire normalisation forte).

Même si en restreignant les termes valides par les types on garde généralement les plus intéressants. De plus grâce à l'isomorphisme de Curry-Howard on peut relier un lambda calcul à une logique et par là un terme correspond à une preuve. Intuitivement c'est très fort parce que cela permet d'associer à une preuve mathématique un programme informatique. C'est sur cela que se base une partie des prouveurs automatiques et semi-automatiques.

Le Lambda-calcul non typé

On va utiliser des codages pour créer les objets usuels de l'informatique. Grâce à ces objets on peut tout calculer car on peut simuler une machine de Turing. Et grâce aux théorèmes de la théorie de la calculabilité on en déduit que le lambda-calcul est un modèle universel de calcul.

Les booléens

Pour faire de vrais calculs on va faire des codages. On définit le booléen vrai par λab.a et faux par λab.b

Nous remarquons que :

vrai x y →^* x

et que :

faux x y →^* y

Nous en déduisons un programme pour ifthenelse : λbuv.buv

On pourra vérifier que :

ifthenelse vrai x y →^* x

et que :

ifthenelse faux x y →^* y

À partir de là nous avons aussi un lambda-terme pour les opérations booléennes classiques :

non = λb.ifthenelse b faux vrai

et = λab.ifthenelse a b faux ou bien λab.ifthenelse a b a

ou = λab.ifthenelse a vrai b ou bien λab.ifthenelse a a b

Les entiers

Nous allons utiliser les Entiers de Church. n = λfx.f(f(...(f x)...)) = λfx.fⁿx avec n f. Par exemple 0 = λfx.x, 3 = λfx.f(f(f x)).

Quelques fonctions

Il y a deux manières de coder la fonction successeur. Soit en ajoutant un f en tête soit en queue. Au départ nous avons n = λfx.fⁿ x et nous voulons λfx.fⁿ⁺¹ x. Il faut pouvoir rajouter un f soit au début des f " sous " les lambdas soit à la fin.

• Si nous choisissons de le mettre en tête, il faut pouvoir entrer " sous " les lambdas. Pour cela il faut créer des redex donc si n est notre entier il faut faire n f x, ce qui donne fⁿ x. En mettant un f en tête nous avons presque terminé : f (n f x) → f(fⁿ x) = fⁿ⁺¹ x. Il nous faut maintenant refaire les lambdas pour reconstruire un entier de Church : λfx.f (n f x) = λfx.fⁿ⁺¹ x (nous aurions bien sûr pu prendre d'autres noms de variables que f et x à l'étape précédente et donc nous aurions gardé ces noms ici). Enfin pour avoir la " fonction " successeur il faut bien entendu prendre un entier en paramètre, donc rajouter un lambda. Nous obtenons λnfx.f(n f x). Le lecteur pourra vérifier que (λnfx.f(n f x)) 3 = 4, avec 3 = λfx.f(f(f x))) et 4 = λfx.f(f(f(f x)))).
• Si par contre nous voulions mettre le f en queue, c'est légèrement plus rusé. Lorsque nous avons " décortiqué " l'entier pour enlever les lambdas, nous avons appliqué des simples variables à nos lambdas. Rien ne nous empêche de mettre autre chose. Or ici nous voulons bien f x à la place de x : nous allons donc faire ceci : n f (f x), ce qui se réduit à fⁿ (f x) = fⁿ⁺¹ x. On n'a plus qu'à refaire l'emballage comme dans le cas précédent et on obtient λnfx.n f (f x). La même vérification pourra être faite.

Les autres fonctions sont construites avec le même principe, en appliquant ce qu'il faut dans f et x. Par exemple l'addition en " concaténant " les deux lambda-termes : λnpfx.n f (p f x).

Pour coder la multiplication c'est un peu plus futé : on va utiliser le f pour " propager " une fonction sur tout le terme : λnpfx.(n (p f) x)

L'exponentielle n'est pas triviale contrairement à ce que son écriture laisse penser, et lors de la réduction on est obligé de renommer les variables : λnp.p n

Le prédécesseur et la soustraction ne sont pas simples non plus. On en reparlera plus loin.

On peut définir le test à 0 ainsi : if0thenelse = λnab.n (λx.b) a, ou bien en utilisant les booléens λn.n (λx.faux) vrai.

Les itérateurs

Tout cela n'est pas très intuitif alors pour pouvoir coder des algorithmes on définit la fonction d'itération sur les entiers : iterate = λnuv.n u v

Le truc c'est que v est le cas de base et u une fonction sur le cas de récurrence.

Par exemple l'addition qui provient de ces équations

• add(0, p) = p
• add(n+1, p) = (n+p) + 1

On va donc programmer par itération avec le successeur sur le cas de base p. Le lambda-terme est donc λnp.iterate n successeur p. On remarquera que add n p →^* n successeur p.

Les couples

On peut coder des couples par c = λz.z a b où a est le premier élément et b le deuxième. On notera ce couple (a,b). Pour accéder aux deux parties on utilise π₁ = λc.c (λab.a) et π₂ = λc.c (λab.b). On reconnaîtra les booléens vrai et faux dans ces expressions et on laissera le soin au lecteur de réduire π₁(λz.z a b)

Les listes

On peut remarquer qu'un entier est une liste qui ne contient pas de clé. En rajoutant une information on peut construire les listes d'une manière analogue aux entiers : [a₁ ; ... ; a_n] = λgy. g a₁ (... (g a_n y)...)

Les itérateurs sur les listes

De la même manière qu'on a introduit une itération sur les entiers on introduit une itération sur les listes. la fonction liste_it se définit par λlxm.l x m comme pour les entiers. Le concept est à peu près le même mais il y a des petites nuances. Nous allons voir par un exemple.

exemple : La longueur d'une liste est définie par

• longueur ((lien)) = 0
• longueur (x :: l) = 1 + longueur l

x :: l est la liste de tête x et de queue l (notation ML). Cela se code par λl.liste_it l (λym.add (λfx.f x) m) (λfx.x) ou tout simplement λl.l (λym.add 1 m) 0

Les arbres binaires

Le principe de construction des entiers, des couples et des listes se généralise aux arbres binaires :

• constructeur de feuille : feuille = λngy.y n
• constructeur de nœud : nœud = λbcgy.g (b g y) (c g y) (avec b et c des arbres binaires)
• itérateur : arbre_it = λaxm.a x m

Un arbre est soit une feuille, soit un nœud. Dans ce modèle, aucune information n'est stockée au niveau des nœuds, les données (ou clés) sont conservées au niveau des feuilles uniquement. On peut alors définir la fonction qui calcule le nombre de feuilles d'un arbre : nb_feuilles = λa.arbre_it a (λbc.add b c) (λn.1), ou plus simplement: nb_feuilles = λa.a add (λn.1)

Le prédécesseur

Pour définir le prédécesseur avec les entiers de Church, il faut ruser et utiliser les couples. L'idée est de reconstruire le prédécesseur par itération : pred = λn.π₁ (iterate n (λc.(π₂ c,successeur (π₂ c))) (0,0)). On note en passant que le prédécesseur sur les entiers naturels n'est pas spécialement défini en 0. On a ici arbitrairement adopté la convention qu'il vaudrait 0.

On vérifie par exemple que pred 3 →^* π₁ (iterate 3 (λc.(π₂ c,successeur (π₂ c))) (0,0)) →^* π₁ (2,3) →^* 2.

On en déduit que la soustraction est définissable par : sub = λnp.iterate p pred n avec la convention que si p est plus grand que n, alors sub n p vaut 0.

La récursion

En combinant prédécesseur et itérateur, on obtient un récurseur. Celui-ci se distingue de l'itérateur par le fait que la fonction qui est passée en argument a accès au prédécesseur.

rec = λnfx.π₁ (n (λc.(f (π₂ c) (π₁ c),successeur (π₂ c))) (x,0))

Le combinateur de point fixe

Le combinateur de point fixe permet de faire des boucles infinies. Ceci est pratique pour programmer des fonctions qui ne s'expriment pas simplement par itération, telle que le pgcd, et c'est surtout nécessaire pour programmer des fonctions partielles.

Le combinateur de point de fixe le plus simple est : Y = λf.(λx.f(x x))(λx.f(x x))

On vérifie que quelque soit g. Grâce au combinateur de point de fixe, on peut par exemple définir une fonction qui prend en argument une fonction et teste si cette fonction argument renvoie vrai pour au moins un entier: teste_annulation = λg.Y (λfn.ou (g n) (f (successeur n))) 0.

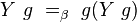
Par exemple, si on définit la suite alternée des booléens vrai et faux : alternate = λn.iterate n non faux, alors, on vérifie que : teste_annulation alternate →^* ou (alternate 0) (Y (λfn.ou (alternate n) (f successeur n)) (successeur 0)) →^* ou (alternate 1) (Y (λfn.ou (alternate n) (f successeur n)) (successeur 1)) →^* vrai.

On peut aussi définir le pgcd : pgcd = Y (λfnp.if0thenelse (sub p n) (if0thenelse (sub n p) p (f p (sub n p))) (f n (sub p n))).

Connexion avec les fonctions partielles récursives

Le récurseur et le point fixe sont des ingrédients clés permettant de montrer que toute fonction partielle récursive est définissable en λ-calcul lorsque les entiers sont interprétés par les entiers de Church. Réciproquement, les λ-termes peuvent être codés par des entiers et la réduction des λ-termes est définissable comme une fonction (partielle) récursive. Le λ-calcul est donc un modèle de la calculabilité

Le Lambda-calcul simplement typé

On introduit des types simples sur les termes, et on n'accepte que les termes bien typés. Outre un souci de clarté et de compréhension, cela permet d'avoir la normalisation forte, c'est-à-dire que pour tous les termes, toutes les réductions aboutissent à une forme normale (qui est unique pour chaque terme de départ). Autrement dit, tous les calculs menés dans ce contexte terminent. En contrepartie, le pouvoir expressif de ce calcul est très limité (ainsi, l'exponentielle ne peut y être définie, ni même la fonction ).

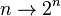
Plus formellement, les types sont construit de la manière suivante:

• un type de base ι (si on a des primitives, on peut aussi se donner plusieurs types de bases, comme les entiers, les booléens, les caractères, etc. mais cela n'a pas d'incidence au niveau de la théorie).
• si τ₁ et τ₂ sont des types, est un type.

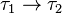
Intuitivement, le second cas représente le type des fonctions acceptant un élément de type τ₁ et renvoyant un élément de type τ₂.

Un contexte Γ est un ensemble de paires de la forme (x,τ) où x est une variable et τ un type. Un jugement de typage est un triplet (on dit alors que t est bien typé dans Γ), défini récursivement par:

• si , alors .
• si , alors .
• si et , alors

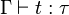
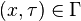
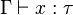
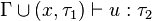
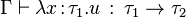
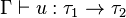
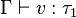
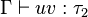
Si on s'est donné des primitives, il faut leur donner un type (via Γ). Dans le cas de la règle de l'abstraction, l'ajout de x masque une éventuelle occurrence précédente de la variable dans Γ.

Les Lambda-calculs typés d'ordres supérieurs

Le lambda-calcul simplement typé est trop restrictif pour pouvoir calculer toutes les fonctions dont on a besoin habituellement en mathématiques et donc dans un programme informatique. Un autre modèle permet de calculer toutes les fonctions calculables dans un temps plus ou moins acceptable : la récursion primitive. Ce système permet de calculer la plupart des fonctions calculables par une machine de Turing. Le problème est au niveau de la complexité car on n'a pas de bons algorithmes de calcul et donc de manière efficace de calculer. Ce problème est réglé avec le Système T de Gödel qui fusionne la récursion primitive et le lambda-calcul simplement typé. Dans ce système on n'a pas seulement de nouveaux algorithmes mais aussi de nouveaux programmes comme la fameuse fonction d'Ackermann qui est la plus petite fonction non primitive récursive. Cependant elle est hors de portée des ordinateurs actuels car on n'aurait même pas assez de mémoire pour stocker le résultat de la fonction appliquée aux arguments 5 5 par exemple.

Bien que ce modèle permette de calculer tout ce que l'on veut avec des algorithmes corrects, théoriquement on peut faire beaucoup mieux. Notamment par l'introduction des variables de type. Cela augmente la complexité (du point de vue compréhension et non informatique) du système mais augmente considérablement le pouvoir expressif. Pour les lambdas calculs typés du second ordre on peut faire des termes qui dépendent de types, des types qui dépendent de termes et des types qui dépendent de types. En faisant la combinaison de chacun on obtient huit lambda-calculs que Barendregt modélise sous forme de cube. L'extrémité du cube opposée à celle du lambda-calcul simplement typé est le calcul des constructions dû à Thierry Coquand, et a donné naissance au système coq.

Bibliographie

• (en) Henk Barendregt, The Lambda-Calculus, volume 103, Elsevier Science Publishing Company, Amsterdam, 1984.
• Jean-Louis Krivine, Lambda-Calcul, types et modèles, Masson 1991.
• (en) Steven Fortune, Daniel Leivant, Michael O'Donnell, " The Expressiveness of Simple and Second-Order Type Structures " dans Journal of the ACM vol. 30 (1983), p. 151-185.
• (en) Jean-Yves Girard, Paul Taylor, Yves Lafont, Proofs and Types, Cambridge University Press, New York, 1989 (ISBN 0-521-37181-3).
• Hervé Poirier, " La Vraie Nature de l'intelligence ", dans Science et Vie n^o 1013 (février 2002), p. 38-57.
• Francis Renaud, Sémantique du temps et lambda-calcul, Presses Universitaires de France, 1996 (ISBN 2-13-047709 7)