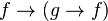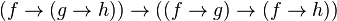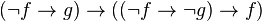Calcul des prédicats - Définition
Le calcul des prédicats du premier ordre, ou calcul des relations, ou logique du premier ordre, ou tout simplement calcul des prédicats est une formalisation du langage des mathématiques proposée par les logiciens du début du XXe siècle.
Le trait caractéristique de la logique du premier ordre est l'introduction d'un ensemble de symboles désignant des variables, d'un ensemble de symboles désignant des fonctions, d'un ensemble de symboles désignant des prédicats, ainsi que des connecteurs logiques et deux symboles

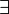
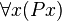
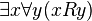
Les formules logiques déduites de ce calcul des prédicats ont pour but de s'appliquer à n'importe quel modèle, c’est-à-dire n'importe quel ensemble dans lequel les variables, les fonctions, les prédicats du calcul représentent respectivement des éléments de l'ensemble, des fonctions de cet ensemble dans lui-même, et des parties de cet ensemble. Les prédicats représentent des qualités, s’ils sont à une place (unaires), ou des relations n-aires, entre n individus de cet ensemble. Ces notions seront précisées dans la suite de cet article.
Le calcul des propositions est une version réduite du calcul des prédicats, sans les quantificateurs

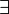
On parle de logique du premier ordre par opposition aux logiques d'ordre supérieur, où l'on peut quantifier aussi bien les variables que les prédicats ou les fonctions.
Formation d'une formule du calcul des prédicats du premier ordre
Syntaxe
Cette section donne une brève présentation de la grammaire du calcul des prédicats dans un langage formel couramment utilisé en logique classique par la plupart des mathématiciens. Mais le calcul des prédicats n’est pas limité aux théories purement mathématiques. L’article Prédicat donne une présentation moins formelle, dans un langage semi-naturel, qui montre plus clairement pourquoi la grammaire des prédicats est universelle.
On se donne un langage L défini par :
- V un ensemble de symboles appelés variables, toujours infini.
- C un ensemble de symboles appelés constantes, éventuellement vide.
- P un ensemble de symboles de prédicats
- F un ensemble de symboles de fonctions, éventuellement vide.
Chaque symbole de prédicat ou de fonction a une arité (un entier strictement positif) qui détermine le nombre d'arguments ou d'objets auxquels il est appliqué.
- les symboles

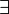
- les symboles

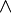
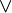

- les symboles de ponctuation ")" et "(".
On pourrait se contenter d'un seul quantificateur


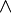
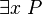
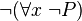
On appellera termes les formules composées ainsi :
- x, élément de V , est un terme,
- x, élément de C , est un terme,
- si f est un symbole de fonction n-aire et
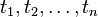
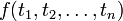
Un terme est clos s'il ne contient pas de nom de variable.
Les termes ont pour but de représenter les objets sur lesquels vont s'appliquer des prédicats. Appelons T l'ensemble des termes.
Les énoncés ou formules du calcul des prédicats du premier ordre sont les suivants, et uniquement les suivants (appelons E l'ensemble des énoncés) :
-
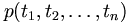
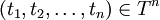
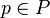
-
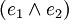
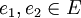
-
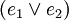
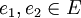
-
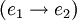
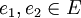
-
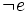
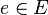
-
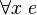
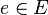
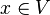
-
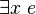
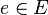
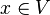
Les énoncés ont pour but de représenter des propositions susceptibles d'être vraies ou fausses.
Exemples
- Exemple 1
Si on se donne pour constantes les deux symboles 0 et 1, pour symboles de fonctions binaires + et ., et pour symboles de prédicats binaires les symboles = et <, alors le langage utilisé peut être interprété comme étant celui de l'arithmétique. x et y désignant des variables, x+1 est un terme, 0+1+1 est un terme clos, x<y+1 est une formule, 0+1+1<0+1+1+1 est une formule close.
- Exemple 2
Si on se donne un ensemble de variables quelconque, une constante notée e, un symbole de fonction binaire noté *, un symbole de fonction unaire notée -1, un symbole de relation binaire =, alors le langage utilisé peut être interprété comme étant celui de la théorie des groupes. Si x et y désignent des variables, x*y est un terme, e*e est un terme clos, x=y*y est une formule, e=e*e-1 est une formule close.
Prédicats, formules closes, variables libres, variables liées
Lorsqu’une variable x appartient à une sous-formule précédée d’un quantificateur,
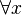
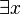
La distinction entre variable libre et variable liée est importante. Une variable liée ne possède pas d'identité propre et peut être remplacée par n'importe quel autre nom de variable qui n'apparaît pas dans la formule. Ainsi,
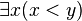
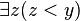
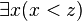
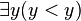
Une formule close est une formule dont toutes les variables sont liées. Un prédicat est une formule qui contient une ou plusieurs variables libres. On peut considérer les prédicats comme des concepts (voir Prédicat). Ainsi,
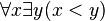
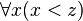
But du calcul des prédicats
Comme le calcul des propositions, le calcul des prédicats se donne pour but de définir quels sont les énoncés qui sont valides et quels sont ceux qui ne le sont pas. Et comme pour le calcul des propositions, il existe deux façons d'aborder cette question, l'aspect sémantique et l'aspect syntaxique. Un théorème de complétude montre l'équivalence entre ces deux aspects.
Sémantique du calcul des prédicats du premier ordre
La théorie de la vérité des formules du calcul des prédicats a été appelée par Tarski sa sémantique. Elle est présentée dans l'article Théorie des modèles. Un modèle d'un langage du premier ordre est un ensemble dans lequel on donne un sens aux symboles du langage. On peut alors attribuer une valeur de vérité (vrai ou faux) aux formules du langage dans ce modèle. On dit qu'une formule F du langage est un théorème si cette formule est vraie dans tout modèle du langage, ce qu'on note
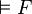
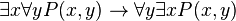
-
- Ou bien il existe un élément a de M tel que
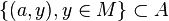
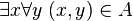
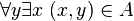
- Ou bien un tel a n'existe pas et la proposition
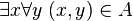
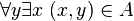
- Ou bien il existe un élément a de M tel que
L'implication étant vraie dans tout modèle, la formule est valide.
Par contre, la formule
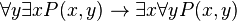
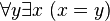
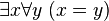
Syntaxe du calcul des prédicats
Dans le calcul des prédicats, on peut également déduire des formules au moyen de déductions relevant d'un calcul. Une déduction consiste à partir d’hypothèses, ou d’axiomes, et à progresser par étapes logiques jusqu’à une conclusion selon des règles prédéfinies. Il existe plusieurs présentation possible de ces axiomes et de ces règles.
- La déduction naturelle. Les principes logiques y sont présentés d’une façon aussi proche que possible des raisonnements naturels. Elle consiste en une liste de treize règles. Elles pourraient être réduites à un plus petit nombre, mais l'évidence des principes serait moins naturelle.
- Les axiomes logiques. Plusieurs systèmes d’axiomes équivalents peuvent être proposés. Cette approche adoptée par presque tous les logiciens depuis les Principia Mathematica de Whitehead et Russell a une grande importance à la fois métamathématique et historique. L'un des systèmes d'axiomes le plus court consiste en :
-
- les axiomes du calcul des propositions
-
- les axiomes relatifs au quantificateur

-
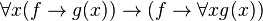
-
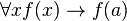
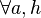
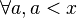
-
- La règle du modus ponens : si on a prouvé
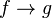
- La règle de généralisation : si on a prouvé f(x), alors on a prouvé
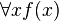
- les axiomes du calcul des propositions
Mais si la recherche de systèmes d'axiomes minimaux met en évidence les principes élémentaires sur lesquels peuvent s'appuyer tous les raisonnements, elle ne montre pas le caractère d’évidence naturelle des principes logiques plus généraux.
- La logique du dialogue apporte également un autre éclairage sur la nature des lois logiques.
- Voir aussi correspondance de Curry-Howard.
Quelle que soit la présentation abordée, les axiomes et règles peuvent être codés de façon à ce qu'une machine puisse vérifier la validité ou non d'une déduction conduisant à une formule F. Si la déduction est correcte, la formule F est dite prouvable, ce qu'on note
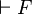
Se pose alors la question suivante : y a-t-il équivalence entre la présentation sémantique et la présentation syntaxique ?
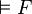
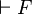
- Toute formule prouvable est-elle un théorème ? Si la validité de F est attestée par un calcul syntaxique, F est-elle valide dans tout modèle du langage utilisé ?
- Réciproquement, si F est un théorème, valide dans tout modèle, peut-on montrer sa validité à la suite d'un calcul syntaxique ?
C'est à cette question que répond le théorème de complétude qui suit.
Complétude et indécidabilité
Emmanuel Kant croyait à tort que la logique de son temps, celle d’Aristote, était une science complète et définitivement achevée (préface de la seconde édition de la critique de la raison pure, 1787). Les logiciens du dix-neuvième siècle se sont rendus compte que la théorie d’Aristote ne dit rien ou presque sur la logique des relations. Gottlob Frege et beaucoup d'autres ont comblé cette lacune en définissant le calcul des prédicats au premier ordre.
Kurt Gödel a prouvé en 1929 (dans sa thèse de doctorat) que le calcul des prédicats est complet, au sens où on peut donner un nombre fini de principes (axiomes logiques, schémas d'axiomes logiques et règles de déduction) qui suffisent pour déduire de façon mécanique toutes les lois logiques (voir le théorème de complétude de Gödel). Il y a équivalence entre la présentation sémantique et la présentation syntaxique du calcul des prédicats. Toute tautologie (propriété vraie dans tout modèle du langage utilisé) est un théorème c'est-à-dire qu'elle peut être déduite d'un calcul, soit au moyen de la déduction naturelle, soit au moyen des axiomes logiques, et réciproquement. La logique du premier ordre est donc achevée au sens où le problème de la correction logique des démonstrations y est résolu. Elle continue cependant à faire l’objet d’importantes recherches : théorie des modèles, algèbres cylindriques, mécanisation du raisonnement... On notera qu'il existe d'autres théories qui ne sont pas complètes. Ainsi, Gödel a prouvé en 1930 que les théories des ensembles et, plus généralement, toutes les théories mathématiques qui contiennent certaines vérités arithmétiques élémentaires, ne sont pas complètes, au sens où elles ne permettent pas de prouver toutes les vérités qu'elles permettent pourtant d'énoncer (voir théorème d'incomplétude de Gödel).
Le calcul des prédicats est semi-décidable, dans le sens où une machine peut dresser, les uns après les autres, la liste des théorèmes de cette logique. Mais, contrairement au calcul des propositions, il n'est pas décidable dans le sens où, si on se donne une formule F, il n'est pas possible de décider si F est un théorème ou non, si on ne dispose pas de sa preuve. En effet, la confrontation de F avec la liste des théorèmes se terminera si F est effectivement un théorème, mais dans l'attente de la terminaison, on ne sait pas si le calcul des théorèmes n'a pas été mené assez loin pour identifier F comme théorème ou si ce calcul ne se terminera pas parce que F n'est pas un théorème. Par contre le calcul des prédicats monadiques (n'ayant que des symboles de propositions unaires et pas de symbole de fonction) est décidable.