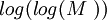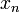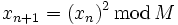Blum Blum Shub - Définition

Blum Blum Shub (BBS) est un algorithme capable de générer des nombres pseudo-aléatoires. Il fut proposé en 1986 par Lenore Blum, Manuel Blum et Michael Shub, d'où son nom.

On calcule la sortie de BBS en itérant la suite :

Avec , le produit de deux grands nombres premiers et , et la sortie de l'algorithme est le bit le moins significatif (least signifiant bit ou LSB) de . Alternativement, la sortie peut être plusieurs des derniers bits de

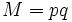
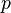
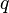
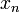
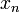
Les deux nombres premiers, et , devraient tous deux être congruents à 3 modulo 4 (cela garantit que chaque résidu quadratique possède une racine carrée qui possède également un résidu quadratique) et doit être petit (ce qui fait que le cycle est long).

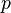
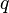
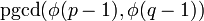
Sécurité de l'algorithme

Le générateur n'est pas approprié aux simulations, mais plutôt à la cryptographie, car il est assez lent.

Cependant, il possède une sécurité inhabituelle, puisqu'il à été démontré qu'il était cryptographiquement sûr sous l'hypothèse qu'il soit difficile de factoriser un produit de grand nombres premiers, et que au plus bits de poids faible de chaque soient sortis à chaque itération. Dans ce cas, il n'est pas possible de différencier la suite produite d'une suite réellement aléatoire.