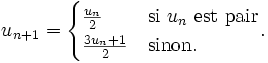Conjecture de Syracuse - Définition

La conjecture de Syracuse ressemble à un jeu de calcul. On prend n’importe quel nombre entier plus grand que 1 (2, 3, 73, 153…); s’il est pair, on le divise par 2; s’il est impair, on le multiplie par 3 et on ajoute 1. En réitérant l’opération plusieurs fois, on obtient une suite de nombres… qui finit toujours par aboutir à 1.

Cette suite de Syracuse se défnit de la manière suivante :

La conjecture affirme que, quel que soit le terme initial N de la suite, celle-ci finit inexorablement par boucler sur 4, 2, 1. Par exemple, en commençant par N = 6, nous obtenons la suite : 6, 3, 10, 5, 16, 8, 4, 2, 1. Sous son apparente simplicité, elle défie encore les mathématiciens actuels.

Elle est appelée conjecture de Syracuse, conjecture de Collatz, conjecture du 3n+1 ou conjecture d'Ulam. Les nombres qui la composent sont désignés comme suite de Syracuse ou comme suite de grêlons (car les nombres " montent " de façon chaotique et " chutent " souvent de façon brusque).

Origines

Les noms multiples de cette suite prouvent la difficulté d'en retrouver la paternité exacte. La naissance de ce problème semble se situer autour des années 1950. Helmut Hasse, un ami de Lothar Collatz, de visite à l'université américaine de Syracuse propose le problème aux universitaires. Celui-ci remporte un vif succès et la suite de Collatz, appelée aussi algorithme de Hasse prend alors le nom de suite de Syracuse. Entre-temps, le mathématicien polonais Stanislas Ulam le répand dans le Laboratoire national de Los Alamos et la suite devient la suite d'Ulam. Dans les années 1960, le problème est repris par le mathématicien S. Kakutani qui le diffuse dans les universités de Yale et Chicago. Le problème prend alors le nom de problème de Kakutani.

L'étude de cette suite a donné lieu à la création d'un vocabulaire très imagé comme le temps de vol, le temps de vol en altitude, l'altitude maximale, le facteur d'expansion.

Cette conjecture mobilisa tant les mathématiciens durant les années 60, en pleine guerre froide, qu'une blague courut selon laquelle ce problème serait l'œuvre d'un complot soviétique pour ralentir la recherche américaine. Plus sérieusement, Paul Erd?s dit à propos de la conjecture de Collatz : " les mathématiques ne sont pas encore prêtes pour de tels problèmes ". Il proposa une offre de 500 $ à quiconque lui donnerait une solution.

Première approche et vocabulaire

suite de Syracuse pour N = 15

suite de Syracuse pour N = 127

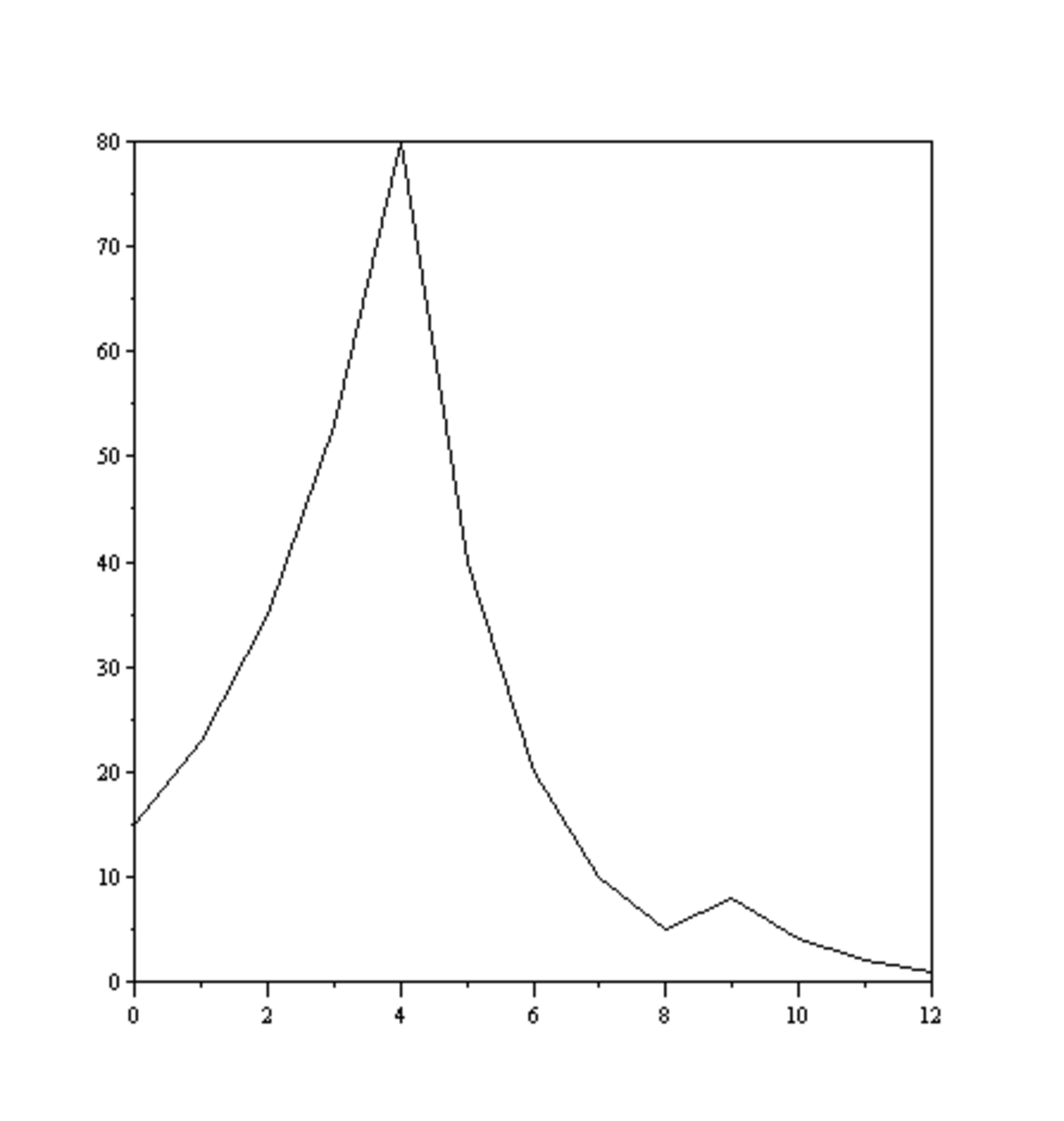
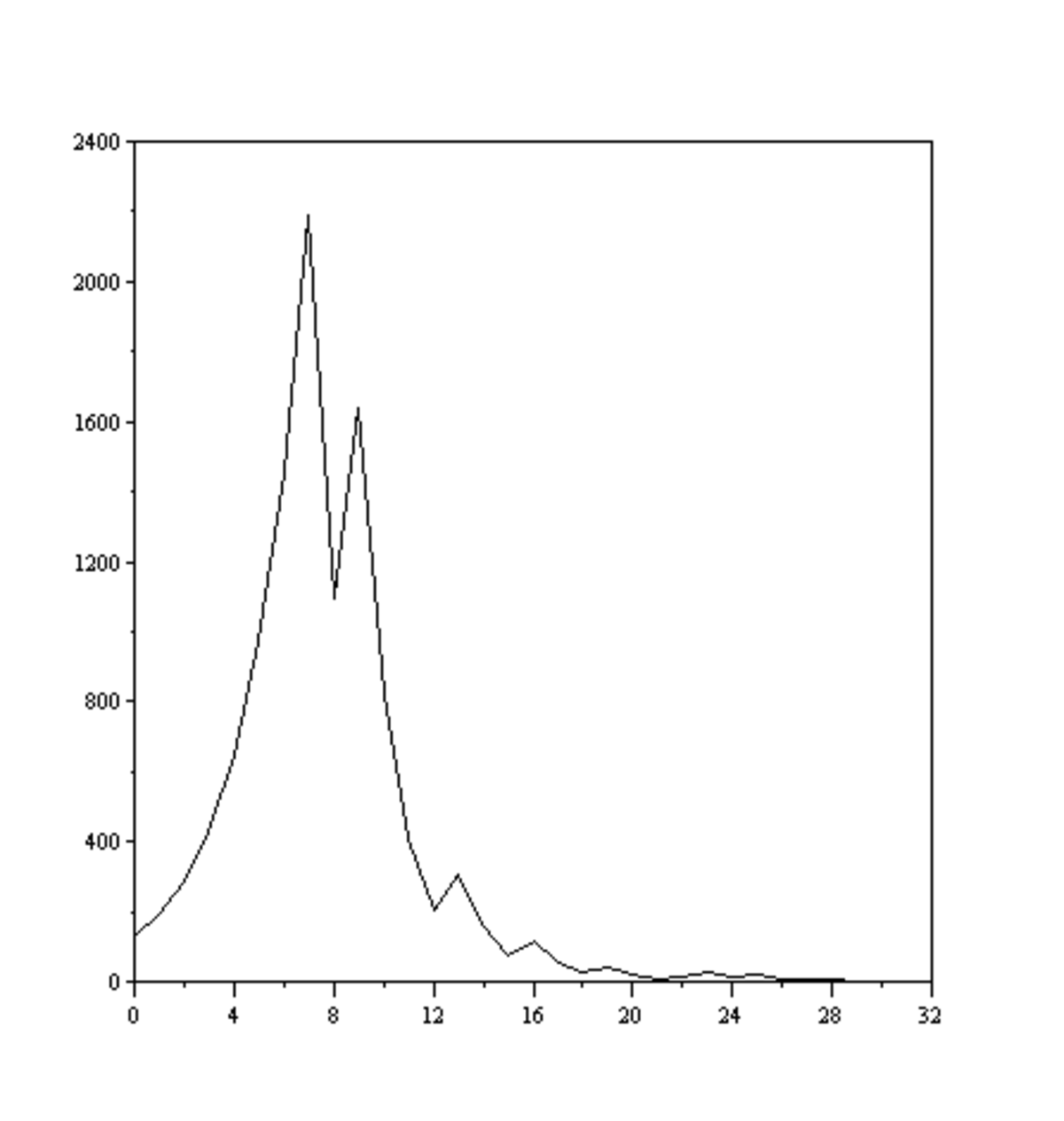
Le calcul de la suite pour N = 7 : (7 , 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1) laisse déjà entr'apercevoir que la suite peut prendre des valeurs assez grandes avant de retomber à 1. L'observation graphique de la suite pour N = 15 et N = 127 montre que la suite peut monter assez haut avant de redescendre. C'est de cette observation qu'est né le vocabulaire sur l'étude de cette suite. En observant ces graphiques, on a l'impression d'y voir la trajectoire d'une feuille emportée par le vent.

On parle donc du vol de la suite. On définit alors

• le temps de vol: c'est le plus petit indice n tel que u_n = 1

Il est de 17 pour la suite de Syracuse 15 et de 46 pour la suite de Syracuse 127

• le temps de vol en altitude  : c'est le plus petit indice n tel que u_n+1< N

Il est de 10 pour la suite de Syracuse 15 et de 23 pour la suite de Syracuse 127

• l'altitude maximale : c'est la valeur maximale de la suite

Elle est de 160 pour la suite de Syracuse 15 et de 4372 pour la suite de Syracuse 127

• Le facteur d'expansion: c'est le rapport entre le nombre de départ et l'altitude maximale

Exemple détaillé : Voici la suite du vol N = 15 : (15, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1).

U₀ = 15, U₁ = 46, ..., U₁₇ = 1.Le temps de vol est donc de 17.

n = 10 est le plus petit n tel que U₁₁<15 (car U₁₁ = 10, et 15>10).

La valeur de n la plus grande de la liste est 160, c'est donc la valeur de l'altitude maximale...

Enoncés équivalents

On rencontre parfois une relation de récurrence de la forme

Qui ne change pas fondamentalement le problème mais qui réduit le temps de vol.

Des énoncés équivalents de la conjecture existent

• si on arrête la suite dès qu'elle atteint 1, la conjecture peut s'exprimer par pour tout N, la suite possède un nombre fini de termes impairs (resp pairs)
• Pour tout N, la suite possède une durée de vol finie
• Pour tout N, la suite possède une durée de vol en altitude finie

Quelques résultats

Il est facile de démontrer que si la suite commençant par k2^p - 1 a une durée de vol finie, il en est de même de la suite commençant par k3^p - 1 .

Si on suppose comme hypothèse de récurrence que tout entier non nul N' < N a une durée de vol finie et si N est de la forme 4k+1 ou 4k ou 4k+2, alors N a également une durée de vol finie. Une tentative est donc faite de travailler sur la forme de N pour diminuer le nombre de cas à étudier.

Une autre voie d'exploration est une étude systématique par ordinateur de tous les cas. Jusqu'à présent, les ordinateurs ont prouvé la conjecture pour tout N < 2⁶² (juin 2004- Eric Roosendaal ou T. Oliveira e Silva)

Des corrélations ont été cherchées entre le nombre N de départ et la durée de vol, ou le record d'altitude. On a ainsi observé que si les records d'altitude pouvaient être très élevés, la durée du vol était en comparaison plus modeste. Une observation sur les nombres déjà étudiés semble indiquer que l'altitude maximale est voisine de φ(N).N² où φ(N) serait une fonction quasi-constante. Le temps de vol est plus erratique mais semble en général ne pas dépasser une fonction proportionnelle à ln(N)

Il existe des arguments heuristiques et statistiques qui renforcent la conjecture : si nous considérons uniquement les nombres impairs de la suite générée par le processus de Collatz, alors nous pouvons arguer qu'en moyenne le prochain nombre impair vaudra environ 3/4 du précédent, ce qui suggère qu'ils diminueront pour atteindre 1.

D'autres chercheurs comme J. Conway penchent pour l'indécidabilité de la conjecture. Ils tentent de travailler en élargissant le champ d'étude à d'autres suites du même type (problème 5n +1 etc).

La fonction de Syracuse

Soit k un entier naturel impair, écrivons 3k+1 sous la forme 2ⁿk' , n ≥ 1, k’ impair et posons f(k) = k′. Nous définissons ainsi une application de l'ensemble I des nombres impairs vers lui-même appelée fonction de Syracuse. La composée sera notée f ⁿ.

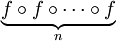
Propriétés de la fonction de Syracuse : on peut démontrer que

• f(4k + 1) = f(k)
• Pour tout h pair, f(2h - 1) = 3h - 1
• Pour tout h impair, f(2h - 1) ≤ (3h - 1)/2
• pour tout p ≥ 2 et h impair,

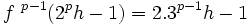
Démontrer la conjecture de Syracuse, c'est prouver que pour tout k ∈ I , il existe un entier n ≥ 1 tel que : f ⁿ(k) = 1.

Désignons par E l'ensemble des nombres impairs k ∈ I pour lesquels il existe un entier n ≥ 1 tel que : f ⁿ(k) = 1. Il s'agit de montrer que E = I.

Une preuve possible par récurrence peut être amorcée de la manière suivante :

On sait par exemple que 1, 3, 5, 7, 9 sont dans E.

Soit k un nombre impair ≥11. Supposons que 1, 3, 5,..., k - 2 sont dans E et essayons de montrer que k est dans E. Comme k est impair, k + 1 est pair, il s'écrit sous la forme 2^ph, p ≥ 1, h impair, et k = 2^ph-1

• Si p = 1, k = 2h - 1. Il est facile de vérifier que f(k) < k , donc f(k) ∈ E, et par suite k ∈ E.
• Si p ≥ 2 et h multiple de 3 on peut écrire h = 3h′. Soit k′ = 2^p+1h′ - 1; nous avons f(k′) = k et comme k′< k , k′ est dans E donc k = f(k′) ∈ E
• Si p ≥ 2 et h non multiple de 3 mais h est congru à (-1)^p mod 4, nous pouvons montrer encore que k ∈ E. (Cf.)

Le cas problématique est celui où p ≥ 2, h non multiple de 3 et h congru à (-1)^p+1 mod 4. Dans ce cas, si on arrive à démontrer que pour tout nombre impair k' compris largement entre 1 et k-2 on a 3k' ∈ E on peut conclure.(Cf.).