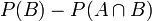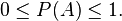Axiomes des probabilités - Définition

Commençons par donner une définition simple d'une probabilité. Considérons une expérience aléatoire (ou épreuve aléatoire), et l'univers associée à cette expérience (ensemble de tous les résultats possibles).

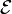
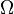
Une probabilité est une application qui, à un évènement quelconque lié à l'expérience aléatoire , associe un nombre réel (noté ), de telle manière que satisfasse les axiomes de Kolmogorov :

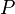
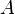
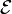
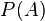
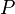
Premier axiome

Pour tout évènement  :

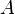
C'est-à-dire que la probabilité d'un évènement est représentée par un nombre réel compris entre 0 et 1.

Deuxième axiome

.

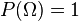
C'est-à-dire que la probabilité de l'évènement certain, ou d'obtenir un quelconque résultat de l'univers, est égale à 1. Autrement dit, la probabilité de réaliser l'un ou l'autre des évènements élémentaires est égale à 1.

Troisième axiome

Toute suite d'évènements deux à deux disjoints (on dit aussi : deux à deux incompatibles), satisfait:

.

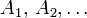
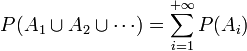
C'est-à-dire que la probabilité d'un évènement qui est la réunion (dénombrable) disjointe d'évènements est égale à la somme des probabilités de ces évènements. Ceci s'appelle la σ-additivité, ou additivité dénombrable (si les évènements ne sont pas deux à deux disjoints, cette relation n'est plus vraie en général).

Ces trois axiomes sont connus comme étant les axiomes de Kolmogorov, du nom d'Andrei Nikolaievitch Kolmogorov, mathématicien russe qui les a développés.

D'une manière plus théorique, une probabilité peut être définie comme une mesure sur une σ-algèbre ou tribu de sous-ensembles d'un univers (ces sous-ensembles étant les évènements), telle que la mesure de l'univers soit égale à 1.

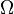
Cette propriété est importante, puisqu'elle nous amène naturellement au concept de probabilité conditionnelle. Tout évènement de probabilité non nulle définit une autre probabilité sur l'univers :

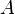
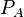
pour tout évènement de , on pose :

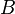
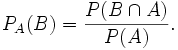
Le réel se note aussi et habituellement se lit " la probabilité conditionnelle de , sachant  " ou " la probabilité de , sachant que s'est réalisé ".

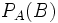
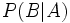
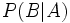
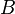
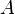
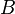
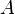
Propriétés d'une probabilité

À partir des axiomes, se démontrent un certain nombre de propriétés utiles pour le calcul des probabilités, par exemple :

• .

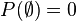
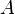
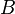
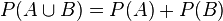
• si , sont deux évènements incompatibles, alors .

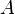
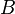
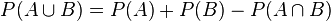
• pour tous évènements , , .

Ceci signifie que la probabilité pour que l'un au moins des évènements ou se réalise est égale à la somme des probabilités pour que se réalise, et pour que se réalise, moins la probabilité pour que et se réalisent simultanément.

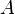
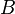
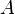
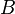
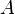
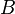
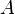
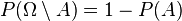
• pour tout évènement , .

Ceci signifie que la probabilité pour qu'un évènement ne se produise pas est égale à 1 moins la probabilité pour qu'il se réalise ;

cette propriété s'utilise lorsqu'il est plus simple de déterminer la probabilité de l'évènement contraire que celle de l'évènement.

• ; en particulier, si , alors

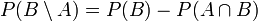
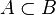
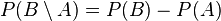
(il en résulte que si , alors  : c'est la propriété de croissance de la probabilité).

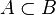
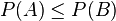
La relation précédente signifie que la probabilité que B se réalise, mais pas A, est égale à la différence .