Axiome du choix - Définition
L'axiome du choix, abrégé en " AC ", est un axiome de la théorie axiomatique des ensembles.
Énoncé
Dans sa forme première, l'axiome du choix s'énonce littéralement comme suit :
- " Étant donnée une famille non vide d'ensembles non vides, il existe une fonction, appelée fonction de choix qui à chacun d'entre eux associe un de ses éléments. "
Cet axiome se traduit par le prédicat :
![(\forall X)\; \left[X\neq \emptyset\wedge (\emptyset \notin X)\right]\Longrightarrow\left[ \exists f:X\rightarrow \bigcup_{Y\in X} Y,\; \forall x\in X, \; f(x)\in x \right]\;](https://static.techno-science.net/illustration/Definitions/autres/a/ae90fac0907f572729078f5c56c7ea33_a5701411318181ba793ab8e6cecdc0bb.png)
Autres formulations
Il existe d'autres énoncés équivalents à l'axiome du choix, dont les suivants :
- " Le produit d'une famille non vide d'ensembles non vides est non vide " :
![(\forall X)\; \left[X\neq \emptyset \wedge (\emptyset \notin X)\right]\Longrightarrow \prod_{y\in X}y\neq \emptyset\;](https://static.techno-science.net/illustration/Definitions/autres/d/dafb59eb374b6b285b02bd897f64e8fc_57184979ec981792f3f462d06dee17c9.png)
- " Toute surjection sur un ensemble non vide est inversible à droite " ;
- Pour toute relation d'équivalence R sur un ensemble non vide X, il existe un choix de représentants de R, autrement dit un sous-ensemble Y de X tel que tout élément de X est R-équivalent à un unique élément de Y.
- Théorème de Zermelo : " Tout ensemble non vide est bien ordonnable (c'est-à-dire peut être muni d'une structure de bon ordre) " ;
- Lemme de Zorn : " Tout ensemble inductif non vide admet un élément maximal " ;
- L'axiome du choix est équivalent au premier énoncé.
Si X est une famille non vide d'ensembles non vides, le produit
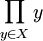
- L'axiome du choix est équivalent au second énoncé.
Pour X une famille non vide d'ensembles non vides, on note Y la réunion disjointe des ensembles appartenant à X. Il existe une surjection naturelle
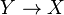
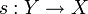
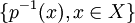
- L'axiome du choix est équivalent au troisième énoncé.
Si X est une famille non vide d'ensembles non vides, si Y est la réunion disjointe des ensembles de X, il existe une relation d'équivalence naturelle sur Y : deux éléments sont dits équivalents s'ils appartiennent à un même ensemble de X. Réciproquement, si R est une relation d'équivalence sur un ensemble non vide Y, l'ensemble X des classes d'équivalence est une famille non vide d'ensembles non vides. Une fonction de choix de X est exactement un choix d'un ensemble de représentants de R.
- Le lemme de Zorn implique l'axiome du choix.
Soit X une famille non vide d'ensembles non vides. Soit I l'ensemble des fonctions de choix f pour une sous-famille Y de X. L'ensemble I est non vide, car il est possible de définir sans l'axiome du choix une fonction de choix sur toute sous-famille finie de X. Cet ensemble est ordonné par le prolongement des applications. I est un ensemble inductif. Si le lemme de Zorn est vérifié, I admet un élément maximal, autrement dit une fonction de choix définie sur une sous-famille maximale Y de X. Si par l'absurde Y était différent de X, associer à un ensemble appartenant à X-Y un de ses éléments est toujours possible et permettrait de prolonger f à une sous-famille strictement plus grande, ce qui contredit la maximalité. Donc, Y=X et f est une fonction de choix pour X.
- Le théorème de Zermelo implique l'axiome du choix.
Soit X une famille non vide d'ensembles non vides. Soit Y la réunion des ensembles appartenant à X. Par le théorème de Zermelo, Y peut être muni d'un bon ordre <. Tout ensemble de X est une partie de Y et on peut donc lui associer son minimum, élément de X. On définit ainsi une fonction de choix pour X.
Particularités
Cet axiome fait partie des axiomes optionnels et controversés de la théorie des ensembles. En effet, l'existence d'un objet défini à partir de l'axiome du choix n'est pas une existence constructive, c’est-à-dire que l'axiome ne décrit aucunement comment construire l'objet dont on affirme l'existence. Ainsi, dire qu'il existe une base de l'espace vectoriel des fonctions continues ne permet en aucune façon de dire comment décrire une telle base. De ce point de vue, l'axiome du choix peut paraître d'un intérêt limité et c'est pourquoi certains mathématiciens se montrent plus satisfaits d'une démonstration s'ils peuvent éviter d'avoir recours à cet axiome du choix. Mais la plupart des mathématiciens l'utilisent sans réticence particulière.
L'axiome du choix ne fait pas partie du jeu d'axiomes de la théorie des ensembles ZF. On appelle théorie ZFC, la théorie ZF munie en plus de l'axiome du choix.
Anecdote
Bertrand Russell disait à propos de l'axiome du choix : Pour choisir une chaussette plutôt que l'autre pour chaque paire d'une collection infinie, on a besoin de l'axiome du choix. Mais pour les chaussures, ce n'est pas la peine.
Explication :
- Quand on dispose d'une paire de chaussettes quelconque, on n'a aucun moyen a priori de distinguer une chaussette de l'autre, ce sont des objets a priori identiques et même si chaque matin on arrive à choisir laquelle on va mettre en premier, on serait bien en peine de trouver un procédé général (algorithme) qui nous permette de renouveler l'exploit éternellement.
- Pour les chaussures, il existe un moyen de choisir qui marche tout le temps (une fonction de choix naturelle) : choisir toujours la chaussure gauche (ou droite) puisqu'il y a toujours une chaussure gauche et une chaussure droite. On dispose ainsi d'un algorithme simple.
Il semble cependant qu'il faille tempérer le pessimisme de Russell[1].
Exemples où l'axiome du choix est nécessaire
- L'ensemble externe * R des hyperréels doit son existence à l'axiome de choix.
- Un ensemble fini au sens de Dedekind est un ensemble fini.
Formes faibles de l'axiome du choix
Il existe des formes faibles de l'axiome du choix que le mathématicien utilise couramment, la plupart du temps sans s'en apercevoir à moins d'être logicien ou " constructiviste ", et qui servent à " construire " des suites. Ils sont absolument indispensables pour l'exposé usuel des fondements de l'analyse.
Axiome du choix dénombrable
Cet axiome, abrégé en " AD ", est la restriction de l'axiome du choix aux familles dénombrables :
-
- " Etant donnée une famille dénombrable d'ensembles non vides, il existe une fonction qui à chacun d'entre eux associe un de ses éléments. "
Il est par exemple utilisé pour démontrer qu'une fonction f définie sur R est continue en 0 ssi f(xn) tend vers f(0) pour toute suite (xn) tendant vers 0. Il permet aussi de démontrer qu'un produit dénombrable d'espaces compacts est compact, ou encore le théorème de Hahn-Banach pour un espace de Banach séparable. Il permet également de démontrer le théorème des complets emboîtés (dont l'une des conséquences est le théorème de Baire).
Attention à une confusion courante: c'est la famille d'ensembles qui est dénombrable, aucune hypothèse n'étant faite sur les ensembles composant cette famille. L'axiome du choix dénombrable ne concerne pas la question du choix d'un élément dans un ensemble dénombrable mais la possibilité de faire une infinité dénombrable de choix simultanément.
Axiome du choix dépendant
Cet axiome, abrégé en " DC ", assure que, si R est une relation sur un ensemble non vide E vérifiant
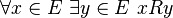
il existe une suite (xn) d'éléments de E telle que
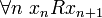
L'axiome DC implique l'axiome AD, sans que cela soit évident. Il est par exemple utilisé dans axiome de fondation et plus généralement relation bien fondée pour établir l'équivalence de deux définitions.