Théorème des valeurs intermédiaires - Définition

Le théorème des valeurs intermédiaires est un théorème important en analyse et concerne des fonctions continues sur un intervalle.

Énoncé

Théorème des valeurs intermédiaires

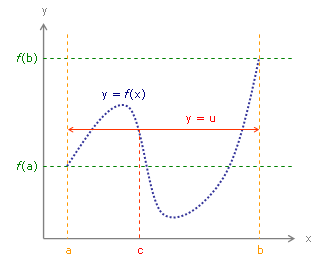
Soit f une fonction de dans , continue sur un intervalle I.

Alors pour tous réels a et b de I, pour tout réel k compris entre f(a) et f(b), il existe au moins un réel c compris entre a et b tel que f(c) = k.

Cas particulier : si f(a) ≤ 0 et f(b) ≥ 0, il existe au moins un réel c compris entre a et b tel que f(c) = 0 (car 0 est compris entre f(a) et f(b)).

Remarques

• La propriété de la valeur intermédiaire correspond à une notion intuitive: il est possible de dessiner le graphe de la fonction d'un seul trait de crayon. Ou dit autrement, il n'est pas nécessaire de soulever son crayon pour dessiner le graphe de la fonction.

• Cette remarque amène à se poser la question : n'y a-t-il pas équivalence entre la propriété de la valeur intermédiaire et la continuité? La réponse est malheureusement négative. Un contre exemple nous est donné par la fonction réelle de la variable réelle définie par si et . Cette fonction n'est pas continue en 0 mais elle satisfait bien la propriété de la valeur intermédiaire pour chaque couple de points dans .

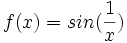
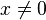
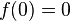
• Ce théorème est essentiel à l'élaboration de la théorie de l'analyse élémentaire, il permet la démonstration du théorème de la bijection et la construction de nombreuses fonctions élémentaires comme la racine carrée.

• Ce théorème est faux sur le corps des nombres rationnels. Il faut nécessairement utiliser les propriété du corps des nombres réels. Par exemple, la fonction f (x) = x² - 2 de Q dans Q est continue sur [ 0 ; 2], et vérifie f (0) = - 2, f (2) = 2. Cependant, il n'y a pas de nombre rationnel x tel que f (x) = 0.

• Ce théorème met en valeur une propriété topologique des nombres réels. Il se démontre simplement à l'aide de la topologie ou de manière plus délicate si l'on procède manuellement.

• Lorsque l'on cherche à démontrer qu'il existe une solution unique, on regarde si de plus f est strictement monotone. Il est aussi possible d'utiliser le théorème de la bijection.

Applications

• On utilise souvent ce théorème pour montrer que deux fonctions continues sur un même intervalle et dont la différence change de signe aux bornes de cet intervalle prennent la même valeur en au moins un point de cet intervalle.

Exemple : Soient f et g deux fonctions continues sur un intervalle non vide [a ;b] de , telles que g(a) - f(a) et g(b) - f(b) soient de signes contraires. Il existe au moins un réel c compris entre a et b et tel que f(c) = g(c).

En effet, posons φ = f - g. La fonction φ est continue, et 0 est compris entre φ(a) et φ(b). Il existe donc au moins un réel c compris entre a et b et tel que φ(c) = 0, soit encore f(c) = g(c).

Dans le cas particulier où g est l'identité sur l'intervalle [a;b] et où f(a) > a et f(b) < b, on obtient un théorème de point fixe (Brouwer en dimension 1).

• Pour tout polynôme P à coefficients réels et de degré impair, il existe au moins une racine réelle, c'est-à-dire un réel c tel que P(c) = 0.

En effet, on peut supposer (sans perte de généralité) que le coefficient du terme de plus haut degré de P est égal à 1. Alors, comme le degré de P est impair, P(x) tend vers -∞ quand x tend vers -∞, et P(x) tend vers +∞ quand x tend vers +∞. On en déduit qu'il existe a réel tel que P(a) ≤ 0, et qu'il existe b réel tel que P(b) ≥ 0. Comme P est continu, il existe au moins un réel c compris entre a et b et tel que P(c) = 0.

Note historique

Il n'est pas nécessaire qu'une fonction soit continue pour que la conclusion du théorème des valeurs intermédiaires soit vraie. En 1875, Gaston Darboux a montré que cette conclusion était vérifiée par les fonctions dérivées, qu'elles soient continues ou non (voir Théorème de Darboux (analyse) ).

Résolution et démonstration

Le théorème des valeurs intermédiaires fait partie des théorèmes dits d'existence. A la question " Existe-t-il un réel c tel que f(c) = k?  ", le théorème répond " OUI, il en existe ". Il fait naître alors nécessairement la question suivante " Quel est ce réel c ? "

En général, un théorème d'existence ne donne aucun moyen de trouver l'un des éléments dont il affirme l'existence. C'est le cas de la première démonstration, plus courte et plus simple mais qui s'appuie sur une théorie plus difficile, la topologie. Ce n'est pas le cas pour la deuxième démonstration qui fournit un algorithme de résolution appelé méthode de dichotomie.

Démonstration avec la topologie

Les connexes de sont les intervalles. L'ensemble de départ est donc un connexe. L'image d'un connexe par une fonction continue est un connexe. Donc l'image par f de est un intervalle, ce qui démontre le théorème.

Démonstration sans théorème topologique

Le principe consiste à couper l'intervalle de départ en deux et à conserver l'intervalle où l'on sait que se trouve une solution. On recommence ensuite en coupant en deux l'intervalle conservé, etc. On obtient ainsi des intervalles emboîtés de plus en plus petits dans lesquels on est sûr de trouver une solution. On finit alors par trouver un encadrement " assez fin " de la solution.

On suppose donc que

• la fonction f est continue sur l'intervalle [a , b]
• f(a) < k < f(b) (une démonstration analogue peut se faire pour f(a) > k > f(b)).

La continuité de la fonction f va permettre d'utiliser la propriété suivante :

si (u_n) est une suite à valeurs dans [a ; b] convergeant vers L, alors f(u_n) converge vers f(L).

La méthode de dichotomie consiste à construire une suite d'intervalles I_n = [a_n ; b_n] tels que pour tout n :

• I_n+1 soit inclus dans I_n
• la longueur de I_n+1 soit la moitié de celle de I_n
• f(a_n) < k < f(b_n).

On procède de la manière suivante :

• on pose initialement I₀ = [a ;b]
• quand à un rang n, l'intervalle I_n est construit, on note m_n son milieu et
  • si f(m_n) < k , on prend pour I_n+1 l'intervalle [m_n ; b_n] et on pose a_{n + 1} = m_n et b_{n + 1} = b_n.
  • si f(m_n) > k , on prend pour I_n+1 l'intervalle [a_n ; m_n]et on pose a_{n + 1} = a_n et b_{n + 1} = m_n..
  • si f(m_n) = k , on s'arrête.

Deux cas se présentent :

• ou bien la suite est finie et il existe n tel que f(m_n) = k ; le problème est alors résolu, et on peut prendre : c = m_n
• ou bien la suite est infinie.

Dans ce cas, les suites (a_n) et (b_n) sont adjacentes : en effet, la première est croissante (au sens large), la seconde est décroissante, et la différence entre les deux suites est égale à la longueur de I_n,soit qui tend vers 0.

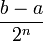
Ces deux suites convergent donc vers une même limite c. Comme f est continue, les suites (f(a_n)) et (f(b_n)) convergent vers f(c).

Comme, d'autre part, f(a_n) < k pour tout n, on obtient f(c) ≤ k par passage à la limite.

Comme, enfin, f(b_n) > k pour tout n, on obtient f(c) ≥ k par passage à la limite.

Il en résulte que f(c) = k.

Autres algorithmes

La dichotomie est un algorithme simple pour déterminer une valeur de c, mais n'est pas le plus performant: la précision n'augmente que d'un facteur 2 à chaque itération. On a donc cherché d'autres algorithmes permettant une convergence plus rapide. La méthode de Newton ou méthode des tangentes en est un d'une bonne efficacité.

• Article détaillé : Algorithme de recherche d'un zéro d'une fonction

Unicité de la solution

La méthode de dichotomie permet seulement de trouver l'une des solutions ; le fait d'éliminer tout un intervalle à chaque étape risque d'éliminer d'autres solutions.