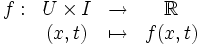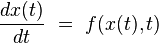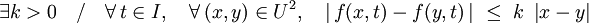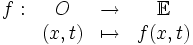Théorème de Cauchy-Lipschitz - Définition

Le théorème de Cauchy-Lipschitz assure l'existence locale et l'unicité de la solution d'une équation différentielle. Énoncé par Augustin Louis Cauchy en 1820, c'est Rudolf Lipschitz qui lui donnera sa forme définitive en 1868. Dans de nombreux pays, l'appellation la plus courante est celle de théorème de Picard-Lindelöf, du nom des mathématiciens Émile Picard et Ernst Lindelöf.

Théorème

Énoncé élémentaire

Soit f une fonction de deux variables réelles à valeurs réelles :

où est un intervalle de la droite réelle, et un autre intervalle de cette même droite. Considérons l'équation différentielle du premier ordre^[1] :

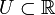
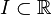
On suppose de plus que l'équation différentielle est soumise à la condition initiale : , où et .

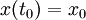
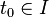
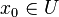
Si la fonction f est continue et k--Lipschitzienne en x, i.e. si f vérifie la condition de Lipschitz :

0 \quad / \quad \forall \, t \in I , \quad \forall \, (x,y) \in U^2 , \quad \left| \, f(x,t) - f(y,t) \, \right| \ \le \ k \ \left| x - y \right|" />

alors il existe une et une seule solution x(t) de l'équation différentielle définie pour tout , étant un intervalle centré sur t₀, vérifiant la condition initiale donnée.

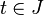
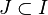
Ce théorème est à rapprocher de la notion de déterminisme en physique classique: si un système suit une loi d'évolution donnée (l'équation différentielle), les mêmes causes (les conditions initiales) produisent les mêmes effets.

Remarque

Le théorème de Cauchy-Lipschitz fournit une existence locale : il existe une et une seule solution x(t) qui n'est définie a priori que pour des instants t situés dans un intervalle J centré sur t₀. La question du prolongement maximal de cette solution, i.e. de son existence globale, se traite bien dans le cadre de l'étude des équations différentielles pour des temps t complexes. Ce prolongement maximal est lié à la présence de singularités. On doit notamment à Paul Painlevé d'importantes contributions à ce sujet^[2].

Énoncé général

Soit E un espace de Banach ^[3] de dimension finie sur ?, O un ouvert de E x ?, f une application de O dans E:

continue sur O et localement lipschitzienne en la première variable sur O, i.e. la fonction f vérifie la condition de Lipschitz :

où k est une constante. Considérons l'équation différentielle du premier ordre :

Alors^[4] :

• les solutions maximales de l'équation diférentielle sont définies sur des intervalles ouverts de ? ;

• les graphes des solutions maximales forment une partition de O ;

• toute solution de l'équation différentielle est la restriction d'une et d'une seule solution maximale de l'équation.

Extension aux équations aux dérivées partielles

Le théorème de Cauchy-Lipschitz assurant l'existence et l'unicité de la solution d'une équation différentielle admet une extension aux équations aux dérivées partielles : le théorème de Cauchy-Kovalevskaïa.