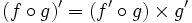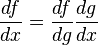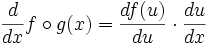Règle de dérivation en chaîne - Définition

En mathématiques, dans le domaine de l'analyse, la règle de dérivation en chaîne est le nom donné par les anglo-saxons à la formule de dérivation des fonctions composées.

Soient deux fonctions dérivables f,g alors leur composée qui est l'application qui à x associe f(g(x)) est dérivable et la dérivée de est donnée par

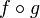
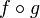
Il est aussi possible de l'écrire avec la notation de Leibniz sous la forme:

où indique que f dépends de g comme si g était une variable.

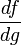
Pour une meilleure lecture on pose souvent et on obtient :

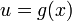
Applications

C'est de cette règle que découle la règle du changement de variable pour le calcul d'intégrales.